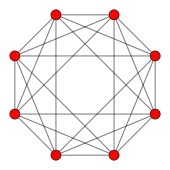
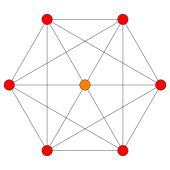
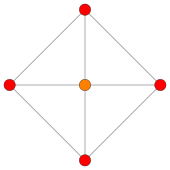
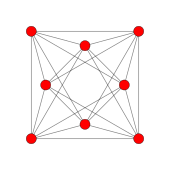
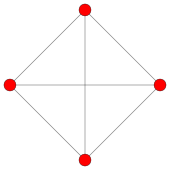
Шестнадцатиячейник
| Шестнадцатиячейник | |
|---|---|
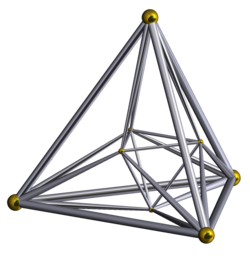 Диаграмма Шлегеля: проекция (перспектива) шестнадцатиячейника в трёхмерное пространство | |
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {3,3,4} |
| Ячеек | 16 |
| Граней | 32 |
| Рёбер | 24 |
| Вершин | 8 |
| Вершинная фигура | Правильный октаэдр |
| Двойственный политоп | Тессеракт |

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник[1] — один из шести правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб[2] (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.
Открыт Людвигом Шлефли в середине 1850-х годов[3]. Символ Шлефли шестнадцатиячейника — {3,3,4}.
Описание
Ограничен 16 трёхмерными ячейками — одинаковыми правильными тетраэдрами. Угол между двумя смежными ячейками равен в точности [math]\displaystyle{ 120^\circ. }[/math]
Его 32 двумерных грани — одинаковые правильные треугольники. Каждая грань разделяет 2 примыкающие к ней ячейки.
Имеет 24 ребра равной длины. На каждом ребре сходятся по 4 грани и по 4 ячейки.
Имеет 8 вершин. В каждой вершине сходятся по 6 рёбер, по 12 граней и по 8 ячеек. Любая вершина соединена ребром с любой другой — кроме вершины, симметричной ей относительно центра многоячейника.
Шестнадцатиячейник можно представить как две одинаковых правильных октаэдрических пирамиды, приложенные друг к другу своими основаниями, — либо как четырёхмерную дуопирамиду[англ.], построенную на двух квадратах.
В координатах
Шестнадцатиячейник можно расположить в декартовой системе координат так, чтобы его 8 вершин имели координаты [math]\displaystyle{ (\pm1;0;0;0), }[/math] [math]\displaystyle{ (0;\pm1;0;0), }[/math] [math]\displaystyle{ (0;0;\pm1;0), }[/math] [math]\displaystyle{ (0;0;0;\pm1). }[/math]
При этом сечения многоячейника 6 координатными плоскостями будут представлять собой 6 квадратов, вершины и рёбра которых — соответственно вершины и рёбра многоячейника.
Каждая из 16 ячеек многоячейника будет располагаться в одном из 16 ортантов четырёхмерного пространства.
Начало координат [math]\displaystyle{ (0;0;0;0) }[/math] будет центром симметрии шестнадцатиячейника, а также центром его вписанной, описанной и полувписанных трёхмерных гиперсфер.
Поверхность шестнадцатиячейника при этом будет геометрическим местом точек [math]\displaystyle{ (x;y;z;w), }[/math] чьи координаты удовлетворяют уравнению
- [math]\displaystyle{ |x|+|y|+|z|+|w|=1, }[/math]
а внутренность многоячейника — геометрическим место точек, для которых
- [math]\displaystyle{ |x|+|y|+|z|+|w|\lt 1. }[/math]
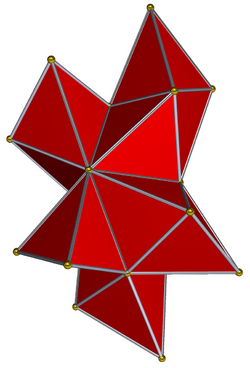
Ортогональные проекции на плоскость
Метрические характеристики
Если шестнадцатиячейник имеет ребро длины [math]\displaystyle{ a, }[/math] то его четырёхмерный гиперобъём и трёхмерная гиперплощадь поверхности выражаются соответственно как
- [math]\displaystyle{ V_4 = \frac{1}{6}\;a^4 \approx 0{,}1666667a^4, }[/math]
- [math]\displaystyle{ S_3 = \frac{4\sqrt{2}}{3}\;a^3 \approx 1{,}8856181a^3. }[/math]
Радиус описанной трёхмерной гиперсферы (проходящей через все вершины многоячейника) при этом будет равен
- [math]\displaystyle{ R = \frac{\sqrt{2}}{2}\;a \approx 0{,}7071068a, }[/math]
радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —
- [math]\displaystyle{ \rho_1 = \frac{1}{2}\;a = 0{,}5000000a, }[/math]
радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —
- [math]\displaystyle{ \rho_2 = \frac{\sqrt{6}}{6}\;a \approx 0{,}4082483a, }[/math]
радиус вписанной гиперсферы (касающейся всех ячеек в их центрах) —
- [math]\displaystyle{ r = \frac{\sqrt{2}}{4}\;a \approx 0{,}3535534a. }[/math]
Заполнение пространства
Шестнадцатиячейниками можно замостить четырёхмерное пространство без промежутков и наложений.
Примечания
- ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Е. Ю. Смирнов. Группы отражений и правильные многогранники. — М.: МЦНМО, 2009. — С. 44.
- ↑ George Olshevsky. Hexadecachoron // Glossary for Hyperspace.
Ссылки
- Weisstein, Eric W. Шестнадцатиячейник (англ.) на сайте Wolfram MathWorld.