Антипризма
Внешний вид
| Антипризма на [math]\displaystyle{ n }[/math]-угольнике | |||
|---|---|---|---|
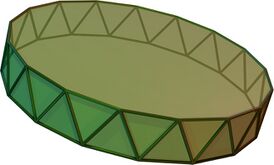 Антипризма на 17-угольнике Антипризма на 17-угольнике | |||
| Тип | полуправильный многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | [math]\displaystyle{ 2n }[/math] треугольников, 2 [math]\displaystyle{ n }[/math]-угольника | ||
| Конфигурация вершины | 3.3.3.[math]\displaystyle{ n }[/math] | ||
| Двойственный многогранник | трапецоэдр | ||
| Классификация | |||
| Обозначения | [math]\displaystyle{ A_n }[/math] | ||
| Символ Шлефли |
|
||
| Диаграмма Дынкина |
|
||
| Группа симметрии | [math]\displaystyle{ D_{nd} }[/math] | ||
| Группа вращения | [math]\displaystyle{ D_{n} }[/math] | ||
| Количественные данные | |||
| Длина ребра | [math]\displaystyle{ a }[/math] | ||
| Площадь поверхности | [math]\displaystyle{ \frac{n}{2} \left(\mathrm{ctg}{\frac{\pi}{n}} + \sqrt{3}\right) a^2 }[/math] | ||
| Объём | [math]\displaystyle{ \frac{n \sqrt{4\cos^2\frac{\pi}{2n}-1}\sin \frac{3\pi}{2n} }{12\sin^2\frac{\pi}{n}} \; a^3 }[/math] | ||
Антипризма — полуправильный многогранник, у которого две параллельные грани (основания) — равные между собой правильные n-угольники, а остальные 2n граней (боковые грани) — правильные треугольники.
Октаэдр является антипризмой с треугольными основаниями. Икосаэдр сложен из пятиугольной антипризмы и двух правильных пятиугольных пирамид.
Объем и площадь поверхности
Пусть [math]\displaystyle{ a }[/math] — длина ребра правильной антипризмы. Тогда её объем вычисляется по формуле:
- [math]\displaystyle{ V = \frac{n \sqrt{4\cos^2\frac{\pi}{2n}-1}\sin \frac{3\pi}{2n} }{12\sin^2\frac{\pi}{n}} \; a^3 }[/math]
а площадь поверхности по формуле:
- [math]\displaystyle{ S = \frac{n}{2} \left(\mathrm{ctg}{\frac{\pi}{n}} + \sqrt{3}\right) a^2. }[/math]
Вариации и обобщения

- Скрученная квадратная антипризма получается из антипризмы поворотом одного из оснований при сохранении комбинаторной структуры граней рёбер и вершин.
- Многогранник Шёнхардта — скрученная треугольная антипризма.
Шаблон:Однородные антипризмы Шаблон:Шестиугольные правильные мозаики
См. также
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |
