Скрученно удлинённая пятиугольная пирамида
| Скрученно удлинённая пятиугольная пирамида | |||
|---|---|---|---|
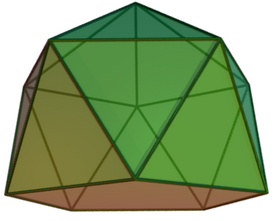 (3D-модель) (3D-модель) | |||
| Тип | многогранник Джонсона | ||
| Свойства | выпуклая | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
15 треугольников 1 пятиугольник |
||
| Конфигурация вершины |
5(33.5) 1+5(35) |
||
| Классификация | |||
| Обозначения | J11, М3+А5 | ||
| Группа симметрии | C5v | ||
Скру́ченно удлинённая пятиуго́льная пирами́да,[1] или отсечённый икоса́эдр — один из многогранников Джонсона (J11, по Залгаллеру — М3+А5).
Составлена из 16 граней: 15 правильных треугольников и 1 правильного пятиугольника. Пятиугольная грань окружена пятью треугольными; среди треугольных 5 граней окружены пятиугольной и двумя треугольными, другие 10 — тремя треугольными.
Имеет 25 рёбер одинаковой длины. 5 рёбер располагаются между пятиугольной и треугольной гранями, остальные 20 — между двумя треугольными.
У скрученно удлинённой пятиугольной пирамиды 11 вершин. В 5 вершинах сходятся пятиугольная грань и три треугольных; в остальных 6 — пять треугольных.
Скрученно удлинённую пятиугольную пирамиду можно получить из правильной пятиугольной пирамиды (J2) и правильной пятиугольной антипризмы, все рёбра у которых одинаковой длины, — приложив основание пирамиды к одному из оснований антипризмы.
Кроме того, скрученно удлинённую пятиугольную пирамиду можно получить из икосаэдра, отсекши от того пятиугольную пирамиду. Вершины полученного многогранника — 11 из 12 вершин икосаэдра, рёбра — 25 из 30 рёбер икосаэдра; отсюда ясно, что у скрученно удлинённой пятиугольной пирамиды тоже существуют описанная и полувписанная сферы, причём они совпадают с описанной и полувписанной сферами исходного икосаэдра.
Метрические характеристики
Если скрученно удлинённая пятиугольная пирамида имеет ребро длины [math]\displaystyle{ a }[/math], её площадь поверхности и объём выражаются как
- [math]\displaystyle{ S = \frac{1}{4}\left(15\sqrt3+\sqrt{25+10\sqrt5}\right)a^2 \approx 8{,}2156679a^2, }[/math]
- [math]\displaystyle{ V = \frac{1}{24}\left(25+9\sqrt5\right)a^3 \approx 1{,}8801922a^3. }[/math]
Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен
- [math]\displaystyle{ R = \frac{1}{4}\sqrt{10+2\sqrt5}\;a \approx 0{,}9510565a; }[/math]
радиус полувписанной сферы (касающейся всех рёбер в их серединах) —
- [math]\displaystyle{ \rho = \frac{1}{4}\left(1+\sqrt5\right)a \approx 0{,}8090170a. }[/math]
Примечания
- ↑ Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 20.
Ссылки
- Weisstein, Eric W. Скрученно удлинённая пятиугольная пирамида (англ.) на сайте Wolfram MathWorld.
