Трижды наращённая шестиугольная призма
| Трижды наращённая шестиугольная призма | |||
|---|---|---|---|
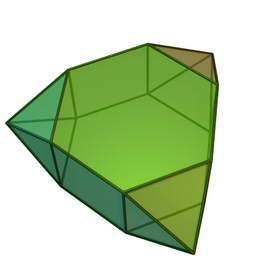 (3D-модель) (3D-модель) | |||
| Тип | многогранник Джонсона | ||
| Свойства | выпуклая | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
12 треугольников 3 квадрата 2 шестиугольника |
||
| Конфигурация вершины |
3(34) 12(32.4.6) |
||
| Классификация | |||
| Обозначения | J57, П6+3М2 | ||
| Группа симметрии | D3h | ||
Три́жды наращённая шестиуго́льная при́зма[1] — один из многогранников Джонсона (J57, по Залгаллеру — П6+3М2).
Составлена из 17 граней: 12 правильных треугольников, 3 квадратов и 2 правильных шестиугольников. Каждая шестиугольная грань окружена тремя квадратными и тремя треугольными; каждая квадратная грань окружена двумя шестиугольными и двумя треугольными; среди треугольных граней 6 окружены шестиугольной и двумя треугольными, другие 6 — квадратной и двумя треугольными.
Имеет 30 рёбер одинаковой длины. 6 рёбер располагаются между шестиугольной и квадратной гранями, 6 рёбер — между шестиугольной и треугольной, 6 рёбер — между квадратной и треугольной, остальные 12 — между двумя треугольными.
У трижды наращённой шестиугольной призмы 15 вершин. В 12 вершинах сходятся шестиугольная, квадратная и две треугольных грани; в 3 вершинах — четыре треугольных.
Трижды наращённую шестиугольную призму можно получить из четырёх многогранников — трёх квадратных пирамид (J1) и правильной шестиугольной призмы, все рёбра у которых одинаковой длины, — приложив основания пирамид к трём попарно не смежным квадратным граням призмы.
Метрические характеристики
Если трижды наращённая шестиугольная призма имеет ребро длины [math]\displaystyle{ a }[/math], её площадь поверхности и объём выражаются как
- [math]\displaystyle{ S = \left(3+6\sqrt3\right)a^2 \approx 13{,}3923048a^2, }[/math]
- [math]\displaystyle{ V = \frac{1}{2}\left(\sqrt2+3\sqrt3\right)a^3 \approx 3{,}3051830a^3. }[/math]
В координатах
Трижды наращённую шестиугольную призму с длиной ребра [math]\displaystyle{ 2 }[/math] можно расположить в декартовой системе координат так, чтобы её вершины имели координаты
- [math]\displaystyle{ \left(\pm1;\;\pm1;\;\pm\sqrt3\right), }[/math]
- [math]\displaystyle{ \left(\pm2;\;\pm1;\;0\right), }[/math]
- [math]\displaystyle{ \left(0;\;0;\;\sqrt2+\sqrt3\right), }[/math]
- [math]\displaystyle{ \left(\pm\frac{3+\sqrt6}{2};\;0;\;-\frac{\sqrt2+\sqrt3}{2}\right). }[/math]
При этом одна из четырёх осей симметрии многогранника будет совпадать с осью Oy, а две из четырёх плоскостей симметрии — с плоскостями xOz и yOz.
Примечания
- ↑ Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 22.
Ссылки
- Weisstein, Eric W. Трижды наращённая шестиугольная призма (англ.) на сайте Wolfram MathWorld.
