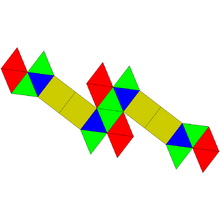
Опоясанный двуклинник
| Опоясанный двуклинник | |||
|---|---|---|---|
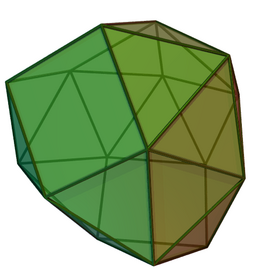 (3D-модель) (3D-модель) | |||
| Тип | многогранник Джонсона | ||
| Свойства | выпуклый | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
20 треугольников 4 квадрата |
||
| Конфигурация вершины |
4(32.42) 4(35) 8(34.4) |
||
| Классификация | |||
| Обозначения | J90, М24 | ||
| Группа симметрии | D2d | ||
Опоя́санный двукли́нник[1][2] — один из многогранников Джонсона (J90, по Залгаллеру — М24).
Составлен из 24 граней: 20 правильных треугольников и 4 квадратов. Каждая квадратная грань окружена квадратной и тремя треугольными; среди треугольных граней 12 окружены квадратной и двумя треугольными, остальные 8 — тремя треугольными.
Имеет 38 рёбер одинаковой длины. 2 ребра располагаются между двумя квадратными гранями, 12 рёбер — между квадратной и треугольной, остальные 24 — между двумя треугольными.
У опоясанного двуклинника 16 вершин. В 4 вершинах сходятся две квадратных грани и две треугольных; в 8 вершинах — квадратная и четыре треугольных; в остальных 4 — пять треугольных.
Метрические характеристики
Если опоясанный двуклинник имеет ребро длины [math]\displaystyle{ a }[/math], его площадь поверхности и объём выражаются как
- [math]\displaystyle{ S = \left(4+5\sqrt3\right)a^2 \approx 12{,}6602540a^2, }[/math]
- [math]\displaystyle{ V \approx 3{,}77763a^3. }[/math]
В координатах
Опоясанный двуклинник с длиной ребра [math]\displaystyle{ 2 }[/math] можно расположить в декартовой системе координат так, чтобы его вершины имели координаты[2]
- [math]\displaystyle{ \left(\pm1;\;0;\;2\sqrt{1-\xi^2}+\frac{\sqrt{2+8\xi-8\xi^2}}{2}\right), }[/math]
- [math]\displaystyle{ \left(\pm1;\;\pm2\xi;\;\frac{\sqrt{2+8\xi-8\xi^2}}{2}\right), }[/math]
- [math]\displaystyle{ \left(\pm\left(1+\sqrt{\frac{3-4\xi^2}{1-\xi^2}}\right);\;0;\;\frac{1-2\xi^2}{\sqrt{1-\xi^2}}+\frac{\sqrt{2+8\xi-8\xi^2}}{2}\right), }[/math]
- [math]\displaystyle{ \left(0;\;\pm\left(1+\sqrt{\frac{3-4\xi^2}{1-\xi^2}}\right);\;-\frac{1-2\xi^2}{\sqrt{1-\xi^2}}-\frac{\sqrt{2+8\xi-8\xi^2}}{2} \right), }[/math]
- [math]\displaystyle{ \left(\pm2\xi;\;\pm1;\;-\frac{\sqrt{2+8\xi-8\xi^2}}{2}\right), }[/math]
- [math]\displaystyle{ \left(0;\;\pm1;\;-2\sqrt{1-\xi^2}-\frac{\sqrt{2+8\xi-8\xi^2}}{2}\right), }[/math]
где [math]\displaystyle{ \xi \approx 0{,}7671311 }[/math] — четвёртый по величине после наибольшего[3] действительный корень уравнения
[math]\displaystyle{ 256x^{12}-512x^{11}-1664x^{10}+3712x^9+1552x^8-6592x^7+1248x^6+4352x^5-2024x^4-944x^3+672x^2-24x-23=0. }[/math]
При этом две оси симметрии многогранника будет совпадать с биссектрисами координатных углов плоскости xOy, а две плоскости симметрии — с плоскостями xOz и yOz.
Примечания
- ↑ Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 24.
- ↑ 2,0 2,1 А. В. Тимофеенко. Несоставные многогранники, отличные от тел Платона и Архимеда. (PDF) Фундаментальная и прикладная математика, 2008, том 14, выпуск 2. — Стр. 197—198. (Архивная копия от 30 августа 2021 на Wayback Machine)
- ↑ См. корни данного уравнения.
Ссылки
- Weisstein, Eric W. Опоясанный двуклинник (англ.) на сайте Wolfram MathWorld.
- Опоясанный двуклинник в базе знаний Wolfram Alpha