Перейти к содержанию

Пятнадцатиугольник

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Пятнадцатиугольник
Правильный пятнандцатиугольникПравильный пятнандцатиугольник
Тип Правильный многоугольник
Рёбра 15
Символ Шлефли {15}
Диаграмма Коксетера — Дынкина
Вид симметрии Диэдрическая группа (D15)
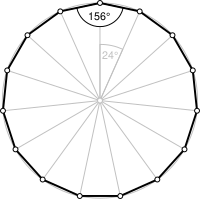
Внутренний угол 156°
Свойства
выпуклый, вписанный, Равносторонний, равноугольный[англ.], изотоксальный

Пятнадцатиугольник — это многоугольник с пятнадцатью сторонами.

Правильный пятнадцатиугольник

Правильный пятнадцатиугольник представлен символом Шлефли {15}.

Правильный пятнадцатиугольник имеет внутренние углы 156°. Со стороной a пятнадцатиугольник имеет площадь, задаваемую формулой

[math]\displaystyle{ \begin{align} A = \frac{15}{4}a^2 \mathrm{ctg}\, \frac{\pi}{15} & = \frac{15}{4}\sqrt{7+2\sqrt{5}+2\sqrt{15+6\sqrt{5}}}a^2 \\ & = \frac{15a^2}{8} \left( \sqrt{3}+\sqrt{15}+ \sqrt{2}\sqrt{5+\sqrt{5}} \right) \\ & \simeq 17.642362910544204\,a^2. \end{align} }[/math]

Использование


Правильный треугольник, десятиугольник и пятнадцатиугольник могут полностью закрыть вершину на плоскости.

Построение

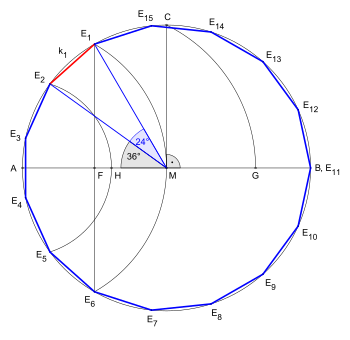
Поскольку 15 = 3 × 5 является произведением различных простых чисел Ферма, правильный пятнадцатиугольник можно построить с помощью циркуля и линейки: Следующие построения правильного пятнадцатиугольника с заданной описывающей окружностью аналогично иллюстрации для утверждения XVI в книге IV Начал Евклида[1].

Сравнение построения с построением Евклида см. на рисунке Пятнадцатиугольник

В построении для заданной описывающей окружности: [math]\displaystyle{ \overline{FG} = \overline{CF}\text{,} \; \overline{AH} = \overline{GM}\text{,} \; |E_1E_6| }[/math] равна стороне равностороннего треугольника, а [math]\displaystyle{ |E_2E_5| }[/math] равна стороне правильного пятиугольника[2]. Точка [math]\displaystyle{ H }[/math] делит радиус [math]\displaystyle{ \overline{AM} }[/math] в пропорции золотого сечения: [math]\displaystyle{ \frac{\overline{AH}}{\overline{HM}} = \frac{\overline{AM}}{\overline{AH}} = \frac{1+ \sqrt{5}}{2} = \Phi \approx 1,618 \text{.} }[/math]

Сравнение с первой анимацией (с зелёными прямыми) приведено на следующих двух рисунках. Две дуги (для углов 36° и 24°) смещены против часовой стрелки. Построение не использует отрезок [math]\displaystyle{ \overline{CG} }[/math], а вместо него использует отрезок [math]\displaystyle{ \overline{MG} }[/math] как радиус [math]\displaystyle{ \overline{AH} }[/math] для второй дуги (угол 36°).

01-Fünfzehneck01-FünfzehneckAnimation

Построение с помощью циркуля и линейки для заданной длины стороны. Построение почти такое же, что и для построения пятиугольника по заданной стороне, оно также начинается с создания отрезка как продолжения стороны, здесь [math]\displaystyle{ \overline{FE_2}\text{,} }[/math], который делится в пропорции золотого сечения:

[math]\displaystyle{ \frac{\overline{E_1 E_2}}{\overline{E_1 F}} = \frac{\overline{E_2 F}}{\overline{E_1 E_2}} = \frac{1+ \sqrt{5}}{2} = \Phi \approx 1.618033988749895 \text{.} }[/math]

Радиус описанной окружности [math]\displaystyle{ \overline{E_2 M} = R\;;\;\; }[/math]
Длина стороны [math]\displaystyle{ \overline{E_1 E_2} = a\;;\;\; }[/math]
Угол [math]\displaystyle{ D E_1M = ME_2D = 78^\circ }[/math]

[math]\displaystyle{ \begin{align} R &= a \cdot \frac{1}{2} \cdot \left(\sqrt{5 + 2 \cdot \sqrt{5}} + \sqrt{3} \right)= \frac{1}{2} \cdot \sqrt{8+ 2 \cdot \sqrt{5}+2\sqrt{15 + 6 \cdot \sqrt{5}}}\cdot a\\ &= \frac {\sin (78^\circ)}{ \sin (24^\circ)} \cdot a \approx 2.4048671723720654\cdot a \end{align} }[/math]

Симметрия

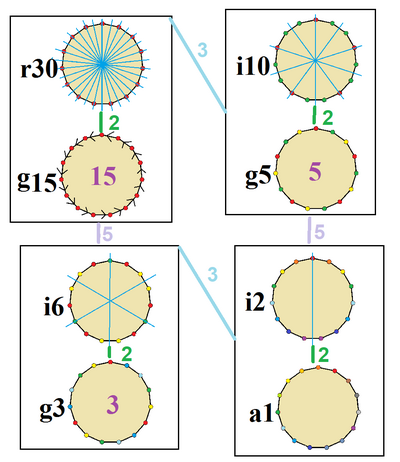
Симметрии правильного пятнадцатиугольника показаны цветом на рёбрах и вершинах. Прямые отражений показаны синим цветом. Вращения задаются числами в центре. Вершины выкрашены согласно симметрии.

Правильный пятнадцатиугольник имеет диэдральную симметрию порядка 30 (Dih15), представленную 15 прямыми зеркального отражения. Dih15 имеет 3 диэдральные подгруппы: Dih5, Dih3 и Dih1. А кроме того, ещё четыре циклические симметрии — Z15, Z5, Z3 и Z1, где Zn представляет π/n вращательную симметрию.

В пятнадцатиугольнике имеется 8 различных симметрий. Джон Конвей обозначил симметрии буквами с указанием порядка симметрии после буквы[3]. Он обозначил через r30 полную симметрию отражений Dih15, обозначил через d (diagonal = диагональ) отражения относительно прямых, проходящих через вершины, через p отражения относительно прямых, проходящих через середины рёбер (perpendicular = перпендикуляр), а для пятнадцатиугольника с нечётным числом вершин использовал букву i (для зеркал через вершину и середину ребра) и букву g для циклической симметрии. Символ a1 означает отсутствие симметрии.

Эти низкие степени симметрий определяют степени свободы в определении неправильных пятнадцатиугольников. Только подгруппа g15 не имеет степеней свободы, но может рассматриваться как обладающая ориентированными рёбрами.

Пентадекаграммы

Существует три правильных звезды: {15/2}, {15/4}, {15/7} на тех же самых 15 вершинах правильного пятнадцатиугольника, но соединённых через одну, через три или через шесть вершин.

Есть также три правильных звёздчатых фигуры[англ.]: {15/3}, {15/5}, {15/6}, первая состоит из трёх пятиугольников, вторая состоит из пяти правильных треугольников, а третья состоит из трёх пентаграмм.

Составную фигуру {15/3} можно рассматривать как двухмерный эквивалент трёхмерного соединения пяти тетраэдров.

Picture
{15/2}
{15/3} or 3{5}
{15/4}
{15/5} or 5{3}
{15/6} or 3{5/2}
{15/7}
Внутренний угол[англ.] 132° 108° 84° 60° 36° 12°

Более глубокие усечения правильного пятнадцатиугольника и пентадекаграмм могут дать изогональные (вершинно транзитивные) промежуточные звёздчатые многоугольники, образованные вершинами, находящимися на одинаковом расстоянии, и двумя длинами рёбер[4].

Вершинно транзитивные функции на пятнадцатиугольнике
Квазирегулярные Равноугольные Квазирегулярные

t{15/2}={30/2}
t{15/13}={30/13}

t{15/7} = {30/7}
t{15/8}={30/8}

t{15/11}={30/22}
t{15/4}={30/4}

Многоугольники Петри

Правильный пятнадцатиугольник является многоугольником Петри для некоторого многогранника высокой размерности, полученного ортогональной проекцией:


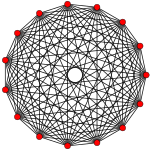14-симплекс (14D)

Он также является многоугольником Петри для большого 120-ячейника[англ.] и великого звёздчатого 120-ячейника[англ.].

Примечания

  1. ↑ Dunham, 1991, с. 65.
  2. ↑ Kepler, 1939, с. 44.
  3. ↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 275-278.
  4. ↑ Grünbaum, 1994.

Литература

  • William Dunham. Journey through Genius - The Great Theorems of Mathematics. — Penguin, 1991. the University of Kentucky College of Arts & Sciences Mathematics
  • Johannes Kepler. WELT-HARMONIK / translated and initiated by MAX CASPAR 1939. — Google Books, 1939.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // . — The Symmetries of Things, 2008. — ISBN 978-1-56881-220-5.
  • Branko Grünbaum. Metamorphoses of polygons // The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History. — 1994.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Пятнадцатиугольник&oldid=5899949