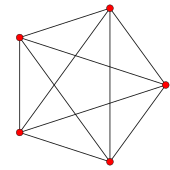
Пятиячейник
| Пятиячейник | |
|---|---|
 Диаграмма Шлегеля: проекция (перспектива) пятиячейника в трёхмерное пространство | |
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {3,3,3} |
| Ячеек | 5 |
| Граней | 10 |
| Рёбер | 10 |
| Вершин | 5 |
| Вершинная фигура | Правильный тетраэдр |
| Двойственный политоп | Он же (самодвойственный) |

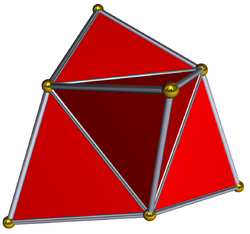
Пра́вильный пятияче́йник, или просто пятияче́йник[1], или пентахор (от др.-греч. πέντε — «пять» и χώρος — «место, пространство»), — один из шести правильных многоячейников в четырёхмерном пространстве: правильный четырёхмерный симплекс.
Открыт Людвигом Шлефли в середине 1850-х годов[2]. Символ Шлефли пятиячейника — {3,3,3}.
Двойственен сам себе. В отличие от пяти других правильных многоячейников, не имеет центральной симметрии.
Используется в физико-химическом анализе для изучения свойств многокомпонентных систем[3].
Описание
Ограничен 5 трёхмерными ячейками — одинаковыми правильными тетраэдрами. Любые две ячейки — смежные; угол между ними равен [math]\displaystyle{ \arccos \, \frac{1}{4} \approx 75{,}52^\circ. }[/math]
Его 10 двумерных граней — одинаковые правильные треугольники. Каждая грань разделяет 2 примыкающие к ней ячейки.
Имеет 10 рёбер равной длины. На каждом ребре сходятся по 3 грани и по 3 ячейки.
Имеет 5 вершин. В каждой вершине сходятся по 4 ребра, по 6 граней и по 4 ячейки. Любые 2 вершины соединены ребром; любые 3 вершины принадлежат одной грани; любые 4 вершины принадлежат одной ячейке.
Пятиячейник можно рассматривать как правильную четырёхмерную пирамиду с тетраэдрическим основанием.
В координатах
Первый способ расположения
Пятиячейник можно разместить в декартовой системе координат так, чтобы его вершины имели координаты [math]\displaystyle{ (1;1;1;0), }[/math] [math]\displaystyle{ (1;-1;-1;0), }[/math] [math]\displaystyle{ (-1;1;-1;0), }[/math] [math]\displaystyle{ (-1;-1;1;0), }[/math] [math]\displaystyle{ (0;0;0;\sqrt5). }[/math]
При этом точка [math]\displaystyle{ \left(0;0;0;\frac{\sqrt5}{5}\right) }[/math] будет центром вписанной, описанной и полувписанных трёхмерных гиперсфер.
Второй способ расположения
Если разместить пятиячейник так, чтобы его вершины имели координаты [math]\displaystyle{ \left(\frac{\sqrt5}{4};\frac{\sqrt5}{4};\frac{\sqrt5}{4};\frac{1}{4}\right), }[/math] [math]\displaystyle{ \left(\frac{\sqrt5}{4};-\frac{\sqrt5}{4};-\frac{\sqrt5}{4};\frac{1}{4}\right), }[/math] [math]\displaystyle{ \left(-\frac{\sqrt5}{4};\frac{\sqrt5}{4};-\frac{\sqrt5}{4};\frac{1}{4}\right), }[/math] [math]\displaystyle{ \left(-\frac{\sqrt5}{4};-\frac{\sqrt5}{4};\frac{\sqrt5}{4};\frac{1}{4}\right), }[/math] [math]\displaystyle{ \left(0;0;0;-1\right), }[/math] то они будут лежать на гиперсфере радиуса [math]\displaystyle{ 1 }[/math] с центром в начале координат.
Третий способ расположения
В пятимерном пространстве возможно разместить пятиячейник так, чтобы все его вершины имели целые координаты: [math]\displaystyle{ (1;0;0;0;0), }[/math] [math]\displaystyle{ (0;1;0;0;0), }[/math] [math]\displaystyle{ (0;0;1;0;0), }[/math] [math]\displaystyle{ (0;0;0;1;0), }[/math] [math]\displaystyle{ (0;0;0;0;1). }[/math]
Центром вписанной, описанной и полувписанных гиперсфер при этом будет точка [math]\displaystyle{ \left(\frac{1}{5};\frac{1}{5};\frac{1}{5};\frac{1}{5};\frac{1}{5}\right). }[/math]
Ортогональные проекции на плоскость
Метрические характеристики
Если пятиячейник имеет ребро длины [math]\displaystyle{ a, }[/math] то его четырёхмерный гиперобъём и трёхмерная гиперплощадь поверхности выражаются соответственно как
- [math]\displaystyle{ V_4 = \frac{\sqrt5}{96}\;a^4\ \approx 0{,}0232924a^4, }[/math]
- [math]\displaystyle{ S_3 = \frac{5\sqrt2}{12}\;a^3 \approx 0{,}5892557a^3. }[/math]
Радиус описанной трёхмерной гиперсферы (проходящей через все вершины многоячейника) при этом будет равен
- [math]\displaystyle{ R = \frac{\sqrt{10}}{5}\;a \approx 0{,}6324555a, }[/math]
радиус внешней полувписанной гиперсферы (касающейся всех рёбер в их серединах) —
- [math]\displaystyle{ \rho_1 = \frac{\sqrt{15}}{10}\;a \approx 0{,}3872983a, }[/math]
радиус внутренней полувписанной гиперсферы (касающейся всех граней в их центрах) —
- [math]\displaystyle{ \rho_2 = \frac{\sqrt{15}}{15}\;a \approx 0{,}2581989a, }[/math]
радиус вписанной гиперсферы (касающейся всех ячеек в их центрах) —
- [math]\displaystyle{ r = \frac{\sqrt{10}}{20}\;a \approx 0{,}1581139a. }[/math]
Неправильные пятиячейники
Иногда словом «пятиячейник» может обозначаться не только правильный, но и произвольный четырёхмерный симплекс.
Примечания
- ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ George Olshevsky. Pentachoron // Glossary for Hyperspace.
- ↑ Александр Семёнов. Многогранный пентатоп // Наука и жизнь. — 2018. — № 5. — С. 66—74.
Ссылки
- Weisstein, Eric W. Пятиячейник (англ.) на сайте Wolfram MathWorld.