Гиперкуб

Гиперку́б — обобщение куба на случай с произвольным числом измерений.

Гиперкубом размерности Ν называется множество точек в Ν-мерном евклидовом пространстве, удовлетворяющее неравенствам [math]\displaystyle{ \forall i: -\frac{a}{2}\lt x_i\lt \frac{a}{2} }[/math], где [math]\displaystyle{ a }[/math] — длина ребра гиперкуба.

Также можно определить гиперкуб как декартово произведение Ν равных отрезков.

Также можно сказать, что Ν-куб — это фигура, каждая вершина которой связана рёбрами с Ν другими вершинами; Ν, в свою очередь, определяет размерность этой фигуры. Или же, Ν-мерный куб образуется Ν парами параллельных (Ν-1)-плоскостей, то есть имеет 2Ν гиперграни, каждая из которых является (Ν-1)-кубом.

В общем случае, число K‑мерных граней Ν‑мерного куба равно [math]\displaystyle{ {2}^{N-K}C_N^K }[/math], где [math]\displaystyle{ C_N^K }[/math] есть число групп K‑мерных параллельных граней (или число K‑мерных граней при одной вершине), [math]\displaystyle{ {2}^{N-K} }[/math] — число K‑мерных параллельных граней в группе.

Свойства гиперкуба

Свойство	Значение
Длина ребра	a
Размерность	N
Гиперобъём	[math]\displaystyle{ V_N = a^N }[/math]
Гиперплощадь поверхности	[math]\displaystyle{ S_N = 2Na^{N-1} }[/math]
Длина диагонали	[math]\displaystyle{ L_N = a\sqrt{N} }[/math]
Радиус описанной гиперсферы	[math]\displaystyle{ R = \frac{a\sqrt{N}}{2} }[/math]
Радиус вписанной гиперсферы	[math]\displaystyle{ r = \frac{a}{2} }[/math]

Различные гиперкубы

N-Куб	Изображение (двумерная проекция)	Название	Точек (0)	Отрезков (1)	Квадратов (2)	Кубов (3)	Тессерактов (4)	Пентерактов (5)	Хексерактов (6)	Хептерактов (7)	Октерактов (8)	Эннерактов (9)	Декерактов (10)
0-куб		Точка	1	0
1-куб		Отрезок	2	1	0
2-куб		Квадрат	4	4	1	0
3-куб		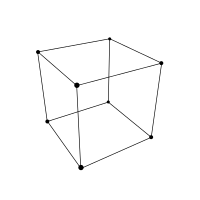Куб	8	12	6	1	0
4-куб		Тессеракт	16	32	24	8	1	0
5-куб		Пентеракт	32	80	80	40	10	1	0
6-куб		Гексеракт	64	192	240	160	60	12	1	0
7-куб		Гептеракт	128	448	672	560	280	84	14	1	0
8-куб		Октеракт	256	1024	1792	1792	1120	448	112	16	1	0
9-куб		Эннеракт	512	2304	4608	5376	4032	2016	672	144	18	1	0
10-куб		Декеракт	1024	5120	11520	15360	13440	8064	3360	960	180	20	1

Гиперкуб в художественной литературе

• Роберт Хайнлайн. «Дом, который построил Тил».
• Роберт Шекли. «Мисс Мышка и четвёртое измерение».
• Эдвин Эбботт. «Флатландия».
• Уолтер Тевис. «Новые измерения».

См. также

• Правильные N-мерные многогранники

Ссылки

• Анимация развёртки из квадрата до октеракта (и стереопара)
• Коксестер, Правильные политопы, (третье издание, 1973), Dover edition, ISBN 0-486-61480-8