Замощение (геометрия)

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.
Кроме паркетов на евклидовой плоскости, в математике рассматриваются «паркеты» на сфере, гиперболической плоскости, в трёхмерном и многомерном пространстве.
Терминология
Замощения, мозаики, паркеты, разбиения
Паркеты иначе называются замощениями, мозаиками (англ. tessellation, tiling), разбиениями плоскости (англ. partition), паркетажами. Замощения трёхмерного пространства и пространств высших размерностей часто называют со́тами.
На странице 16 книги Грюнбаума и Шепарда[англ.] «Tilings and Patterns» (1987)[2] находится следующее примечание:
В математической литературе слова tessellation, paving, mosaic и parquetting используются как синонимы или со сходными значениями. Немецкие слова для мозаики — Pflasterung, Felderung, Teilung, Parkettierung и Zerlegung; французские слова — pavage, carrelage и dallage; русские слова — паркетаж, разбиение и замощение.
Оригинальный текст (англ.)In mathematical literature, the words tessellation, paving, mosaic and parquetting are used synonymously or with similar meanings. The German words for tiling are Pflasterung, Felderung, Teilung, Parkettierung and Zerlegung. The French words are pavage, carrelage and dallage. The Russian words are паркетаж, разбиение and замощение.
Паркеты с областями (плитками) произвольной формы иногда называют картами (см., напр., теорема о четырёх красках).
Покрытия и упаковки
Если объединение нескольких фигур содержит данную фигуру Ф, то говорят, что эти фигуры образуют покрытие фигуры Ф. При этом покрывающие фигуры могут перекрываться, но покрывают фигуру Ф без пробелов.
Упаковка — это размещение внутри данной фигуры нескольких фигур, не имеющих общих точек, кроме, быть может, граничных (т.е. без перекрытий).
Замощение — это разбиение фигуры на части. Замощение является одновременно покрытием и упаковкой[2][3].
Протоплитки
Протоплитки паркета (англ. prototiles, также прототипы[4]) — это плитки (формы), входящие в паркет. Каждая плитка паркета конгруэнтна одной из протоплиток[5].
Так, единственная протоплитка шестиугольного паркета — правильный шестиугольник; протоплиткой правильного сферического пятиугольного паркета является пентагон; множество протоплиток ромботришестиугольного паркета состоит из равностороннего треугольника, квадрата и гексагона.
Паркет называется k-эдрическим, если множество его протоплиток (протомножество) состоит из k плиток[2][4].
Плитки паркета также называют гранями, а стороны многоугольных плиток — рёбрами, по аналогии с терминологией для многогранников[6].
Конфигурации вершин и граней
Ромботришестиугольный паркет[англ.] состоит из плиток трёх типов: равносторонний треугольник, квадрат и гексагон. Эти плитки располагаются вокруг каждой из вершин в следующем порядке: треугольник, квадрат, шестиугольник, квадрат. Такой порядок называется конфигурацией вершины паркета и записывается в форме 3.4.6.4. В случае, если два и более числа в этой последовательности идут подряд, используется сокращённая запись: треугольный паркет может быть обозначен как 3.3.3.3.3.3 или как 36. При этом записи, отличающиеся лишь циклической перестановкой чисел или изменением порядка записи на противоположный (например, 3.3.4.3.4 и 4.3.3.4.3), обозначают одну и ту же конфигурацию вершины; в то же время запись 3.4.4.6 не эквивалентна записи 3.4.6.4[4][7][8][9][10].
В неоднородных паркетах могут встречаться вершины с разными конфигурациями.
Конфигурацией грани называется последовательность степеней вершин этой грани при обходе её в одном направлении. Конфигурация грани записывается последовательностью чисел в квадратных скобках[2] или с префиксом V.
Если все вершины некоторого паркета имеют одну и ту же конфигурацию с записью a1.a2....ak, то все грани двойственного ему паркета имеют одну и ту же конфигурацию с записью Va1.a2....ak. Например, конфигурации граней паркета, двойственного ромботришестиугольному паркету 3.4.6.4 (англ.), записываются как V3.4.6.4.
Виды паркетов
Во многих случаях принимается условие эквивалентности каждой из протоплиток паркета топологическому диску; иными словами, плитка не должна состоять из нескольких частей (квазиполимино[11]), содержать «отверстия», быть бесконечной полосой и т.п.[2][4].
Паркеты на плоскости
Правильные паркеты
Паркеты, составленные из одинаковых правильных многоугольников, называют правильными паркетами (англ. regular tilings). Существует три правильных замощения плоскости: треугольный паркет, квадратный паркет и шестиугольный паркет[9][12][13].
- Правильные паркеты
Правильные паркеты называют также платоновыми паркетами[14].
Полиформы, располагающиеся на правильных паркетах, называются соответственно полиамондами, полимино и полигексами.
Для обозначения паркета из правильных p-угольников, расположенных по q вокруг каждой вершины, применяется символ Шлефли {p, q}. Символы Шлефли трёх правильных мозаик — {3,6}, {4,4} и {6,3}[6].
Полуправильные паркеты
Паркеты, состоящие из правильных многоугольников двух или более типов, такие, что для любых двух вершин паркета существует преобразование симметрии (самосовмещение), переводящее одну из них в другую, называются полуправильными паркетами (англ. semiregular tilings) или архимедовыми паркетами[9][15][16][17].
Существует 8 полуправильных паркетов[7][10][12][16][17]. Один из восьми полуправильных паркетов (курносый тришестиугольный паркет) является хиральным, то есть не совпадает с собственным зеркальным отражением[4][7][16][17].
- Полуправильные паркеты (Архимедовы паркеты)
-
Курносый квадратный паркет
3.3.4.3.4 -
Тришестиугольный паркет
3.6.3.6
Существует два определения, приводящих к одному и тому же набору из 8 полуправильных паркетов на плоскости.
Первое, «локальное» определение, заключается в том, что вершинные конфигурации всех вершин должны совпадать. Иными словами, последовательности граней вокруг любых двух вершин паркета должны быть одинаковыми: одни и те же многоугольники должны идти в одном и том же (или в противоположном) порядке.
Второе, «глобальное» определение, требует, чтобы для любых двух вершин паркета существовало преобразование симметрии (самосовмещение паркета), переводящее одну из них в другую.
Грюнбаум и Шепард разделяют термины «архимедов паркет» (англ. Archimedean tiling) и «однородный паркет» (англ. uniform tiling): к первой группе относятся паркеты, соответствующие «локальному» определению, а ко второй — «глобальному». Хотя на евклидовой плоскости два этих множества совпадают, в других пространствах существуют архимедовы паркеты, не являющиеся однородными[2].
В математической литературе значения терминов «архимедов паркет», «полуправильный паркет» и «однородный паркет» варьируются.
Квазиправильные паркеты
Квазиправильный паркет (или многогранник) (англ. quasiregular tiling) — однородный паркет (или многогранник), состоящий из граней двух видов, чередующихся вокруг каждой вершины; иными словами, каждая грань окружена гранями другого типа[18][19][20].
На евклидовой плоскости существует лишь один квазиправильный паркет — тришестиугольный паркет с вершинной конфигурацией 3.6.3.6. На сфере существует два квазиправильных паркета (сферических многогранника) — кубооктаэдр и икосододекаэдр.
На плоскости Лобачевского существует бесконечное множество квазиправильных паркетов вида [math]\displaystyle{ p.q.p.q, }[/math] где [math]\displaystyle{ \frac{1}{p}+\frac{1}{q}\lt \frac{1}{2}. }[/math]
Неоднородные паркеты
Существует бесконечное множество неоднородных (англ. non-uniform) паркетов, состоящих из правильных многоугольников.
- Неоднородные паркеты из правильных многоугольников
-
32.62, 36
-
32.62, 3.6.3.6
-
32.4.12, 36
-
3.42.6, 3.6.3.6
Периодические неоднородные паркеты можно классифицировать по числу орбит вершин, рёбер и граней. Если число орбит вершин равно n, паркет называется n-однородным (англ. n-uniform) или n-изогональным; если число орбит рёбер равно n — n-изотоксальным (англ. n-isotoxal). Вышеприведённые примеры представляют собой четыре из двадцати 2-однородных паркетов[2][9][21].
Непериодические паркеты и апериодические множества плиток



Разбиение T называется периодическим, если среди симметрий T существуют два параллельных переноса в непараллельных направлениях. В этом случае мозаику можно считать состоящей из повторений небольшого фрагмента, выложенного из элементов в узлах некоторой решётки. Множество прототипов (протомножество) P называется апериодическим, если оно реализуется в каких-то разбиениях плоскости, но ни одно из этих разбиений не является периодическим[4].
Первый пример апериодического множества плиток был найден Робертом Берджером[англ.] в 1966 году и включал в себя 20 426 плиток Вана[2][24]. Плитки Вана представляют собой квадраты одного размера с окрашенными сторонами; при построении мозаики разрешено совмещать плитки лишь одноцветными сторонами и запрещено переворачивать плитки.
Позднее были найдены апериодические протомножества с ме́ньшим числом плиток. Роджер Пенроуз обнаружил апериодические протомножества, состоящие из двух плиток[2][23][25].
В 2010 году Джошуа Соколар и Джон Тэйлор предложили апериодическое множество, состоящее из единственной плитки[англ.], которая представляет собой правильный шестиугольник с нанесённой разметкой в виде цветных линий и с дополнительными ограничениями, связанными с взаимным расположением не касающихся друг друга плиток[26]. Существует модификация, не использующая подобных ограничений, но использующая несвязную плитку, т.е., плитку, не являющуюся топологическим диском. Существование единственной связной плитки без дополнительной разметки и ограничений, способной покрыть плоскость только апериодически, остаётся открытой проблемой[26][27].

Паркеты в пространстве

Задача замощения может ставиться и решаться не только на плоскости, но и в трёхмерном пространстве и пространствах высших размерностей. В частности, примером замощения в трёхмерном пространстве являются кристаллы (если рассматривать их кристаллическую решётку не как центры атомов, а как тела, построенные вокруг этих центров и соприкасающиеся без зазоров и наложений - пространственные соты).
Сферические многогранники
Сферический паркет или сферический многогранник — разбиение сферы на сферические многоугольники дугами больших кругов[28].
Каждому из 5 платоновых тел соответствует правильный сферический паркет. Формально, пусть S — сфера с центром O, совпадающим с центром многогранника P. Проведённые из O лучи, проходящие через вершины многогранника P, пересекают сферу S в точках, являющихся вершинами соответствующего сферического паркета; рёбра многогранника P соответствуют дугам больших кругов на S.
Помимо сферических аналогов пяти «платоновых тел», существует два семейства правильных сферических многогранников, не имеющих эквивалентов среди многогранников с плоскими гранями: осоэдры — многогранники с двумя вершинами, находящимися на полюсах сферы, грани которых являются конгруэнтными двуугольниками, и диэдры — двойственные осоэдрам двугранники, вершины которых находятся на экваторе сферы.


Гиперболические паркеты
Аксиома параллельности Евклида (точнее, одно из эквивалентных ей утверждений) гласит:
Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.
В геометрии Лобачевского, вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Для изображения гиперболической плоскости применяется одна из существующих моделей — модель Бельтрами — Клейна, конформный диск Пуанкаре, модель Пуанкаре на полуплоскости[29].
На евклидовой плоскости существует лишь три правильных паркета и 8 полуправильных. На гиперболической плоскости существует бесконечное множество даже правильных паркетов, включая паркеты с семью и более равносторонними треугольниками вокруг вершины, пятью и более квадратами, четырьмя и более правильными пятиугольниками (паркет с тремя пятиугольниками вокруг вершины является сферическим додекаэдром), четырьмя и более правильными шестиугольниками и тремя и более равными правильными многоугольниками с количеством сторон более 6.
Задачи на паркетах
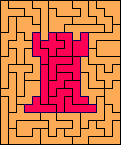
Большое количество задач и головоломок связано с разбиением прямоугольников (или других связных фигур) на плитки из определённого заданного множества протоплиток. Сами протоплитки при этом могут представлять собой связные объединения ячеек правильного паркета.
В частности, существует класс задач на замощение прямоугольников m × n плитками домино таким образом, чтобы в полученном разбиении не было прямой линии, пересекающей прямоугольник от края до края и не пересекающей ни одной плитки домино; такие прямоугольники называются «прочными»[4][11][30].
В других задачах устанавливается дополнительное ограничение на количество плиток каждого вида, используемых в замощении. В задачах, связанных с пентамино, требуется покрыть 12 фигурами заданное подмножество квадратного паркета, состоящее из 60 клеток (прямоугольники 3 × 20, 4 × 15, 5 × 12, 6 × 10, шахматная доска с вырезанным в центре квадратным тетрамино и др.); при этом каждая плитка должна быть использована ровно один раз[11][30].
Перечисление паркетов
Задача определения количества паркетов, состоящих из выпуклых многоугольников заданного типа, решена лишь частично:
- Любым треугольником или четырёхугольником можно замостить плоскость[4][31][32].
- Известно 15 пятиугольников, способных замостить плоскость; недавно французские учёные, открывшие 15 пятиугольник, доказали, что других таких нет.[1]. Проблема перечисления пятиугольных паркетов имеет богатую историю[4], и, возможно, уже решена[33][34].
- Известно 3 типа шестиугольников, способных замостить плоскость[4][35].
- Невозможно замостить плоскость одинаковыми выпуклыми многоугольниками с числом сторон, большим или равным семи[4][36].
См. также
- Диаграмма Вороного
- Триангуляция Делоне
- Мозаика Пенроуза
- Проблема четырёх красок
- Стереографическая проекция
- Замощение (компьютерная графика)
Примечания
- ↑ 1,0 1,1 Weisstein, Eric W. Pentagon Tiling (англ.) на сайте Wolfram MathWorld.
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 B. Grünbaum, G.C. Shephard. Tilings and Patterns. — New York: W. H. Freeman & Co., 1987. — ISBN 0-7167-1193-1.
- ↑ Как решают нестандартные задачи / Под ред. В. О. Бугаенко. — М.: МЦНМО, 2008. — С. 49. — 96 с. — ISBN 978-5-94057-331-9.
- ↑ 4,00 4,01 4,02 4,03 4,04 4,05 4,06 4,07 4,08 4,09 4,10 Дэвид А. Кларнер. Математический цветник.
- ↑ Prototile. Encyclopedia of Mathematics. Дата обращения: 12 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ 6,0 6,1 Кокстер, Введение в геометрию, 1966, §6, с. 100 — 104.
- ↑ 7,0 7,1 7,2 Henry Martyn Cundy, A. P. Rollett. Mathematical Models (англ.). — 2nd ed.. — Oxford University Press, 1961. — P. 59—65.
- ↑ Paul Bourke. Uniform Polyhedra. Дата обращения: 12 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ 9,0 9,1 9,2 9,3 Chavey, D. Tilings by Regular Polygons—II: A Catalog of Tilings (неопр.) // Computers and Mathematics with Applications. — 1989. — Т. 17. — С. 147—165. — doi:10.1016/0898-1221(89)90156-9.
- ↑ 10,0 10,1 What Is a Tessellation?. Math Forum. Дата обращения: 12 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ 11,0 11,1 11,2 Голомб С.В. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М.: Мир, 1975. — 207 с.
- ↑ 12,0 12,1 Энциклопедия для детей. Т. 11. Математика / Глав. ред. М. Д. Аксёнова; метод. и отв. ред. В. А. Володин. — М.: Аванта+, 2003. — С. 297—300. — 688 с. — ISBN 5-94623-072-7.
- ↑ Weisstein, Eric W. Regular Tessellation (англ.) на сайте Wolfram MathWorld.
- ↑ Steven Gillispie. The Platonic planar tilings. Архивировано 26 октября 2008 года.
- ↑ Weisstein, Eric W. Semiregular Tessellation (англ.) на сайте Wolfram MathWorld.
- ↑ 16,0 16,1 16,2 Steven Dutch. Archimedean Tilings (2 июля 1999). Архивировано 20 января 2013 года.
- ↑ 17,0 17,1 17,2 John Baez. Archimedean Tilings and Egyptian Fractions. Azimuth (5 февраля 2012). Дата обращения: 12 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ М. Веннинджер. Модели многогранников = Polyhedron Models / Перевод с английского В. В. Фирсова, под редакцией и с послесловием И. М. Яглома. — М.: Мир, 1974. — 236 с.
- ↑ George Hart. Quasiregular Polyhedra. Virtual Polyhedra: The Encyclopedia of Polyhedra. Дата обращения: 19 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ H. S. M. Coxeter. Regular Polytopes (англ.). — 1973. — ISBN 0-486-61480-8.
- ↑ Steven Dutch. Uniform Tilings (2 июля 1999). Архивировано 20 января 2013 года.
- ↑ Penrose R. (1979/80), Pentaplexity, Math. Intell. Т. 2: 32–37, <http://www.ma.utexas.edu/users/radin/pentaplexity.html> Архивная копия от 7 июня 2011 на Wayback Machine(archived at)
- ↑ 23,0 23,1 David Austin. Penrose Tiles Talk Across Miles. Feature Column from the AMS. Дата обращения: 18 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ Burger, R. The Undecidability of the Domino Problem (англ.) // Memoirs of the American Mathematical Society. — 1966. — Vol. 66. — P. 1—72.
- ↑ R. Penrose (недоступная ссылка). Tilings Encyclopedia. Дата обращения: 13 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ 26,0 26,1 Socolar J. An Aperiodic Hexagonal Tile (неопр.). — . — arXiv:1003.4279.
- ↑ Socolar and Taylor’s aperiodic tile. Maxwell's Demon. Дата обращения: 18 августа 2013. Архивировано 2 сентября 2013 года.
- ↑ Weisstein, Eric W. Spherical Polyhedron (англ.) на сайте Wolfram MathWorld.
- ↑ Кокстер, Введение в геометрию, 1966, гл. 16, с. 415 — 440.
- ↑ 30,0 30,1 Мартин Гарднер. Математические головоломки и развлечения = Mathematical Puzzles and Diversions / Пер. Ю. А. Данилова, под ред. Я. А. Смородинского. — 2-е. — М.: Мир, 1999. — ISBN 5-03-003340-8.
- ↑ Weisstein, Eric W. Triangle Tiling (англ.) на сайте Wolfram MathWorld.
- ↑ Weisstein, Eric W. Quadrilateral Tiling (англ.) на сайте Wolfram MathWorld.
- ↑ Michaël Rao. Exhaustive search of convex pentagons which tile the plane Архивная копия от 2 августа 2017 на Wayback Machine
- ↑ Математик нашел все паркетные многоугольники
- ↑ Weisstein, Eric W. HexagonTiling (англ.) на сайте Wolfram MathWorld.
- ↑ Weisstein, Eric W. Tiling (англ.) на сайте Wolfram MathWorld.
Литература
- А. Н. Колмогоров. Паркеты из правильных многоугольников // Квант. — 1970. — № 3.
- Ю. А. Шашкин. Паркеты // МИФ. — 1998—99. — № 3.
- О. Михайлов. Одиннадцать правильных паркетов // Квант. — 1979. — № 2. Архивировано 22 мая 2013 года.
- Дэвид А. Кларнер. Математический цветник. Сборник статей и задач = The Mathematical Gardner / Пер. с англ. Ю. А. Данилова; под ред., с предисл. и прилож. И. М. Яглома. — М.: Мир, 1983. — С. 153—328. — 494 с.
- Г. С. М. Кокстер. Введение в геометрию = Introduction to geometry / Пер. с англ. А. Б. Катка и С. Б. Каток; под ред. Б. А. Розенфельда и И. М. Яглома. — М.: Наука, 1966. — 648 с.
- Grünbaum, Branko; Shephard, G. C. Tilings and Patterns (неопр.). — W. H. Freeman and Company[англ.], 1987. — ISBN 0-7167-1193-1.
Ссылки
- Хайдар Нурлигареев. Замощения. Элементы. Архивировано 16 августа 2013 года.
- Геометрические паркеты. Растрёпанный Блокнот. Архивировано 4 ноября 2011 года.
- Влад Алексеев. Математическое искусство М.К. Эшера. Невозможный мир. Архивировано 8 августа 2013 года.
- Wolfram Alpha учащимся Замощения
- Jaap Scherphuis. Tilings. Jaap's Puzzle Page. Дата обращения: 15 августа 2013. Архивировано 2 сентября 2013 года.
- Don Hatch. Hyperbolic Planar Tessellations. — Изображения усечённых гиперболических паркетов. Дата обращения: 20 августа 2013. Архивировано 2 сентября 2013 года.
- David E. Joyce. Hyperbolic Tessellations. — Java-апплет для отрисовки правильных и квазиправильных паркетов на гиперболической плоскости. Дата обращения: 23 августа 2013. Архивировано 2 сентября 2013 года.
- Vladimir Bulatov. Tilings of the hyperbolic space and their visualization. Joint MAA/AMS meeting, New Orleans (7 января 2011). Дата обращения: 20 августа 2013. Архивировано 2 сентября 2013 года.
- Demonolog. Гибридное замощение Применение векторной графики для изображения непериодических замощений.










![Усечённый шестиугольный паркет[англ.] 3.12.12](https://cdn.xn--h1ajim.xn--p1ai/images/thumb/4/47/Tiling_Semiregular_3-12-12_Truncated_Hexagonal.svg/160px-Tiling_Semiregular_3-12-12_Truncated_Hexagonal.svg.png)
![Ромбоусечённый тришестиугольный паркет[англ.] 4.6.12](https://cdn.xn--h1ajim.xn--p1ai/images/thumb/f/fe/Tiling_Semiregular_4-6-12_Great_Rhombitrihexagonal.svg/160px-Tiling_Semiregular_4-6-12_Great_Rhombitrihexagonal.svg.png)
![Изокурносый треугольный паркет[англ.] 3.3.3.4.4](https://cdn.xn--h1ajim.xn--p1ai/images/thumb/6/6e/Tiling_Semiregular_3-3-3-4-4_Elongated_Triangular.svg/160px-Tiling_Semiregular_3-3-3-4-4_Elongated_Triangular.svg.png)










