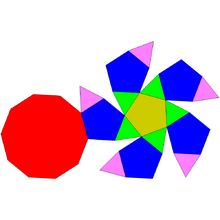
Пятискатная ротонда

Пятискатная ротонда
(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклая
Комбинаторика
Элементы	17 граней 35 рёбер 20 вершин Χ = 2
Грани	10 треугольников 6 пятиугольников 1 десятиугольник
Конфигурация вершины	2x5(3.5.3.5) 10(3.5.10)
Развёрткаразвернуть
Классификация
Обозначения	J6, М9
Группа симметрии	C5v

Пятиска́тная рото́нда — один из многогранников Джонсона (J₆, по Залгаллеру — М₉).

Составлена из 17 граней: 10 правильных треугольников, 6 правильных пятиугольников и 1 правильного десятиугольника. Десятиугольная грань окружена пятью пятиугольными и пятью треугольными; среди пятиугольных граней 5 окружены десятиугольной и четырьмя треугольными, 1 — пятью треугольными; среди треугольных граней 5 окружены десятиугольной и двумя пятиугольными, другие 5 — тремя пятиугольными.

Имеет 35 рёбер одинаковой длины. 5 рёбер располагаются между десятиугольной и пятиугольной гранями, 5 рёбер — между десятиугольной и треугольной, остальные 25 — между пятиугольной и треугольной.

У пятискатной ротонды 20 вершин. В 10 вершинах сходятся десятиугольная, пятиугольная и треугольная грани; в других 10 — две пятиугольных и две треугольных.

Пятискатные ротонды можно получить из икосододекаэдра, разрезав его на две равные части. Вершины каждого из двух полученных многогранников — 20 из 30 вершин икосододекаэдра, рёбра — 35 из 60 рёбер икосододекаэдра; отсюда ясно, что у пятискатных ротонд существуют описанная и полувписанная сферы, причём они совпадают с описанной и полувписанной сферами исходного икосододекаэдра. Центры описанных и полувписанных сфер совпадают с центрами десятиугольных граней ротонд.

Метрические характеристики

Если пятискатная ротонда имеет ребро длины [math]\displaystyle{ a }[/math], её площадь поверхности и объём выражаются как

[math]\displaystyle{ S = \frac{1}{2}\left(5\sqrt3+\left(5+3\sqrt5\right)\sqrt{5+2\sqrt5}\right)a^2 \approx 22{,}3472003a^2, }[/math]

[math]\displaystyle{ V = \frac{1}{12}\left(45+17\sqrt5\right)a^3 \approx 6{,}9177630a^3. }[/math]

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

[math]\displaystyle{ R = \frac{1}{2}\left(1+\sqrt5\right)a \approx 1{,}6180340a, }[/math]

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

[math]\displaystyle{ \rho = \frac{1}{2}\sqrt{5+2\sqrt5}\;a \approx 1{,}5388418a, }[/math]

высота ротонды (расстояние между десятиугольной и параллельной ей пятиугольной гранями) —

[math]\displaystyle{ H = \sqrt{1+\frac{2}{\sqrt5}}\;a \approx 1{,}3763819a. }[/math]

При одинаковой длине ребра высота пятискатной ротонды больше высоты пятискатного купола (J₅) в [math]\displaystyle{ \Phi^2 = \Phi+1 \approx 2{,}618 }[/math] раз, где [math]\displaystyle{ \Phi = \frac{1+\sqrt5}{2} }[/math] — отношение золотого сечения.

Ссылки

• Weisstein, Eric W. Пятискатная ротонда (англ.) на сайте Wolfram MathWorld.