Конформно-евклидова модель
Конформно-евклидова модель или модель Пуанкаре́ — модель пространства Лобачевского.
Существуют разновидности модели — в круге (стереографическая проекция) и на полуплоскости для планиметрии Лобачевского, а также в шаре и в полупространстве — для стереометрии Лобачевского, соответственно.
Конформно-евклидова модель примечательна тем, что в ней углы изображаются обычными углами, то есть эта модель конформна[1] в отличие от проективной модели, в которой определение углов производится гораздо сложнее.
История
Эта модель была предложена Эудженио Бельтрами, наряду с проективной моделью и моделью псевдосферы.[2] Метрика в конформно-евклидовой модели также в знаменитой лекции Римана «О гипотезах, лежащих в основании геометрии», но связь с геометрией Лобачевского обнаружена именно Бельтрами. Впоследствии Анри Пуанкаре обнаружил связи этой модели с задачами теории функций комплексного переменного, что дало одно из первых серьёзных приложений геометрии Лобачевского.
Модели в круге и в шаре

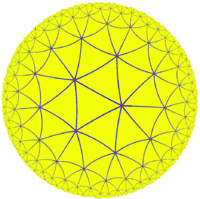
За плоскость Лобачевского принимается внутренность круга (изображено на иллюстрации) в евклидовом пространстве; граница данного круга (окружность) называется «абсолютом». Роль геодезических прямых выполняют содержащиеся в этом круге дуги окружностей [math]\displaystyle{ (a,\;b,\;b') }[/math], перпендикулярных абсолюту, и его диаметры; роль движений — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.
Метрикой [math]\displaystyle{ ds }[/math] плоскости Лобачевского в Конформно-евклидовой модели в единичном круге является:
- [math]\displaystyle{ ds^2=\frac{4}{(1-(x^2+y^2))^2}(dx^2+dy^2), }[/math]
где [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y }[/math] — оси абсцисс и ординат, соответственно[3].
Аналогично, для конформно-евклидовой модели в шаре роль абсолюта выполняет граничная сфера в трёхмерном евклидовом пространстве, а пространством Лобачевского является внутренность шара.
Расстояния
В комплексных координатах на единичном круге расстояния можно вычислить с помощью следующей формулы:
- [math]\displaystyle{ \mathop{\rm th}[\tfrac12\cdot d_h(z,w)]=\left|\frac{z-w}{1-z\cdot \bar w}\right|. }[/math]
Расстояние можно выразить через двойное отношение. Если на дуге [math]\displaystyle{ w_1 }[/math], [math]\displaystyle{ z_1 }[/math] точки расположены в следующем порядке: [math]\displaystyle{ w_1 }[/math], [math]\displaystyle{ w }[/math], [math]\displaystyle{ z }[/math], [math]\displaystyle{ z_1 }[/math] то расстояние между точками [math]\displaystyle{ w }[/math] и [math]\displaystyle{ z }[/math], в геометрии Лобачевского равняется
- [math]\displaystyle{ d_h(z,w)= \ln \left(\frac{z-w_1}{z-z_1}: \frac{w-w_1}{w-z_1}\right) }[/math].
Модели на полуплоскости и в полупространстве
В модели полуплоскости Пуанкаре за плоскость Лобачевского принимается верхняя полуплоскость. Прямая, ограничивающая полуплоскость (то есть ось абсцисс), называется «абсолютом». Роль прямых выполняют содержащиеся в этой полуплоскости полуокружности с центрами на абсолюте и начинающиеся на абсолюте перпендикулярные ему лучи (то есть вертикальные лучи). Роль движений — преобразования, получаемые композицией конечного числа инверсий с центром на абсолюте и осевых симметрий, оси которых перпендикулярны абсолюту.
Метрика [math]\displaystyle{ ds }[/math] плоскости Лобачевского в конформно-евклидовой модели в верхней полуплоскости имеет вид: [math]\displaystyle{ ds^2=\frac{1}{v^2}(du^2+dv^2) }[/math][3], где [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] — прямоугольные координаты, соответственно параллельно и перпендикулярно абсолюту.
Соответственно, в конформно-евклидовой модели в полупространстве роль абсолюта выполняет плоскость в трёхмерном евклидовом пространстве, а пространством Лобачевского является лежащее на этой плоскости полупространство.
См. также
- Теорема Пика — инвариантная форма леммы Шварца, использующая расстояния в конформно-евклидовой модели.
Примечания
- ↑ Попов А. Г. Псевдосферические поверхности и некоторые задачи математической физики. Дата обращения: 24 июля 2007. Архивировано 20 марта 2022 года.
- ↑ Eugenio Beltrami, Teoria fondamentale degli spazii di curvatura costante, Annali. di Mat., ser II, 2 (1868), 232—255.
перевод: Бельтрами Э. Основы теории пространств постоянной кривизны. // Об основаниях геометрии : Сборник. — М.: ГИТТЛ, 1956. — С. 342—365. - ↑ 3,0 3,1 Буяло С. В. Курс лекций «Асимптотическая геометрия метрических пространств» весна 2004.
Литература
- Черников Н. А. Преобразование Боголюбова и планиметрия Лобачевского. Раздел 4, сравнение двух моделей Пуанкаре. (недоступная ссылка с 18-05-2013 [4218 дней] — история)
- Самаров К., Уроев В. «Модель Пуанкаре». — Журнал «Квант». — 1984 год. — номер 6.