Описанная сфера
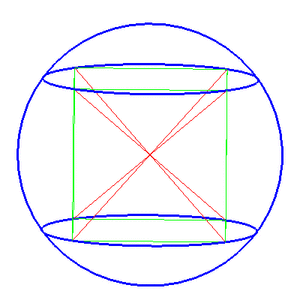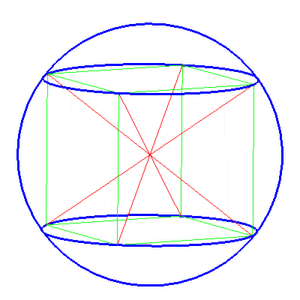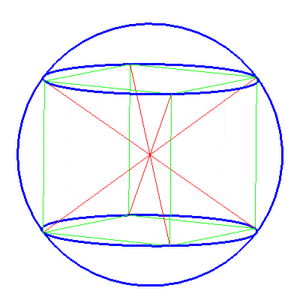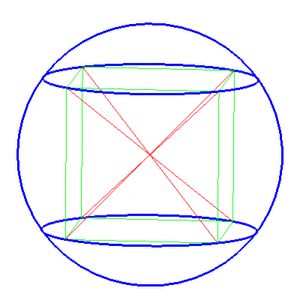
Описанная сфера — сфера, содержащая внутри себя многогранник, все вершины которого лежат на сфере.[1][2] В двумерном случае описанная сфера представляет собой описанную окружность.[3]
Существование
Если такая сфера существует, она не обязательно является наименьшей содержащей многогранник сферой. Например, тетраэдр, образованный вершиной куба и тремя её соседями, обладает той же описанной сферой, что и куб, но данный тетраэдр можно поместить в меньшую сферу, в которой три соседние вершины будут лежать на экваторе. Наименьшая сфера, содержащая данный многогранник, является описанной сферой для выпуклой оболочки подмножества вершин многогранника.[4]
Связанные понятия
Описанная сфера является трёхмерным аналогом описанной окружности. Все правильные многогранники обладают описанными сферами, но большинство неправильных многогранников не имеет описанных сфер, поскольку в общем случае не все вершины могут лежать на одной сфере. Описанная сфера (при её наличии) является примером ограничивающей сферы. Для любого многогранника можно определить наименьшую ограничивающую сферу.[4]
Среди других сфер, определяемых для некоторых многогранников, можно отметить полувписанную сферу, касающуюся всех рёбер многогранника, и вписанную сферу, касающуюся всех граней многогранника. Для правильных многогранников все три сферы существуют и являются концентрическими.[5]
Примечания
- ↑ James, R. C. (1992), The Mathematics Dictionary, Springer, с. 62, ISBN 9780412990410, <https://books.google.com/books?id=UyIfgBIwLMQC&pg=PA62> Архивная копия от 22 декабря 2021 на Wayback Machine.
- ↑ Popko, Edward S. (2012), Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere, CRC Press, с. 144, ISBN 9781466504295, <https://books.google.com/books?id=WLAFlr1_2S4C&pg=PA144> Архивная копия от 22 декабря 2021 на Wayback Machine.
- ↑ Smith, James T. (2011), Methods of Geometry, John Wiley & Sons, с. 419, ISBN 9781118031032, <https://books.google.com/books?id=B0khWEZmOlwC&pg=PA419> Архивная копия от 22 декабря 2021 на Wayback Machine.
- ↑ 4,0 4,1 Fischer, Kaspar; Gärtner, Bernd & Kutz, Martin (2003), Fast smallest-enclosing-ball computation in high dimensions, Algorithms - ESA 2003: 11th Annual European Symposium, Budapest, Hungary, September 16-19, 2003, Proceedings, vol. 2832, Lecture Notes in Computer Science, Springer, с. 630–641, DOI 10.1007/978-3-540-39658-1_57.
- ↑ Coxeter, H. S. M. (1973), 2.1 Regular polyhedra; 2.2 Reciprocation, Regular Polytopes (3rd ed.), Dover, с. 16–17, ISBN 0-486-61480-8.
Ссылки
- Weisstein, Eric W. Circumsphere (англ.) на сайте Wolfram MathWorld.