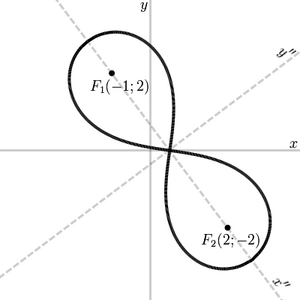
Лемниската Бернулли

Лемниската и её фокусы

Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Лемниската по форме напоминает арабскую цифру «восемь» или символ бесконечности. Точка, в которой лемниската пересекает саму себя, называется узловой, или двойной.

История

Название происходит от др.-греч. λημνίσκος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Данный вид лемнискаты назван в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.

Уравнение лемнискаты впервые опубликовано в статье Curvatura Laminae Elasticae Якоба Бернулли в журнале Acta eruditorum в 1694 году. Бернулли назвал эту кривую lemniscus; он не знал, что четырнадцатью годами ранее Джованни Кассини уже исследовал более общий случай. Квадратуру лемнискаты впервые выполнил Джюлио-Карло Фаньяно, опубликовав в 1718 году статью Metodo per misurare la lemniscata и положив тем самым начало изучению эллиптических интегралов, продолженное впоследствии Леонардом Эйлером. Некоторые свойства кривой были также исследованы Якобом Штейнером в 1835 году.

Уравнения

Рассмотрим простейший случай: если расстояние между фокусами равняется [math]\displaystyle{ 2c }[/math], расположены они на оси [math]\displaystyle{ OX }[/math], и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

• Параметрическое в прямоугольных координатах:

  [math]\displaystyle{ x = \frac{c\sqrt{2}\cos(t)}{1 + \sin^2(t)}; \qquad y = \frac{c\sqrt{2}\sin(t)\cos(t)}{1 + \sin^2(t)} }[/math]

• в прямоугольных координатах:

[math]\displaystyle{ \textstyle (x^2 + y^2)^2 = 2c^2 (x^2 - y^2) }[/math]

Выводразвернуть

Фокусы лемнискаты — [math]\displaystyle{ F_1(-c;0) }[/math] и [math]\displaystyle{ F_2(c;0) }[/math]. Возьмём произвольную точку [math]\displaystyle{ M(x;y) }[/math]. Произведение расстояний от фокусов до точки [math]\displaystyle{ M }[/math] есть

[math]\displaystyle{ \sqrt{(x+c)^2+y^2}\cdot\sqrt{(x-c)^2+y^2} }[/math],

и по определению оно равно [math]\displaystyle{ c^2 }[/math]:

[math]\displaystyle{ \sqrt{(x+c)^2+y^2}\cdot\sqrt{(x-c)^2+y^2}=c^2 }[/math]

Возводим в квадрат обе части равенства:

[math]\displaystyle{ \textstyle \Big((x+c)^2+y^2\Big)\cdot\Big( (x-c)^2+y^2\Big)=c^4 }[/math]

Раскрываем скобки в левой части:

[math]\displaystyle{ \textstyle (x^2-c^2)^2+y^4+2y^2(x^2+c^2)=c^4 }[/math]

Раскрываем скобки и свёртываем новый квадрат суммы:

[math]\displaystyle{ \textstyle (x^2+y^2)^2-2x^2c^2+2y^2c^2=0 }[/math]

Выносим общий множитель и переносим:

[math]\displaystyle{ \textstyle (x^2+y^2)^2=2c^2(x^2-y^2) }[/math]

Далее можно сделать замену [math]\displaystyle{ a^2=2c^2 }[/math], хотя это не обязательно:

[math]\displaystyle{ \textstyle (x^2+y^2)^2=a^2(x^2-y^2) }[/math]

В данном случае [math]\displaystyle{ a }[/math] — радиус окружности, описывающей лемнискату.

Проведя несложные преобразования, можно получить явное уравнение:

[math]\displaystyle{ \textstyle y=\pm\sqrt{\sqrt{c^4+4x^2 c^2}-x^2-c^2} }[/math]

Выводразвернуть

[math]\displaystyle{ \textstyle (x^2+y^2)^2=2c^2(x^2-y^2) }[/math]

Возводим в квадрат и раскрываем скобки:

[math]\displaystyle{ \textstyle x^4+2x^{2}y^2+y^4=2c^{2}x^2-2c^{2}y^2 }[/math]

Приводим к виду

[math]\displaystyle{ \textstyle y^4+2y^{2}(x^2+c^2)+x^4-2c^{2}x^2=0 }[/math]

Это квадратное уравнение относительно [math]\displaystyle{ y^2 }[/math]. Решив его, получим

[math]\displaystyle{ \textstyle y^2=-(x^2+c^2)\pm\sqrt{c^4+4x^{2}c^2} }[/math]

Взяв корень и отбросив вариант с отрицательным вторым слагаемым, получим:

[math]\displaystyle{ \textstyle y=\pm\sqrt{\sqrt{c^4+4x^2 c^2}-x^2-c^2} }[/math]

где положительный вариант определяет верхнюю половину лемнискаты, отрицательный — нижнюю.

• в полярных координатах:

[math]\displaystyle{ \textstyle \rho^2 = 2c^2 \cos 2\varphi. }[/math]

Выводразвернуть

[math]\displaystyle{ \textstyle (x^2+y^2)^2=2c^2(x^2-y^2) }[/math]

Используя формулы перехода к полярной системе координат [math]\displaystyle{ x=\rho\cos\varphi,\,y=\rho\sin\varphi, }[/math] получим:

[math]\displaystyle{ \Big(\rho^2\cos^{2}\varphi+\rho^2\sin^{2}\varphi\Big)^2=2c^2\Big(\rho^2\cos^2\varphi-\rho^2\sin^2\varphi\Big) }[/math]

Выносим общие множители и используем тригонометрическое тождество [math]\displaystyle{ \sin^2 \alpha + \cos^2 \alpha = 1 }[/math]:

[math]\displaystyle{ \textstyle\rho^4=2c^2\rho^2(\cos^2\varphi-\sin^2\varphi) }[/math]

Делим на [math]\displaystyle{ \rho^2 }[/math], предполагая, что [math]\displaystyle{ \rho\neq 0 }[/math] и используем ещё одно тождество: [math]\displaystyle{ \cos^2 \alpha - \sin^2 \alpha = cos 2\alpha }[/math]:

[math]\displaystyle{ \textstyle\rho^2=2c^2\cos 2\varphi }[/math]

Как и в случае прямоугольной системы можно заменить [math]\displaystyle{ a^2=2c^2 }[/math]:

[math]\displaystyle{ \textstyle\rho^2=a^2\cos 2\varphi }[/math]

Плотность точек кривой при равномерном изменении параметра

• Параметрическое уравнение в прямоугольной системе:

[math]\displaystyle{ \begin{cases}x=c \sqrt{2}\frac{p+p^3}{1+p^4} \\ y=c\sqrt{2} \frac{p-p^3}{1+p^4}\end{cases} }[/math], где [math]\displaystyle{ p^2=\operatorname{tg}\Big(\frac{\pi}{4}-\varphi\Big) }[/math]

Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от [math]\displaystyle{ -\infty }[/math] до [math]\displaystyle{ +\infty }[/math]. При этом, когда параметр стремится к [math]\displaystyle{ -\infty }[/math], точка кривой стремится к [math]\displaystyle{ (0;0) }[/math] из второй координатной четверти, а когда параметр стремится к [math]\displaystyle{ +\infty }[/math], то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.

Вывод уравненияразвернуть

Уравнение лемнискаты в полярной системе

[math]\displaystyle{ \textstyle\rho^2=2c^2\cos 2\varphi }[/math]

подставим в формулы перехода к полярной системе координат [math]\displaystyle{ x=\rho\cos\varphi,\,y=\rho\sin\varphi, }[/math] возведённые в квадрат:

[math]\displaystyle{ \textstyle\begin{cases}x^2=2c^2\cos2\varphi\cos^2\varphi\\y^2=2c^2\cos2\varphi\sin^2\varphi\end{cases} }[/math]

Используем тригонометрические формулы [math]\displaystyle{ \textstyle \cos 2\alpha=\dfrac{1-\operatorname{tg}^2\alpha}{1+\operatorname{tg}^2\alpha}, \textstyle\cos^2\alpha=\dfrac{1}{1+\operatorname{tg}^2\alpha} }[/math] и [math]\displaystyle{ \textstyle\sin^2\alpha=\dfrac{\operatorname{tg}^2\alpha}{1+\operatorname{tg}^2\alpha} }[/math]:

[math]\displaystyle{ \textstyle\begin{cases}x^2=2c^2\dfrac{1-\operatorname{tg}^2\varphi}{\left (1+\operatorname{tg}^2\varphi\right )^2}\\y^2=2c^2\dfrac{\operatorname{tg}^2\varphi\left (1-\operatorname{tg}^2\varphi\right )}{\left (1+\operatorname{tg}^2\varphi\right )^2}\end{cases} }[/math]

Используем ещё одно легко выводимое тригонометрическое соотношение [math]\displaystyle{ \operatorname{tg}\alpha=\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\alpha\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\alpha\right)} }[/math]:

[math]\displaystyle{ \textstyle\begin{cases}x^2=2c^2\dfrac{1-\left (\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}\right )^2}{\left (1+\left (\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}\right )^2\right )^2}\\y^2=2c^2\dfrac{\left (\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}\right )^2\left (1-\left (\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}\right )^2\right )}{\left (1+\left (\dfrac{1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}{1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}\right )^2\right )^2}\end{cases} }[/math]

Выполнив необходимые преобразования, получаем:

[math]\displaystyle{ \textstyle\begin{cases}x^2=2c^2\dfrac{\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\left(1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\right)^2}{\left(1+\operatorname{tg}^2\left(\frac{\pi}{4}-\varphi\right)\right)^2}\\y^2=2c^2\dfrac{\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\left(1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\right)^2}{\left(1+\operatorname{tg}^2\left(\frac{\pi}{4}-\varphi\right)\right)^2}\end{cases} }[/math]

Извлекаем корень из обеих частей обоих равенств:

[math]\displaystyle{ \textstyle\begin{cases}x=c\sqrt{2}\dfrac{\left(1+\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\right)\sqrt{\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}}{1+\operatorname{tg}^2\left(\frac{\pi}{4}-\varphi\right)}\\y=c\sqrt{2}\dfrac{\left(1-\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)\right)\sqrt{\operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)}}{1+\operatorname{tg}^2\left(\frac{\pi}{4}-\varphi\right)}\end{cases} }[/math]

Если произвести замену [math]\displaystyle{ \textstyle \operatorname{tg}\left(\frac{\pi}{4}-\varphi\right)=p^2 }[/math], то получаем искомые параметрические уравнения:

[math]\displaystyle{ \textstyle\begin{cases}x=c\sqrt{2}\frac{p+p^3}{1+p^4}\\y=c\sqrt{2}\frac{p-p^3}{1+p^4}\end{cases} }[/math]

• Чтобы задать лемнискату по двум произвольным точкам, можно не выводить уравнение заново, а определить преобразование координат, при котором старый (данный) фокусный отрезок переходит в новый, и воздействовать на представленные уравнения этим преобразованием.

Примерразвернуть

Пусть, например, [math]\displaystyle{ F_1(-1;2),\,F_2(2;-2) }[/math] — фокусы.

Существует прямоугольная система координат (на рисунке — [math]\displaystyle{ \textstyle x''Oy'' }[/math]), в которой уравнение лемнискаты имеет вид

[math]\displaystyle{ \textstyle \Big((x'')^2 + (y'')^2\Big)^2 - 2c^2 \Big((x'')^2 - (y'')^2\Big) = 0 }[/math]

Необходимо определить преобразование системы координат, переводящее [math]\displaystyle{ \textstyle xOy }[/math] в [math]\displaystyle{ \textstyle x''Oy'' }[/math]. Это преобразование осуществляется в два этапа: параллельный перенос и поворот.

Середина отрезка [math]\displaystyle{ F_1F_2 }[/math] — [math]\displaystyle{ \textstyle F\left (\frac{1}{2};0\right ) }[/math], значит перенос только на [math]\displaystyle{ \textstyle+\frac{1}{2} }[/math] по оси [math]\displaystyle{ OX }[/math]:

[math]\displaystyle{ \begin{cases}x'=x-x_0 \\ y'=y-y_0\end{cases}=\begin{cases}x'=x-\frac{1}{2} \\ y'=y\end{cases} }[/math]

После переноса системы координат её надо повернуть на некоторый угол. Для определения угла сначала найдём расстояние между фокусами:

[math]\displaystyle{ 2c=|F_1 F_2|=\sqrt{(2+1)^2+(-2-2)^2}=5 }[/math]

значит [math]\displaystyle{ c=\frac{5}{2},\,2c^2=\frac{25}{2} }[/math].

Теперь из геометрических соображений находим синус и косинус угла наклона [math]\displaystyle{ F_1 F_2 }[/math] к [math]\displaystyle{ OX }[/math]:

[math]\displaystyle{ \sin\alpha=\frac{-2-2}{5}=-\frac{4}{5},\,\,(\alpha\approx -53^\circ) }[/math]

[math]\displaystyle{ \cos\alpha=\frac{2-(-1)}{5}=\frac{3}{5} }[/math]

Формулы преобразования:

[math]\displaystyle{ \begin{cases}x''=x'\cos\alpha+y'\sin\alpha \\ y''=-x'\sin\alpha+y'\cos\alpha\end{cases}=\begin{cases}x''=\frac{3}{5}x'-\frac{4}{5}y' \\ y''=\frac{4}{5}x'+\frac{3}{5}y'\end{cases} }[/math]

Совместив оба преобразования, получим конечные формулы перехода:

[math]\displaystyle{ \begin{cases}x''=\frac{3}{5}(x-\frac{1}{2})-\frac{4}{5}y \\ y''=\frac{4}{5}(x-\frac{1}{2})+\frac{3}{5}y\end{cases} }[/math]

Для того, чтобы получить уравнение в стандартной системе координат, подставим эти соотношения в исходное уравнение кривой:

[math]\displaystyle{ \textstyle \bigg(\Big(\frac{3}{5}(x-\frac{1}{2})-\frac{4}{5}y\Big)^2 + \Big(\frac{4}{5}(x-\frac{1}{2})+\frac{3}{5}y\Big)^2\bigg)^2 - 2c^2 \bigg(\Big(\frac{3}{5}(x-\frac{1}{2})-\frac{4}{5}y\Big)^2 - \Big(\frac{4}{5}(x-\frac{1}{2})+\frac{3}{5}y\Big)^2\bigg) = 0 }[/math]

После преобразований:

[math]\displaystyle{ x^4+y^4+24xy-2xy^2+2x^2y^2-2x^3+5x^2-4x-3y^2-12y+\frac{15}{16}=0 }[/math]

Это уравнение задаёт лемнискату с фокусами [math]\displaystyle{ F_1(-1;2),\,F_2(2;-2) }[/math] в стандартной прямоугольной системе координат.

Свойства

Некоторые свойства лемнискаты:
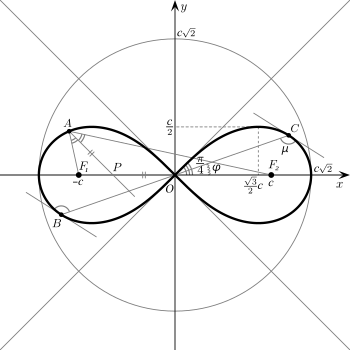
1. Симметрия относительно узловой точки;
2. Касательные в узловой точке имеют углы [math]\displaystyle{ \textstyle\pm\frac{\pi}{4} }[/math];
3. Для любой точки [math]\displaystyle{ A }[/math] лемнискаты выполняется: [math]\displaystyle{ AP=PO }[/math], где [math]\displaystyle{ AP }[/math] — биссектриса [math]\displaystyle{ \angle F_1AF_2 }[/math];
4. [math]\displaystyle{ \textstyle\mu=2\varphi+\frac{\pi}{2} }[/math] для любой точки кривой;

Лемниската Бернулли является частным случаем овала Кассини при [math]\displaystyle{ a=c }[/math], синусоидальной спирали с индексом [math]\displaystyle{ n=2 }[/math] и лемнискаты Бута при [math]\displaystyle{ c=0 }[/math], поэтому она наследует некоторые свойства этих кривых.

Свойства, верные для произвольных овалов Кассини

• Лемниската — кривая четвёртого порядка.
• Она симметрична относительно двойной точки — середины отрезка между фокусами.
• Кривая имеет 2 максимума и 2 минимума. Их координаты:

  [math]\displaystyle{ \begin{cases}x=\pm\frac{\sqrt{3}}{2}c\\ y=\pm\frac{c}{2}\end{cases} }[/math]

• Расстояние от максимума до минимума, находящихся по одну сторону от серединного перпендикуляра отрезка между фокусами равно расстоянию от максимума (или от минимума) до двойной точки.
• Лемнискату описывает окружность радиуса [math]\displaystyle{ a=c\sqrt{2} }[/math], поэтому иногда в уравнениях производят эту замену.

Свойства, верные для произвольных синусоидальных спиралей

• Касательные в двойной точке составляют с отрезком [math]\displaystyle{ F_1F_2 }[/math] углы [math]\displaystyle{ \textstyle\pm\frac{\pi}{4} }[/math].
• Угол [math]\displaystyle{ \mu }[/math], составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен [math]\displaystyle{ \textstyle 2\varphi+\frac{\pi}{2} }[/math].
• Касательные в точках пересечения кривой и хорды, проходящей через двойную точку, параллельны друг другу.
• Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.
• Радиус кривизны лемнискаты есть [math]\displaystyle{ \textstyle R=\frac{2c^2}{3\rho} }[/math]

развернутьВывод

Есть частный случай формулы радиуса кривизны синусоидальной спирали: [math]\displaystyle{ R=\frac{\rho}{(m+1)\cos m\varphi} }[/math] при [math]\displaystyle{ m=2, }[/math] однако, легко вывести и по определению. Уравнение лемнискаты в полярной системе: [math]\displaystyle{ \rho^2=2c^2\cos{2\varphi} }[/math] Формулы перехода к полярной системе координат: [math]\displaystyle{ \begin{cases}x=\rho\cos{\varphi} \\ y=\rho\sin{\varphi}\end{cases} }[/math] Выражаем [math]\displaystyle{ \textstyle\rho }[/math]: [math]\displaystyle{ \begin{cases}\rho=\frac{x}{\cos{\varphi}} \\ \rho=\frac{y}{\sin{\varphi}}\end{cases} }[/math] Подставляем в уравнение лемнискаты и выражаем [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y }[/math]: [math]\displaystyle{ \begin{cases}\frac{x^2}{cos^2{\varphi}}=2c^2\cos{2\varphi} \\ \frac{y^2}{sin^2{\varphi}}=2c^2\cos{2\varphi}\end{cases}= \begin{cases}x=c\sqrt{2}\cos{\varphi}\sqrt{\cos{2\varphi}} \\ y=c\sqrt{2}\sin{\varphi}\sqrt{\cos{2\varphi}}\end{cases} }[/math] —- это параметрическое уравнение относительно [math]\displaystyle{ \varphi }[/math]. Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно [math]\displaystyle{ \textstyle p }[/math], указанное выше в разделе Уравнения. Формула радиуса кривизны кривой, заданной параметрически: [math]\displaystyle{ R=\frac{\Big((x')^2+(y')^2\Big)^{3/2}}{|x'y''-x''y'|} }[/math] Находим производные по [math]\displaystyle{ \varphi }[/math]: [math]\displaystyle{ x'=c\sqrt{2}\left ( -\sin{\varphi}\sqrt{\cos{2\varphi}}-\cos{\varphi}\frac{\sin{2\varphi}}{\sqrt{\cos{2\varphi}}}\right )=-c\sqrt{2}\frac{\sin{3\varphi}}{\sqrt{\cos{2\varphi}}} }[/math] [math]\displaystyle{ x''=-c\sqrt{2}\frac{3\cos{3\varphi}\sqrt{\cos{2\varphi}}+\frac{\sin{2\varphi}}{\sqrt{\cos{2\varphi}}}\sin{3\varphi}}{\cos{2\varphi}}=\ldots=-c\sqrt{2}\frac{2\cos{\varphi}+\cos{5\varphi}}{(\cos{2\varphi})^{3/2}} }[/math] [math]\displaystyle{ y'=c\sqrt{2}\left ( -\cos{\varphi}\sqrt{\cos{2\varphi}}-\sin{\varphi}\frac{\sin{2\varphi}}{\sqrt{\cos{2\varphi}}}\right )=c\sqrt{2}\frac{\cos{3\varphi}}{\sqrt{\cos{2\varphi}}} }[/math] [math]\displaystyle{ y''=c\sqrt{2}\frac{-3\sin{3\varphi}\sqrt{\cos{2\varphi}}+\frac{\sin{2\varphi}}{\sqrt{\cos{2\varphi}}}\cos{3\varphi}}{\cos{2\varphi}}=\ldots=-c\sqrt{2}\frac{2\sin{\varphi}+\sin{5\varphi}}{(\cos{2\varphi})^{3/2}} }[/math] Подставляем в формулу радиуса: [math]\displaystyle{ R=\ldots=\frac{\left (\frac{2c^2}{cos{2\varphi}}\right )^{3/2}}{\frac{6c^2}{\cos{2\varphi}}}=\frac{c\sqrt{2}}{3\sqrt{\cos{2\varphi}}} }[/math] Возвращаемся к уравнению лемнискаты: [math]\displaystyle{ \rho^2=2c^2\cos{2\varphi}\,\,\Rightarrow\,\,\sqrt{\cos{2\varphi}}=\frac{\rho}{c\sqrt{2}} }[/math] Подставляем это выражение в полученную формулу радиуса и получаем: [math]\displaystyle{ R=\frac{2c^2}{3\rho} }[/math]

• Натуральное уравнение кривой имеет вид

  [math]\displaystyle{ S=3\int\frac{\mathrm{d}R}{\sqrt{\left(\frac{3}{c}R\right)^4-1}} }[/math]

• Подерой лемнискаты является синусоидальная спираль

  [math]\displaystyle{ \textstyle \rho^{\frac{2}{3}}=(c\sqrt{2})^{\frac{2}{3}}\cos\frac{2}{3}\varphi. }[/math]

• Лемниската сама является подерой равносторонней гиперболы.

Собственные свойства

Таутохронность лемнискаты

• Кривая является геометрическим местом точек, симметричных центру равносторонней гиперболы относительно её касательных.
• Отрезок биссектрисы угла между фокальными радиусами-векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.
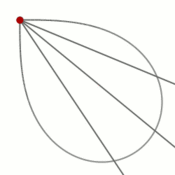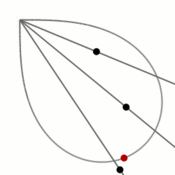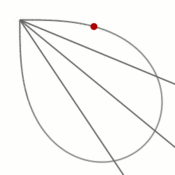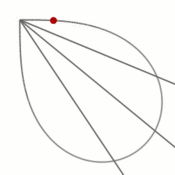
• Материальная точка, движущаяся по лемнискате под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду (см. рисунок). Предполагается, что ось лемнискаты составляет угол [math]\displaystyle{ 45^\circ }[/math] с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.
• Площадь полярного сектора [math]\displaystyle{ \varphi\in[0,\alpha] }[/math], при [math]\displaystyle{ \textstyle 0\leqslant\alpha\leqslant\frac{\pi}{4} }[/math]:

  [math]\displaystyle{ \textstyle S(\alpha)=\frac{c^2}{2}\sin2\alpha }[/math]

  • В частности, площадь каждой петли [math]\displaystyle{ \textstyle 2S\left (\frac{\pi}{4}\right )=c^2 }[/math], то есть площадь, ограниченная кривой, равна площади квадрата с диагональю [math]\displaystyle{ c\sqrt{2} }[/math].
• Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.
• Длина дуги лемнискаты между точками [math]\displaystyle{ \varphi_1=0 }[/math] и [math]\displaystyle{ \varphi_2=\varphi }[/math] выражается эллиптическим интегралом I рода:

  [math]\displaystyle{ \textstyle L(\varphi)=c\int\limits_0^\varphi\frac{\mathrm{d}\varphi}{\sqrt{1-2\sin^2\varphi}}=\frac{c}{\sqrt{2}}\int\limits_0^\theta\frac{\mathrm{d}\theta}{\sqrt{1-\frac{1}{2}\sin^2\theta}}=\frac{c}{\sqrt{2}}F\left(\theta,\frac{1}{\sqrt{2}}\right), }[/math] где [math]\displaystyle{ 2\sin^2\varphi=\sin^2\theta. }[/math]

  • В частности, длина всей лемнискаты

    [math]\displaystyle{ \textstyle 4L\left(\frac{\pi}{4}\right)=2c\sqrt{2}\,K\left(\frac{1}{\sqrt{2}}\right)\approx 5{,}244 a \approx 7{,}416 c. }[/math]

Построения

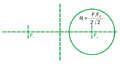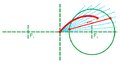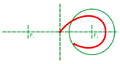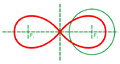
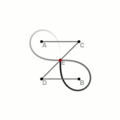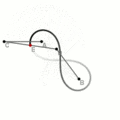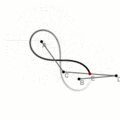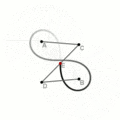
При помощи секущих (способ Маклорена)

Строится окружность радиуса [math]\displaystyle{ \textstyle\frac{c}{\sqrt{2}} }[/math] с центром в одном из фокусов. Из середины [math]\displaystyle{ O }[/math] фокусного отрезка строится произвольная секущая [math]\displaystyle{ OPS }[/math] ([math]\displaystyle{ P }[/math] и [math]\displaystyle{ S }[/math] — точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки [math]\displaystyle{ OM_1 }[/math] и [math]\displaystyle{ OM_2 }[/math], равные хорде [math]\displaystyle{ PS }[/math]. Точки [math]\displaystyle{ M_1 }[/math], [math]\displaystyle{ M_2 }[/math] лежат на разных петлях лемнискаты.

Шарнирные методы

Вариант первый

На плоскости выбираются две точки — [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] — будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба — [math]\displaystyle{ C }[/math] и [math]\displaystyle{ D }[/math]). При этом необходимо соблюсти пропорции отрезков: [math]\displaystyle{ \textstyle AC=BD=\frac{AB}{\sqrt{2}},\;CD=AB }[/math]. Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.

Вариант второй

В этом варианте лемниската строится по фокусу и двойной точке — [math]\displaystyle{ A }[/math] и [math]\displaystyle{ O }[/math] соответственно. Собирается почти такая же шарнирная конструкция как и в предыдущем варианте, но прикреплённый к двойной точке отрезок [math]\displaystyle{ OC }[/math] соединяется не с концом центрального [math]\displaystyle{ BD }[/math], а с его серединой. Пропорции также другие: [math]\displaystyle{ \textstyle BC=CD=OC=\frac{AO}{\sqrt{2}},\;AB=AO }[/math].

• 
  Построение лемнискаты при помощи секущих
• 
  Шарнирный метод
• 
  Механизм Ватта (анимация)
• 
  Другой вариант шарнирного метода

При помощи сплайна NURBS

Пример построения лемнискаты Бернулли с помощью сплайна NURBS.
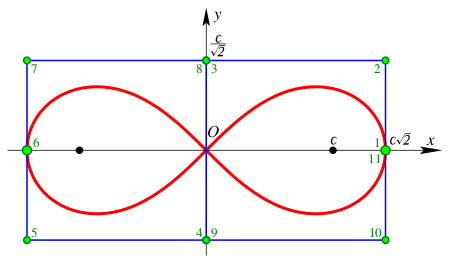
Синяя линия — контрольная ломаная сплайна. Зелёные кружки — контрольные точки сплайна. Размер кружков пропорционален весу контрольной точки. Зелёные числа рядом с контрольными точками — порядковые номера точек в контрольной ломаной.

Лемнискату Бернулли можно построить посредством сплайнов NURBS разными способами. Один из возможных способов представлен на рисунке. Параметры контрольных точек сплайна приведены в таблице:

№	[math]\displaystyle{ \frac{x\sqrt{2}}{c} }[/math]	[math]\displaystyle{ \frac{y\sqrt{2}}{c} }[/math]	[math]\displaystyle{ weight }[/math]
1	2	0	2
2	2	1	1
3	0	1	1
4	0	−1	1
5	−2	−1	1
6	−2	0	2
7	−2	1	1
8	0	1	1
9	0	−1	1
10	2	−1	1
11	2	0	2

Узловой вектор {−1, −1, −1, −1, −1, 0, 1, 1, 1, 1, 2, 3, 3, 3, 3, 3}. Такое представление NURBS кривой полностью совпадает с рациональным параметрическим преставлением в прямоугольной системе координат в диапазоне изменения параметра p в интервале: [math]\displaystyle{ -1 \le p \le 1 }[/math].

Обобщения

• Лемниската — общий случай с несколькими фокусами
• Овал Кассини — обобщение на произведение расстояний до фокусов
• Синусоидальная спираль — обобщение по виду параметрического уравнения (лемниската Бернулли получается при [math]\displaystyle{ n=2 }[/math])

См. также

• Лемниската Бута
• Лемниската Жероно
• Плоская кривая
• Алгебраическая кривая
• Бесконечность
• Аттрактор Лоренца

Литература

• Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1982.
• Маркушевич А. И. Замечательные кривые. — Популярные лекции по математике. — М.: Гостехиздат, 1952. — С. 23—25. Архивная копия от 14 сентября 2008 на Wayback Machine
• Савелов А. А. Плоские кривые / Под. ред. А. П. Нордена. — М.: ФИЗМАТГИЗ, 1960. — С. 155—162.
• Lockwood E. H. A book of curves. — Cambridge: Cambridge university press, 1961. — P. 110—117.

Ссылки

• Статья на сайте Wolfram MathWorld (англ.). Дата обращения: 15 июня 2010.
• Статья в Encyclopédie des Formes Mathématiques Remarquables (фр.). Дата обращения: 15 июня 2010. Архивировано 22 августа 2011 года.
• Фаньяно и длина дуги лемнискаты (итал.). Дата обращения: 15 июня 2010. Архивировано 22 августа 2011 года.