Полукубическая парабола
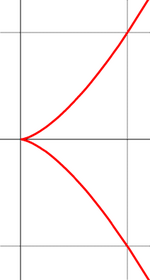
Полукубическая парабола, или парабола Нейла, — плоская алгебраическая кривая, описываемая уравнением y2=ax3 в некоторой прямоугольной системе координат. Названа по имени Нейла, который в 1657 году вычислил длину её дуги.
Уравнения
- Алгебраическое уравнение: y2=ax3 (a≠0).
- Параметрическое уравнение: x=t2, y=at3 (a≠0).
Свойства
Полукубическая парабола является каустикой кривой Чирнгаузена. Более того, любая каустика вида «ласточкин хвост» вблизи вершины хорошо приближается полукубической параболой, что делает эту кривую эталонной в теории катастроф.
Радиус кривизны полукубической параболы в начале координат равен нулю.
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |