Лемниската Бута
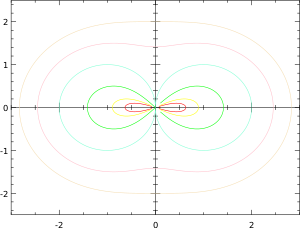
Лемниската Бута — плоская алгебраическая кривая четвёртого порядка, частный случай кривой Персея. Названа в честь Джеймса Бута.
Уравнение в прямоугольных декартовых координатах:
- [math]\displaystyle{ (x^2 + y ^2)^2 - (2m^2 + c)x^2 + (2m^2 - c)y^2 = 0. }[/math]
Виды
Форма кривой зависит от соотношения между параметрами [math]\displaystyle{ m }[/math] и [math]\displaystyle{ c }[/math]. Если [math]\displaystyle{ c \gt 2m^2 }[/math], то уравнение лемнискаты принимает вид
- [math]\displaystyle{ (x^2 + y ^2)^2 = a^2x^2 + b^2y^2 }[/math], где [math]\displaystyle{ a^2 = 2m^2 + c }[/math] и [math]\displaystyle{ b^2 = c - 2m^2. }[/math]
В этом случае лемниската Бута является подерой эллипса относительно его центра и называется эллиптической. Её уравнение в полярных координатах имеет вид
- [math]\displaystyle{ \rho^2 = a^2\cos^2 \phi + b^2\sin^2\phi. }[/math]
Если [math]\displaystyle{ c \lt 2m^2 }[/math], то уравнение лемнискаты принимает вид
- [math]\displaystyle{ (x^2 + y ^2)^2 = a^2x^2 - b^2y^2 }[/math], где [math]\displaystyle{ a^2 = 2m^2 + c }[/math] и [math]\displaystyle{ b^2 = 2m^2 - c. }[/math]
В этом случае лемниската Бута является подерой гиперболы относительно её центра и называется гиперболической. Её уравнение в полярных координатах имеет вид
- [math]\displaystyle{ \rho^2 = a^2\cos^2 \phi - b^2\sin^2\phi. }[/math]
Частные случаи
- При [math]\displaystyle{ c = 2m^2 }[/math] лемниската Бута вырождается в две окружности [math]\displaystyle{ x^2 + y^2 \pm 2mx = 0. }[/math]
- При [math]\displaystyle{ c = 0 }[/math] лемниската Бута вырождается в лемнискату Бернулли.
Свойства
- Лемниската Бута — ортогональная проекция на плоскость xOy линии пересечения поверхности параболоида [math]\displaystyle{ x^2 + y^2 = cz }[/math] с поверхностью конуса [math]\displaystyle{ a^2x^2 + b^2y^2 = c^2z^2. }[/math]
- Лемнискату Бута можно получить инверсией кривой второго порядка [math]\displaystyle{ a^2x^2 \pm b^2y^2 = k^4 }[/math] с центром в начале координат.
Площадь
С помощью полярного уравнения лемнискаты можно определить площадь, которую она ограничивает. Для эллиптической лемнискаты:
- [math]\displaystyle{ 2\int\limits_0^\frac{\pi}{2} (a^2\cos^2\phi + b^2\sin^2\phi) d\phi = \frac{\pi}{2}(a^2+b^2). }[/math]
Для гиперболической лемнискаты:
- [math]\displaystyle{ \int\limits_0^{\operatorname{arctg}\frac{a}{b}} (a^2\cos^2\phi - b^2\sin^2\phi) d\phi = \frac{a^2 - b^2}{2}\operatorname{arctg}\frac{a}{b} + \frac{ab}{2}. }[/math]
См. также
Литература
- А. А. Савелов. Кривые Персея // Плоские кривые: систематика, свойства, применение / под ред. А. П. Нордена. — М.: Государственное издательство физико-математической литературы, 1960. — С. 144—146. — 294 с.
- Математическая энциклопедия / под. ред. И. М. Виноградова. — «Советская энциклопедия», 1977. — Т. 1. — С. 566.
- Weisstein, Eric W. Hippopede (англ.) на сайте Wolfram MathWorld.
- Courbe de Booth (фр.)