Локсодрома

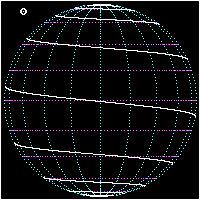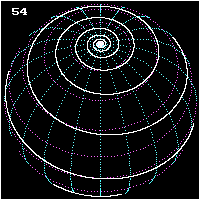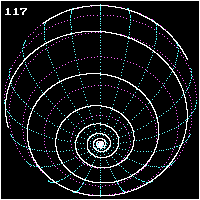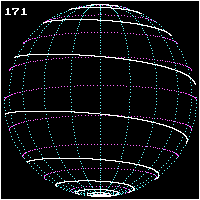
Локсодрома от полюса до полюса

Локсодрома, или локсодромия (от др.-греч. «λοξός» — «косой», «наклонный» и «δρόμος» — «путь») — кривая на поверхности вращения, пересекающая все меридианы под постоянным углом, называемым локсодромическим путевым углом.

История

Введена в рассмотрение португальским математиком Нониусом в 1529 году.

В труде «Tiphys batavus» (1624) нидерландский математик Виллеброрд Снелл пересекающую все меридианы под постоянным углом кривую назвал «локсодромой», исследовал её. Работа состояла из двух частей — теоретической и практических упражнений с рекомендациями.

В геодезии и картографии

На поверхности Земли локсодромами являются все параллели (путевой угол может быть равен 90°, 270° и т. д.) и все меридианы (путевой угол 0°, 180° и т. д.). Локсодромы под остальными углами являются спиралями, совершающими неограниченное число витков, приближаясь к полюсам. Тем не менее, если путешественник будет двигаться по любой локсодроме (кроме параллелей) с постоянной скоростью не останавливаясь, то он обязательно придёт к одному из полюсов за конечное время. Картографическая проекция, в которой все локсодромы изображены прямыми, называется проекцией Меркатора.

В навигации

Если передвигаться с фиксированным путевым углом по Земле, которую условно принять за сферу или геоид, то траектория движения объекта и будет локсодромией. Локсодрома не является кратчайшим путём между двумя пунктами (исключение — меридианы и экватор). Тем не менее, в старину суда и путешественники нередко двигались по локсодромам, так как идти под постоянным углом к Полярной звезде проще и удобнее. С изобретением компаса мореплаватели перешли на движение по «магнитным локсодромам», то есть по линиям с постоянным углом к магнитному северу, что дало возможность продолжать движение и в облачную погоду. Но как только были выяснены магнитные склонения во всех местах Земли, люди вновь перешли на обычные локсодромы. Даже в XX веке локсодромия использовалась при расчёте требуемого курса при прокладке маршрута самолётов и морских судов. Со временем, когда появились приборы с достаточной вычислительной мощностью для вычисления текущего требуемого путевого угла, начали активно применять ортодромию (кратчайший путь), особенно для дальних маршрутов самолётов.

Построение локсодромы сферы

Отрезок локсодромы, от экватора до полюса

Для того чтобы на полётных картах проложить локсодромический путь, необходимо соединить конечные точки маршрута прямой линией и измерить путевой угол у среднего меридиана. Точнее, локсодромический путевой угол рассчитывается как средний угол, снятый у начальной и конечной точек маршрута. После этого полученный путевой угол строят последовательно у всех меридианов на карте, начиная от пункта вылета. Полученная при построении ломаная линия практически близко подходит к локсодромии. Более точно локсодромический путевой угол [math]\displaystyle{ \alpha }[/math] может быть вычислен по формуле:

[math]\displaystyle{ \mathrm{tg} \alpha = \frac{\lambda_2 - \lambda_1}{\varphi_2 - \varphi_1} \cos \varphi_m }[/math],

• где [math]\displaystyle{ \alpha }[/math] — искомый путевой угол;
• [math]\displaystyle{ \varphi_1 }[/math] и [math]\displaystyle{ \varphi_2 }[/math] — широты пунктов вылета и прибытия;
• [math]\displaystyle{ \lambda_1 }[/math] и [math]\displaystyle{ \lambda_2 }[/math] — долготы этих пунктов;
• [math]\displaystyle{ \varphi_m }[/math] — средняя широта перелёта.

Пример. Определить истинный локсодромический путевой угол [math]\displaystyle{ \alpha }[/math] при полёте из г. Реймса в г. Потсдам.

Решение. Определяем координаты:

 — Реймса [math]\displaystyle{ \varphi_1 = 49^\circ 15' = 2955'; \lambda_1 = 4^\circ 02'= 242'; }[/math]

 — Потсдама [math]\displaystyle{ \varphi_2 = 52^\circ 24' = 3144'; \lambda_2 = 13^\circ 04' = 784'; }[/math]

средняя широта [math]\displaystyle{ \varphi_m= 50^\circ 50' }[/math]; [math]\displaystyle{ \cos 50^\circ 50' = 0{,}6316 }[/math]. Следовательно,

[math]\displaystyle{ \mathrm{tg} \alpha = \frac{784-242} {3144-2955}0{,}6316 = 1{,}806 }[/math],

[math]\displaystyle{ \alpha = 61^\circ }[/math].

Полученный результат будет правильным, если конечная точка маршрута лежит в первой четверти (0 — 90°). Если конечная точка лежит во второй четверти (90° — 180°), искомый путевой угол получают, вычитая полученное число градусов из 180°. Если же конечная точка находится в третьей четверти (180° — 270°), к полученному углу прибавляют 180°, а если в четвёртой четверти (270° — 360°), то полученный угол вычитают из 360°.

Длина локсодромии в км определяется по формулам:

а) Для углов [math]\displaystyle{ \alpha }[/math], близких к 0° или 180°,

[math]\displaystyle{ S \approx \frac{\varphi_2 - \varphi_1} {\cos \alpha} \cdot 1{,}852 }[/math]км,

где [math]\displaystyle{ \varphi_1 }[/math] и [math]\displaystyle{ \varphi_2 }[/math] — широты пунктов вылета и прибытия, выраженные в минутах, или

[math]\displaystyle{ S \approx \frac{\varphi_2 - \varphi_1} {\cos \alpha} \cdot 111{,}18 }[/math]км,

где [math]\displaystyle{ \varphi_1 }[/math] и [math]\displaystyle{ \varphi_2 }[/math] выражены в градусах.

б) Для углов [math]\displaystyle{ \alpha }[/math], близких к 90° или 270°,

[math]\displaystyle{ S \approx \frac {\lambda_2-\lambda_1} {\sin \alpha} \cdot \cos \varphi_m \cdot 1{,}852 }[/math]км.

Разность между длинами локсодромии и ортодромии DS достигает своей максимальной величины при полёте вдоль параллели.

Так, например, длина локсодромии между Реймсом и Потсдамом из предыдущего примера может быть приближённо вычислена по формуле:

[math]\displaystyle{ S \approx \frac{784-242}{\sin 61^\circ} \cdot 0{,}6316 \cdot 1{,}852 \approx 725 }[/math]км.

Формулы в декартовых координатах

Параметрические формулы, задающие локсодрому с путевым углом [math]\displaystyle{ \alpha }[/math] на сфере радиуса [math]\displaystyle{ r }[/math] в декартовой системе координат, имеют вид:

[math]\displaystyle{ x=r\frac{\cos\lambda}{\mathrm{ch}[(\lambda-\lambda_0) \operatorname{ctg} \alpha ]}; }[/math]

[math]\displaystyle{ y=r\frac{\sin\lambda}{\mathrm{ch}[(\lambda-\lambda_0) \operatorname{ctg} \alpha ]}; }[/math]

[math]\displaystyle{ z=r\,\mathrm{th}[(\lambda-\lambda_0) \operatorname{ctg} \alpha ]; }[/math]

где параметр [math]\displaystyle{ \lambda }[/math] меняется от 0 до [math]\displaystyle{ 2\pi }[/math] и является долготой точки. Здесь [math]\displaystyle{ \mathrm{ch} }[/math] и [math]\displaystyle{ \mathrm{th} }[/math] — гиперболические косинус и тангенс.

См. также

• Ортодрома

Ссылки

• Онлайн калькулятор: Путевой угол и расстояние между двумя точками по локсодроме (линии румба)
• Лаксодромия // Военная энциклопедия : [в 18 т.] / под ред. В. Ф. Новицкого … [и др.]. — СПб. ; [М.] : Тип. т-ва И. Д. Сытина, 1911—1915.
• Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Локсодрома (англ.) — биография в архиве MacTutor.