Дельтоида

Не следует путать с дельтоидом.

Дельтоида

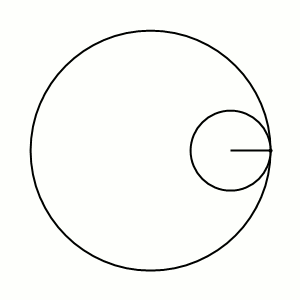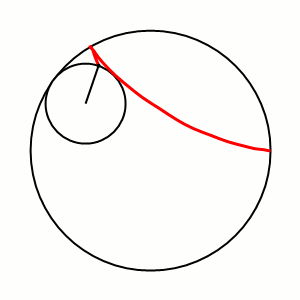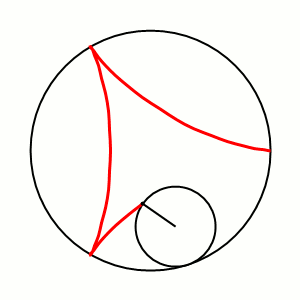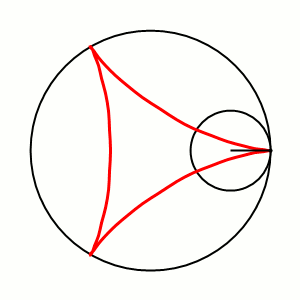
Дельтоида (или кривая Штейнера) — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой.

Дельтоида является частным случаем гипоциклоиды при [math]\displaystyle{ k=3 }[/math].

История

Обычные циклоиды были изучены Галилео Галилеем и Марином Мерсенном (Marin Mersenne) еще в 1599 году, но специальные циклоидальные кривые были впервые рассмотрены Оле Ремерем (Ole Rømer) в 1674 году при изучении лучшей формы зубьев для зубчатых колес. Леонард Эйлер впервые упоминает настоящую дельтоиду в 1745 году в связи с задачей из оптики.

Название кривая получила за сходство с греческой буквой Δ. Её свойства впервые изучались Л. Эйлером в XVIII веке, а затем Я. Штейнером в XIX.

Уравнения

Дельтоида изображена красным цветом.

• Дельтоида может быть представлена (с точностью до вращения и параллельного переноса) следующим параметрическим уравнением:

[math]\displaystyle{ x=(b-a)\cos(t)+a\cos\left(\frac{b-a}at\right) \, }[/math]

[math]\displaystyle{ y=(b-a)\sin(t)-a\sin\left(\frac{b-a}at\right) \, , }[/math]

где a — радиус катящегося круга, b — радиус большего круга, по которому катится вышеупомянутый круг. (На рисунке выше b = 3a.)

• В комплексных координатах оно принимает вид

[math]\displaystyle{ z=2ae^{it}+ae^{-2it} }[/math].

• Неявное уравнение в прямоугольной системе:

[math]\displaystyle{ \textstyle (x^2+y^2)^2+18(x^2+y^2) = 8x^3-24y^2x+27 }[/math]

• Параметрическое:

[math]\displaystyle{ \begin{cases} x=2r\cos{t}+r\cos(2t) \\ y=2r\sin{t}-r\sin(2t) \end{cases} }[/math], где [math]\displaystyle{ t=\frac{\varphi}{3} }[/math] — треть полярного угла.

• В полярных координатах оно принимает вид

[math]\displaystyle{ r^4+18a^2r^2-27a^4=8ar^3\cos 3\theta\,. }[/math]

Свойства

• Кривая имеет три особенности (каспа) соответствующие [math]\displaystyle{ t=0,\, \pm\tfrac{2\pi}{3} }[/math] в параметрическом уравнении выше.
• 3 вершины дельтоиды — это 3 вершины равностороннего треугольника.
• Дельтоида является рациональной кривой нулевого рода.
• Длина пересечения области, ограниченной дельтоидой, с любой её касательной фиксирована и равна [math]\displaystyle{ \tfrac43{\cdot R} }[/math], где [math]\displaystyle{ R }[/math] — радиус неподвижной окружности.
• Дельтоида — алгебраическая кривая 4 порядка.
• Длина кривой [math]\displaystyle{ \textstyle L=\frac{16}{3}R }[/math], где [math]\displaystyle{ R }[/math] — радиус неподвижной окружности.
• Площадь, ограничиваемая дельтоидой, [math]\displaystyle{ \textstyle S=\frac{2}{9}\pi R^2 }[/math].
• Касательные к двум ветвям дельтоиды (на рисунке все три ветви чёрного цвета), проведённые в двух точках концов отрезка касательной к третьей её ветви (именуемых двумя связными точками, они на рисунке синего цвета), пересекаются всегда под прямым углом (на рисунке не показан). Вершина этого прямого угла всегда лежит на окружности малого круга (на том же рисунке малый круг красного цвета и описан красной точкой в середине синего отрезка), касающегося трёх указанных ветвей.

Приложения

Дельтоиды возникают в нескольких областях математики. Например:

• Множество комплексных собственных значений унистохастических (unistochastic) матриц третьего порядка образует дельтоиду.
• Поперечное сечение множества унистохастических (unistochastic) матриц третьего порядка образует дельтоиду.
• Множество возможных следов унитарных матриц, принадлежащих группе SU (3), образует дельтоиду.
• Пересечение двух дельтоид параметризует семейство комплексных матриц Адамара (Complex Hadamard matrix) шестого порядка.
• Все прямые Симсона данного треугольника образуют огибающие в форме дельтоиды. Она известна как дельтоида Штейнера или гипоциклоида Штейнера в честь Якоба Штейнера, который описал форму и симметрию кривой в 1856 году.
• Огибающей для семейства прямых, которые делят площадь треугольника пополам, является кривая, похожая на дельтоиду, с вершинами в серединах трёх медиан. Дуги этой «дельтоиды» являются дугами гиперболы, которые имеют асимптоты, проходящие через стороны треугольника.
• Дельтоида была предложена в качестве решения задачи об иголке.

См. также

• Астроида — гипоциклоида при [math]\displaystyle{ k=4 }[/math].
• Гипоциклоида
• Дельтоид 
• Задача об иголке
• Прямая Симсона
• Циклоида

Литература

• Савёлов А.А. Плоские кривые: Систематика, свойства, применения. Справочное руководство / Под ред. А.П. Нордена. — М.: Физматлит, 1960. — С. 124—129.
• В. Березин. Дельтоида (рус.) // Квант. — 1977. — № 3. — С. 19.
• E. H. Lockwood. Chapter 8: The Deltoid // A Book of Curves (англ.). — Cambridge University Press, 1961.