Овал Кассини

Овалы Кассини (a = 0,6c, 0,8c, c, 1,2c, 1,4c, 1,6c)

Овал Кассини — кривая, являющаяся геометрическим местом точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату некоторого числа [math]\displaystyle{ a }[/math]. Является частным случаем торического сечения и кривой Персея.

Частным случаем овала Кассини при фокусном расстоянии, равном [math]\displaystyle{ 2a }[/math], является лемниската Бернулли.

В новое время кривая была введена (переоткрыта) астрономом Джованни Кассини. Он ошибочно считал, что она точнее определяет орбиту Земли, чем эллипс. Хотя эту линию называют овалом Кассини, она не всегда овальна (см. ниже — Особенности формы).

Вариации (другие случаи)

Кривая постоянной суммы расстояний до двух заданных точек — эллипс, постоянного отношения — окружность Аполлония, постоянной разности — гипербола.

Уравнения

Расстояние между фокусами [math]\displaystyle{ 2c }[/math].

• В прямоугольных координатах:

[math]\displaystyle{ \textstyle (x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4 }[/math]

Вывод

Фокусы — [math]\displaystyle{ F_1(-c;0) }[/math] и [math]\displaystyle{ F_2(c;0) }[/math]. Возьмём произвольную точку [math]\displaystyle{ M(x;y) }[/math], найдём расстояние от фокусов до неё и приравняем его к [math]\displaystyle{ a^2 }[/math]: [math]\displaystyle{ \textstyle \sqrt{(x+c)^2+y^2}\cdot\sqrt{(x-c)^2+y^2}=a^2 }[/math] Возводим в квадрат обе части равенства: [math]\displaystyle{ \textstyle \Big((x+c)^2+y^2\Big)\cdot\Big( (x-c)^2+y^2\Big)=a^4 }[/math] Раскрываем скобки в левой части: [math]\displaystyle{ \textstyle (x^2-c^2)^2+y^4+2y^2(x^2+c^2)=a^4 }[/math] Раскрываем скобки, свёртываем новый квадрат суммы и выносим общий множитель: [math]\displaystyle{ \textstyle (x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4 }[/math]

• Явное уравнение в прямоугольных координатах:

[math]\displaystyle{ \textstyle y=\pm\sqrt{\sqrt{a^4+4c^2x^2}-x^2-c^2} }[/math]

Вывод

[math]\displaystyle{ \textstyle (x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4 }[/math] Возводим в квадрат и раскрываем скобки: [math]\displaystyle{ \textstyle x^4+2x^{2}y^2+y^4-2c^{2}x^2+2c^{2}y^2=a^4-c^4 }[/math] Приводим к виду [math]\displaystyle{ \textstyle y^4+2y^{2}(x^2+c^2)+x^4-2c^{2}x^2-a^4+c^4=0 }[/math] Это квадратное уравнение относительно [math]\displaystyle{ y^2 }[/math]. Решив его, получим [math]\displaystyle{ \textstyle y^2=-(x^2+c^2)\pm\sqrt{a^4+4x^{2}c^2} }[/math] Взяв корень и отбросив вариант с отрицательным вторым слагаемым, получим: [math]\displaystyle{ \textstyle y=\pm\sqrt{\sqrt{a^4+4x^2 c^2}-x^2-c^2} }[/math] где положительный вариант определяет верхнюю половину кривой, отрицательный — нижнюю.

• В полярной системе координат:

[math]\displaystyle{ \rho^4-2c^2\rho^2\cos{2\varphi}=a^4-c^4 }[/math]

Вывод

[math]\displaystyle{ \textstyle (x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4 }[/math] Используя формулы перехода к полярной системе координат [math]\displaystyle{ x=\rho\cos\varphi,\,y=\rho\sin\varphi, }[/math] получим: [math]\displaystyle{ \Big(\rho^2\cos^{2}\varphi+\rho^2\sin^{2}\varphi\Big)^2-2c^2\Big(\rho^2\cos^2\varphi-\rho^2\sin^2\varphi\Big)=a^4-c^4 }[/math] Выносим общие множители и используем тригонометрическое тождество [math]\displaystyle{ \sin^2 \alpha + \cos^2 \alpha = 1 }[/math]: [math]\displaystyle{ \textstyle\rho^4-2c^2\rho^2(cos^2\varphi-\sin^2\varphi)=a^4-c^4 }[/math] Используем ещё одно тождество: [math]\displaystyle{ \cos^2 \alpha - \sin^2 \alpha = cos 2\alpha }[/math]: [math]\displaystyle{ \textstyle\rho^4-2c^2 \rho^2\cos 2\varphi=a^4-c^4 }[/math]

Особенности формы

Меняется параметр [math]\displaystyle{ a }[/math]

Меняется параметр [math]\displaystyle{ c }[/math]

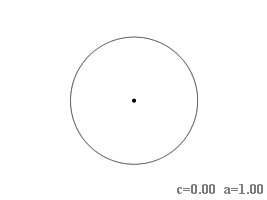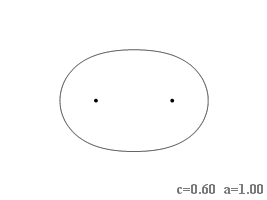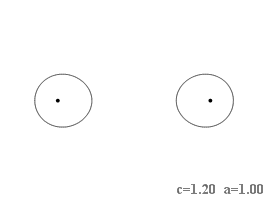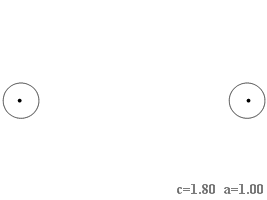
В уравнении кривой содержатся два независимых параметра: [math]\displaystyle{ c }[/math] — половина расстояния между фокусами и [math]\displaystyle{ a }[/math] — корень квадратный из произведения расстояний от фокусов до любой точки кривой. С точки зрения формы наиболее существенно отношение параметров, а не их величины, которые при неизменном отношении определяют лишь размер фигуры. Можно выделить шесть разновидностей формы в зависимости от величины отношения [math]\displaystyle{ \textstyle\frac{c}{a} }[/math]:

• [math]\displaystyle{ \textstyle\frac{c}{a}=\infty }[/math], то есть [math]\displaystyle{ \textstyle a=0 }[/math] при [math]\displaystyle{ \textstyle c\neq 0 }[/math].

Кривая вырождается в две точки, которые совпадают с фокусами. При [math]\displaystyle{ c\to\infty }[/math] форма кривой стремится к двум точкам.

• [math]\displaystyle{ \textstyle 1\lt \frac{c}{a}\lt \infty }[/math], то есть [math]\displaystyle{ \textstyle 0\lt a\lt c }[/math]

Кривая распадается на два отдельных овала, каждый из которых вытянут в направлении другого и по форме напоминает яйцо.

• [math]\displaystyle{ \textstyle\frac{c}{a}=1 }[/math], то есть [math]\displaystyle{ \textstyle a=c }[/math]

Правая часть уравнения в прямоугольных координатах (см. выше) обращается в ноль, и кривая становится лемнискатой Бернулли.

• [math]\displaystyle{ \textstyle \frac{1}{\sqrt{2}}\lt \frac{c}{a}\lt 1 }[/math], то есть [math]\displaystyle{ \textstyle c\lt a\lt c\sqrt{2} }[/math]

У кривой появляются четыре симметричные точки перегиба (по одной в каждой координатной четверти). Кривизна в точках пересечения с осью [math]\displaystyle{ OY }[/math] стремится к нулю, когда [math]\displaystyle{ a }[/math] стремится к [math]\displaystyle{ c }[/math] и к бесконечности, когда [math]\displaystyle{ a }[/math] стремится к [math]\displaystyle{ c\sqrt{2} }[/math].

• [math]\displaystyle{ \textstyle 0\lt \frac{c}{a}\leqslant\frac{1}{\sqrt{2}} }[/math], то есть [math]\displaystyle{ \textstyle a\geqslant c\sqrt{2} }[/math]

Кривая становится овалом, то есть выпуклой замкнутой кривой.

• [math]\displaystyle{ \textstyle\frac{c}{a}=0 }[/math], то есть [math]\displaystyle{ \textstyle c=0 }[/math] при [math]\displaystyle{ \textstyle a\neq 0 }[/math]

По мере увеличения [math]\displaystyle{ a }[/math] (то есть стремления отношения [math]\displaystyle{ \textstyle\frac{c}{a} }[/math] к нулю) кривая стремится к окружности радиуса [math]\displaystyle{ a }[/math]. Если [math]\displaystyle{ c=0 }[/math], то отношение [math]\displaystyle{ \textstyle\frac{c}{a} }[/math] достигает нуля, и в этом случае кривая вырождается в окружность.

Свойства

Чёрная окружность — множество максимумов и минимумов; синяя лемниската — множество точек перегиба

• Овал Кассини — алгебраическая кривая четвёртого порядка.
• Она симметрична относительно середины отрезка между фокусами.
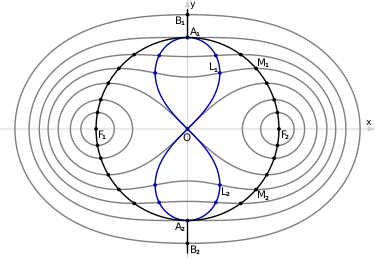
• При [math]\displaystyle{ 0\lt a\lt c\sqrt{2} }[/math] имеет два абсолютных максимума и два минимума:

[math]\displaystyle{ \begin{cases}x=\pm\frac{\sqrt{4c^4-a^4}}{2c} \\ y=\pm\frac{a^2}{2c}\end{cases} }[/math]

Геометрическое место точек абсолютных максимумов и минимумов — окружность радиуса [math]\displaystyle{ c }[/math] с центром в середине отрезка между фокусами.

• При [math]\displaystyle{ c\lt a\leqslant c\sqrt{2} }[/math] кривая имеет четыре точки перегиба. Их полярные координаты:

[math]\displaystyle{ \begin{cases}\rho=\sqrt[4]{\frac{a^4-c^4}{3}} \\ \cos 2\varphi =-\sqrt{\frac{1}{3}\left (\frac{a^4}{c^4}-1\right )}\end{cases} }[/math]

Геометрическое место точек перегиба — лемниската с вершинами [math]\displaystyle{ \left (0;\pm c\right ) }[/math].

• Радиус кривизны для представления в полярных координатах:

[math]\displaystyle{ R=\frac{a^2\rho}{\rho^2+c^2\cos{2\varphi}}=\frac{2a^2\rho^3}{c^4-a^4+3\rho^4} }[/math]

Применение

При двухпозиционной радиолокации областью обнаружения цели является фигура, ограниченная овалом Кассини, если принять в качестве одного его фокуса позицию источника излучения, а другого — позицию приёмника. Аналогично, в астрономии при наблюдении, например, астероидов, светящих отражённым светом Солнца, условия их обнаружения при заданной чувствительности телескопа описываются формулой овала Кассини. В этом случае границей обнаружимости будет поверхность, образованная вращением овала вокруг оси, соединяющей Солнце и наблюдателя.

Овалы Кассини на торе (тороиде)

Овалы Кассини (синие) как плоские сечения тора (на правой стороне от оси тора)

Овалы Кассини появляются как плоские сечения тора, но только тогда, когда секущая плоскость параллельна оси тора, а её расстояние до оси равно радиусу образующей окружности (см. рисунок).

Обобщения

• Овал Кассини является частным случаем лемнискаты.

• Овал Кассини — частный случай кривой Персея.

В частности, уравнение кривой Персея в декартовой системе координат

[math]\displaystyle{ (x^2 + y^2)^2 = ax^2 + by^2 + c }[/math].

при [math]\displaystyle{ a=-b=2c^2, c=a^4-c^4 }[/math] переходит в уравнение овала Кассини

[math]\displaystyle{ \textstyle (x^2+y^2)^2-2c^2(x^2-y^2)=a^4-c^4 }[/math]

См. также

• Лемниската Бута
• Лемниската Бернулли
• Плоская кривая
• Алгебраическая кривая
• Многофокусная алгебраическая кривая
• Овал Декарта

Литература

• Математическая энциклопедия (в 5 томах), Москва, «Советская Энциклопедия», 1982, т. 2 Д — Коо, с. 759.
• Маркушевич А. И. Замечательные кривые, Популярные лекции по математике Архивная копия от 26 августа 2017 на Wayback Machine, выпуск 4, Гостехиздат 1952 г., 32 с.