Эллиптический интеграл
Эллипти́ческий интегра́л — некоторая функция [math]\displaystyle{ f }[/math] над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
- [math]\displaystyle{ f(x) = \int \limits_{c}^{x}\!R(t,\;P(t))\,dt }[/math],
где [math]\displaystyle{ R }[/math] — рациональная функция двух аргументов, [math]\displaystyle{ P }[/math] — квадратный корень из многочлена 3-й или 4-й степени, не имеющего кратных корней, [math]\displaystyle{ c }[/math] — некоторая константа из поля, где определена функция.
В общем случае эллиптический интеграл не может быть формально выражен в элементарных функциях. Исключением являются случаи, когда [math]\displaystyle{ P }[/math] имеет кратные корни или когда многочлены в [math]\displaystyle{ R(x,\;y) }[/math] не содержат нечётных степеней [math]\displaystyle{ y }[/math].
Однако для каждого эллиптического интеграла существуют формулы приведения его к сумме элементарных функций и от одного до трёх нормальных эллиптических интегралов, называемых эллиптическими интегралами 1-го, 2-го и 3-го рода).
История
В интегральном исчислении эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно, а позднее — Леонардом Эйлером.
Обозначения
Эллиптические интегралы часто представляют в виде функции ряда различных аргументов. Эти различные аргументы полностью эквивалентны (они дают одни и те же интегралы), но может возникнуть путаница, связанная с их различным происхождением. В большинстве работ авторы придерживаются канонического наименования. Прежде чем определить сами интегралы, необходимо ввести наименования для аргументов:
- [math]\displaystyle{ \alpha }[/math] — модулярный угол (иногда модулярный угол обозначается лигатурой [math]\displaystyle{ o\!\varepsilon }[/math]);
- [math]\displaystyle{ k=\sin \alpha }[/math] — модуль эллиптического интеграла;
- [math]\displaystyle{ m=k^2=\sin^2 \alpha }[/math] — параметр.
Следует отметить, что нормальные эллиптические интегралы Лежандра, как полные, так и неполные, являются чётными функциями модуля [math]\displaystyle{ k }[/math] (и модулярного угла [math]\displaystyle{ \alpha }[/math]). Их область определения [math]\displaystyle{ -1 \le k \le +1. }[/math]
Иногда, преимущественно в советской научной литературе, под параметром эллиптического интеграла подразумевают характеристику нормального эллиптического интеграла Лежандра 3-го рода (напр., Корн Г., Корн Т. «Справочник по математике для научных работников и инженеров»).
Заметим, что представленные выше величины определяются одна через другую; определение одной из них задаёт и две остальные.
Эллиптический интеграл зависит также и от другого параметра, который, как и предыдущий, можно ввести несколькими способами:
- [math]\displaystyle{ x=\sin \varphi= \operatorname{sn} u, }[/math] где [math]\displaystyle{ \operatorname{sn} }[/math] — эллиптическая функция Якоби;
- [math]\displaystyle{ \varphi = \arcsin x = \operatorname{am} u }[/math] — амплитуда;
Определение одного из этих параметров определяет остальные. Таким образом, они могут использоваться вперемешку. Заметим, что [math]\displaystyle{ u }[/math] зависит также и от [math]\displaystyle{ m }[/math]. Несколько дополнительных уравнений связывают [math]\displaystyle{ u }[/math] с другими параметрами:
- [math]\displaystyle{ \cos \varphi = \operatorname{cn} u }[/math]
и
- [math]\displaystyle{ \sqrt{1-m\sin^2 \varphi} = \operatorname{dn} u. }[/math]
Последнее иногда называется дельта амплитуда и записывается как
- [math]\displaystyle{ \Delta(\varphi)=\operatorname{dn} u. }[/math]
Иногда в литературе ссылаются на дополнительный параметр, дополнительный модуль или дополнительный модулярный угол. Их вводят следующим способом:
- [math]\displaystyle{ m_1\,=\,1 - m }[/math] — дополнительный параметр;
- [math]\displaystyle{ k'=\sqrt{1-k^2} }[/math] — дополнительный модуль;
- [math]\displaystyle{ {k'}^2=m_1 }[/math] — дополнительный модулярный угол.
Нормальный эллиптический интеграл 1-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 1-го рода [math]\displaystyle{ F }[/math] определяется как
- [math]\displaystyle{ F(\varphi,\; k ) = \int\limits_0^\varphi\!\frac{d\theta}{\sqrt{1 - k^2 \sin^2\theta}} }[/math],
или, в форме Якоби,
- [math]\displaystyle{ F(x,\;k) = \int\limits_{0}^{x}\!\frac{dz}{\sqrt{(1-z^2)(1-k^2 z^2)} } }[/math].
Обозначения эллиптических интегралов не являются универсально общепринятыми. Следует различать такие разделители между переменной и параметром, как «\», «|» и «,». Там, где в качестве разделителя используется вертикальная черта, за ней ставится параметр интеграла, тогда как за обратной косой чертой ставится модулярный угол. В частности, верно соотношение
- [math]\displaystyle{ F(\varphi,\;\sin \alpha) = F(\varphi\mid\sin^2 \alpha) = F(\varphi\setminus \alpha ) }[/math].
Частные случаи
- [math]\displaystyle{ F(\varphi \setminus 0) = \varphi }[/math];
- [math]\displaystyle{ F(i\varphi \setminus 0) = i\varphi }[/math];
- [math]\displaystyle{ F(\varphi \setminus 90^{\circ}) = \ln\left(\operatorname{sec}\varphi +\operatorname{tg}\varphi\right) = \ln\operatorname{tg}\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) }[/math];
- [math]\displaystyle{ F(i\varphi \setminus 90^\circ) = i\,\operatorname{arctg}\left(\operatorname{sh}\varphi\right) }[/math];
Нормальный эллиптический интеграл 2-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 2-го рода E определяется как
- [math]\displaystyle{ E(\varphi,\; k) = \int\limits_0^\varphi\!\sqrt{1 - k^2 \sin^2 \theta}\,d\theta }[/math]
или, используя подстановку [math]\displaystyle{ x=\sin\varphi, }[/math]
- [math]\displaystyle{ E(x,\;k) = \int \limits_{0}^{x}\!\frac{\sqrt{1 - k^2 z^2}}{\sqrt{1 - z^2}}\,dz. }[/math]
Частные случаи
- [math]\displaystyle{ E(\varphi, 0) = \varphi }[/math];
- [math]\displaystyle{ E(i\varphi, 0) = i\varphi }[/math];
- [math]\displaystyle{ E(\varphi, 1) = \sin\varphi }[/math];
- [math]\displaystyle{ E(i\varphi, 1) = i\,\operatorname{sh}\varphi }[/math].
Нормальный эллиптический интеграл 3-го рода (неполный)
Нормальный эллиптический интеграл Лежандра 3-го рода [math]\displaystyle{ \Pi }[/math] определяется как
- [math]\displaystyle{ \Pi(c;\; \varphi,\; k) = \int \limits_{0}^{\varphi}\!\frac{d\theta}{(1+c \sin^2 \theta) \sqrt{1-k^2\sin^2\theta}} }[/math]
или
- [math]\displaystyle{ \Pi(c;\; x,\; k) = \int \limits_{0}^{x}\!\frac{dx}{(1+cx^2)\sqrt{(1-k^2 x^2)(1-x^2)}} }[/math]
Число [math]\displaystyle{ c }[/math] называется характеристикой и может принимать любое значение, независимо от остальных аргументов. Свойства эллиптического интеграла 3-го рода существенно зависят от величины характеристики. Заметим, что значение интеграла [math]\displaystyle{ \Pi(-1;\; \pi/2 \mid m) }[/math] стремится к бесконечности для любых [math]\displaystyle{ m }[/math].
Гиперболический случай
(0 < c < m)
Введём дополнительные обозначения:
- [math]\displaystyle{ \varepsilon = \operatorname{arcsin}\,\sqrt{\frac{n}{\sin^2\alpha}}, \qquad 0\leqslant\varepsilon\leqslant\frac{\pi}{2} }[/math];
- [math]\displaystyle{ \beta = \frac{\pi\,F(\varepsilon \setminus \alpha)}{2\,K(\alpha)} }[/math];
- [math]\displaystyle{ q=q(\alpha) }[/math];
- [math]\displaystyle{ \nu = \frac{\pi\,F(\varphi \setminus \alpha)}{2\,K(\alpha)} }[/math];
- [math]\displaystyle{ \delta_1=\sqrt{ \frac{c} {(1-c)(\sin^2\alpha - c)} } }[/math];
- [math]\displaystyle{ K(\alpha) }[/math] — полный нормальный эллиптический интеграл Лежандра 1-го рода.
Тогда можно записать интеграл через тета-функции Якоби:
- [math]\displaystyle{ \Pi(c;\; \varphi\setminus\alpha) = \delta_1\left(-\frac{1}{2}\,\ln\frac{\vartheta_4(\nu+\beta)}{\vartheta_4(\nu-\beta)} + \nu\,\frac{\vartheta_1'(\beta)}{\vartheta_1(\beta)}\right), }[/math]
где
- [math]\displaystyle{ \frac{1}{2}\,\ln\frac{\vartheta_4(\nu+\beta)}{\vartheta_4(\nu-\beta)} = 2 \sum_{s=1}^{\infty} \frac{q^s}{s(1-q^{2s})}\sin{2s\nu}\,\sin\,{2s\beta} }[/math]
и
- [math]\displaystyle{ \frac{\vartheta_1'(\beta)}{\vartheta_1(\beta)} = \operatorname{ctg}\,\beta + 4\sum_{s=1}^{\infty} \frac{q^{2s}}{1 - 2q^{2s}\cos{2\beta} + q^{4s}}\sin{2\beta}. }[/math]
(c > 1)
С помощью подстановки [math]\displaystyle{ C = \frac{\sin^2\alpha}{c} }[/math] этот случай сводится к предыдущему, так как [math]\displaystyle{ 0 \lt C \lt \sin^2\alpha. }[/math]
Введём дополнительно величину
- [math]\displaystyle{ p_1 = \sqrt{(c-1)\left(1 - \frac{\sin^2\alpha}{c}\right)}. }[/math]
Тогда:
- [math]\displaystyle{ \Pi(c;\; \varphi\setminus\alpha) = - \Pi(C;\; \varphi\setminus\alpha) + F(\varphi \setminus \alpha) + \frac{1}{2p_1}\ln\left(\frac{\Delta(\varphi) + p_1\operatorname{tg}\,\varphi}{\Delta(\varphi) - p_1\operatorname{tg}\,\varphi}\right). }[/math]
Круговой случай
(m < c < 1)
Введем дополнительные обозначения:
- [math]\displaystyle{ \varepsilon = \operatorname{arcsin}\,\sqrt{\frac{1-n}{\cos^2\alpha}}, \qquad 0\leqslant\varepsilon\leqslant\frac{\pi}{2}; }[/math]
- [math]\displaystyle{ \beta = \frac{\pi\,F(\varepsilon \setminus 90^{\circ}-\alpha)}{2\,K(\alpha)}; }[/math]
- [math]\displaystyle{ q=q(\alpha); }[/math]
- [math]\displaystyle{ \nu = \frac{\pi\,F(\varphi \setminus \alpha)}{2\,K(\alpha)}; }[/math]
- [math]\displaystyle{ \delta_2 = \sqrt{\frac{c}{(1-c)(c - \sin^2\alpha)}}. }[/math]
Тогда эллиптический интеграл равен:
- [math]\displaystyle{ \Pi(c;\; \varphi\setminus\alpha) = \delta_2(\lambda - 4\mu\nu), }[/math]
где
- [math]\displaystyle{ \lambda = \operatorname{arctg}\,(\operatorname{th}\,\beta\,\operatorname{tg}\,\nu) + 2 \sum_{s=1}^{\infty} \frac{(-1)^{s-1}}{s}\frac{q^{2s}}{1-q^{2s}}\sin{2s\nu}\,\operatorname{sh}\,{2s\beta} }[/math]
и
- [math]\displaystyle{ \mu=\dfrac{\sum\limits_{s=1}^{\infty} sq^{s^2}\,\operatorname{sh}\,{2s\beta}}{1+\sum\limits_{s=1}^{\infty} q^{s^2}\,\operatorname{ch}\,{2s\beta}} }[/math]
(c < 0)
С помощью подстановки [math]\displaystyle{ C = \frac{\sin^2\alpha - c}{1-c} }[/math] этот случай сводится к предыдущему, так как [math]\displaystyle{ \sin^2\alpha\ \lt C \lt 1. }[/math]
Введем дополнительно величину
- [math]\displaystyle{ p_2 = \sqrt{\frac{-c\,(\sin^2\alpha-c)}{1-c}}. }[/math]
Тогда:
- [math]\displaystyle{ \sqrt{(1-c)\left(1-\frac{\sin^2\alpha}{c}\right)}\,\Pi(c;\; \varphi \setminus \alpha) = \sqrt{(1-C)\left(1-\frac{\sin^2\alpha}{C}\right)}\,\Pi(C;\; \varphi \setminus \alpha)\, +\, \frac{\sin^2\alpha\,F(\varphi \setminus \alpha)}{p_2}\, +\, \operatorname{arctg}\,\left(\frac{p_2}{2}\frac{\sin{2\varphi}}{\Delta(\varphi)}\right) }[/math]
Полный нормальный эллиптический интеграл Лежандра 1-го рода

В случае, если амплитуда [math]\displaystyle{ \varphi }[/math] нормального эллиптического интеграла Лежандра 1-го рода равна [math]\displaystyle{ \pi/2 }[/math], он называется полным нормальным эллиптическим интегралом Лежандра 1-го рода:
- [math]\displaystyle{ K(k) = \int \limits_{0}^{\pi/2}\!\frac{d\varphi}{\sqrt{1-k^2 \sin^2\varphi}} = F(\pi/2,\; k) }[/math]
или
- [math]\displaystyle{ K(k) = \int \limits_{0}^{1}\!\frac{dx}{\sqrt{(1-x^2)(1-k^2 x^2)}}. }[/math]
Полный эллиптический интеграл 1-го рода можно представить в виде степенного ряда:
- [math]\displaystyle{ K(k) = \frac{\pi}{2} \sum_{n=0}^{\infty} \left(\frac{(2n)!}{2^{2 n} n!^2}\right)^2 k^{2n}, }[/math]
что эквивалентно выражению
- [math]\displaystyle{ K(k) = \frac{\pi}{2}\left(1 + \left(\frac{1}{2}\right)^2 k^{2} + \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 k^{4} + \ldots + \left(\frac{(2n - 1)!!}{(2n)!!}\right)^2 k^{2n} + \ldots \right), }[/math]
где [math]\displaystyle{ n!! }[/math] обозначает двойной факториал.
Полный эллиптический интеграл 1-го рода можно записать через гипергеометрическую функцию следующим образом:
- [math]\displaystyle{ K(k) = \frac{\pi}{2} \,_2F_1 \left(\frac{1}{2},\; \frac{1}{2};\; 1;\; k^2\right). }[/math]
Частные случаи
- [math]\displaystyle{ K(0) = \frac{\pi}{2}. }[/math]
- [math]\displaystyle{ K(1) = \infty. }[/math]
- [math]\displaystyle{ K\left(\frac{\sqrt{2}}{2}\right) = \frac{\Gamma\left(\frac{1}{4}\right)^2}{4 \sqrt{\pi}}. }[/math]
- [math]\displaystyle{ K\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right) = \frac{2^{-\frac{7}{3}} 3^{\frac{1}{4}} \Gamma\left(\frac{1}{3}\right)^3}{\pi}. }[/math]
- [math]\displaystyle{ K\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) = \frac{2^{-\frac{7}{3}} 3^{\frac{3}{4}} \Gamma\left(\frac{1}{3}\right)^3}{\pi}. }[/math]
- [math]\displaystyle{ \operatorname{sn}\,K = \sin{\frac{\pi}{2}} = 1. }[/math]
- [math]\displaystyle{ \operatorname{cn}\,K = \cos{\frac{\pi}{2}} = 0. }[/math]
- [math]\displaystyle{ \operatorname{dn}\,K = \sqrt{1-k^2} = k'. }[/math]
Производная полного эллиптического интеграла 1-го рода
- [math]\displaystyle{ \frac{\mathrm{d}K(k)}{\mathrm{d}k} = \frac{E(k)}{k(1-k^2)}-\frac{K(k)}{k}, }[/math]
где [math]\displaystyle{ E(k) }[/math] — полный нормальный эллиптический интеграл Лежандра 2-го рода, определённый в следующем разделе.
Дифференциальное уравнение
Полный эллиптический интеграл 1-го рода является решением дифференциального уравнения
- [math]\displaystyle{ \frac{d}{dk}\left(k\left(1-k^2\right)\frac{dK(k)}{dk}\right)=k K(k). }[/math]
Вторым решением этого уравнения является [math]\displaystyle{ K\left(\sqrt{1-k^2}\right). }[/math]
Полный нормальный эллиптический интеграл Лежандра 2-го рода
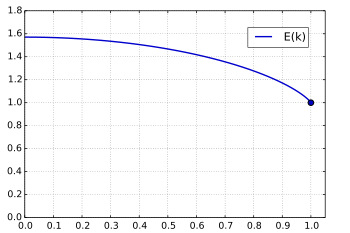
В случае, если амплитуда [math]\displaystyle{ \varphi }[/math] нормального эллиптического интеграла Лежандра 2-го рода равна [math]\displaystyle{ \pi/2 }[/math], он называется полным нормальным эллиптическим интегралом Лежандра 2-го рода:
- [math]\displaystyle{ E(k) = \int \limits_{0}^{\pi/2}\!\sqrt {1-k^2 \sin^2\varphi}\,d\varphi = E(\pi/2,\; k) }[/math]
или
- [math]\displaystyle{ E(k) = \int \limits_{0}^{1}\,\frac{\sqrt{1-k^2 x^2}}{\sqrt{1-x^2}}\,dx. }[/math]
Полный эллиптический интеграл 2-го рода можно представить в виде степенного ряда:
- [math]\displaystyle{ E(k) = \frac{\pi}{2} \sum_{n=0}^{\infty} \left(\frac{(2n)!}{2^{2 n} n!^2}\right)^2 \frac{k^{2n}}{1-2 n}, }[/math]
что эквивалентно выражению
- [math]\displaystyle{ E(k) = \frac{\pi}{2}\left(1 - \left(\frac{1}{2}\right)^2 \frac{k^2}{1} - \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 \frac{k^4}{3} - \ldots - \left(\frac{(2n - 1)!!}{(2n)!!}\right)^2 \frac{k^{2n}}{2 n-1} - \ldots \right). }[/math]
Полный эллиптический интеграл 2-го рода можно записать через гипергеометрическую функцию следующим образом:
- [math]\displaystyle{ E(k) = \frac{\pi}{2} \,_2F_1 \left(\frac{1}{2},\; -\frac{1}{2};\; 1;\; k^2\right). }[/math]
Частные случаи
- [math]\displaystyle{ E\left(0\right) = \frac{\pi}{2}. }[/math]
- [math]\displaystyle{ E\left(1\right) = 1. }[/math]
- [math]\displaystyle{ E\left(\frac{\sqrt{2}}{2}\right) = \pi^{\frac{3}{2}} \Gamma\left(\frac{1}{4}\right)^{-2}+\frac{\Gamma\left(\frac{1} {4}\right)^2}{8 \sqrt \pi}. }[/math]
- [math]\displaystyle{ E\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right) = 2^{\frac{1}{3}} 3^{-\frac{3}{4}} \pi^2 \Gamma\left(\frac{1}{3}\right)^{-3} + 2^{-\frac {10}{3}} 3^{-\frac {1}{4}} \frac{\sqrt{3} + 1}{\pi} \Gamma\left(\frac{1}{3}\right)^3. }[/math]
- [math]\displaystyle{ E\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right) = 2^{\frac 1 3} 3^{-\frac{1}{4}} \pi^2 \Gamma\left(\frac 1 3\right)^{-3} + 2^{-\frac {10}{3}} 3^{\frac{1}{4}} \frac{\sqrt{3} - 1}{\pi} \Gamma\left(\frac{1}{3}\right)^3. }[/math]
Производная полного эллиптического интеграла 2-го рода
- [math]\displaystyle{ \frac{\mathrm{d}E(k)}{\mathrm{d}k}=\frac{E(k)-K(k)}{k}. }[/math]
Дифференциальное уравнение
Полный эллиптический интеграл 2-го рода является решением дифференциального уравнения
- [math]\displaystyle{ \left(k^2-1\right) \frac {d} {dk} \left( k \;\frac {dE(k)} {dk} \right) = k E(k). }[/math]
Вторым решением этого уравнения является функция [math]\displaystyle{ E\left(\sqrt{1-k^2}\right) - K\left(\sqrt{1-k^2}\right). }[/math]
Полный нормальный эллиптический интеграл Лежандра 3-го рода
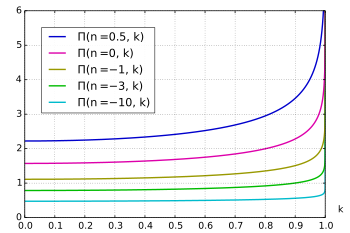
Аналогично полным эллиптическим интегралам 1-го и 2-го рода можно ввести полный эллиптический интеграл 3-го рода:
- [math]\displaystyle{ \Pi(c,\; k) = \Pi(c;\; \pi/2,\; k) = \int \limits_{0}^{\pi/2}\!\frac{d\varphi}{(1+c \sin^2 \varphi) \sqrt{1-k^2\sin^2\varphi}} }[/math]
или
- [math]\displaystyle{ \Pi(c,\; k) = \Pi(c;\; 1,\; k) = \int \limits_{0}^{1}\!\frac{dx}{(1+cx^2)\sqrt{(1-k^2 x^2)(1-x^2)}}. }[/math]
Гиперболический случай
(0 < c < m)
- [math]\displaystyle{ \Pi(c \setminus \alpha) = K(\alpha) + \delta_1K(\alpha)\Zeta(\varepsilon \setminus \alpha) }[/math],
где [math]\displaystyle{ \Zeta(\varepsilon \setminus \alpha) }[/math] — дзета-функция Якоби.
(c > 1)
- [math]\displaystyle{ \Pi(c \setminus \alpha) = K(\alpha) - \Pi(C \setminus \alpha). }[/math]
Круговой случай
(m < c < 1)
- [math]\displaystyle{ \Pi(c \setminus \alpha) = K(\alpha) + \frac{1}{2}\pi\delta_2\left(1-\Lambda_0(\varepsilon \setminus \alpha)\right), }[/math]
где [math]\displaystyle{ \Lambda_0(\varepsilon \setminus \alpha) }[/math] — лямбда-функция Хеймана.
(c < 0)
- [math]\displaystyle{ \Pi(c \setminus \alpha) = -\frac{c\cos^2\alpha\, \Pi(C \setminus \alpha)}{(1-c)(\sin^2\alpha-n)} + \frac{\sin^2\alpha}{\sin^2\alpha - c}K(\alpha). }[/math]
Частные производные
- [math]\displaystyle{ \begin{align} \frac{\partial\Pi(c,k)}{\partial c}&=\frac{1}{2\left(k^2-c\right)(c-1)}\left(E(k)+\frac{1}{c}\left(k^2-c\right)K(k)+\frac{1}{c}\left(c^2-k^2\right)\Pi(c,k)\right). \\[10px] \frac{\partial\Pi(c,k)}{\partial k}&=\frac{k}{c-k^2}\left(\frac{E(k)}{k^2-1}+\Pi(c,k)\right). \end{align} }[/math]
Дополнительные эллиптические интегралы (неполные)
Дзета-функция Якоби
- [math]\displaystyle{ Z(\varphi\setminus\alpha) = E(\varphi\setminus\alpha) - \frac{E(\alpha)F(\varphi\setminus\alpha)}{K(\alpha)}; }[/math]
Лямбда-функция Хеймана
- [math]\displaystyle{ \Lambda_0(\varphi\setminus\alpha) = \frac{F(\varphi\setminus 90^{\circ} - \alpha)}{K'(\alpha)}+\frac{2}{\pi}K(\alpha)\,Z(\varphi\setminus 90^{\circ} - \alpha) }[/math]
или
- [math]\displaystyle{ \Lambda_0(\varphi\setminus\alpha) = \frac{2}{\pi}\left(K(\alpha)\,E(\varphi\setminus 90^{\circ} - \alpha)-\left(K(\alpha) - E(\alpha)\right)\,F(\varphi\setminus 90^{\circ} - \alpha)\right). }[/math]
См. также
- Эллиптические функции
- Эллиптическая кривая
- Специальные функции
- Аппроксимации эллиптических интегралов
Литература
- Бобылёв Д. К. Эллиптические интегралы и функции // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки
- Шаблон:АбрамовицСтиган
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1977.
- Бейтмен Г. Эрдейи А. Высшие трансцендентные функции. — Т. 3 (гл. 13).
- Ахиезер Н. И. Элементы теории эллиптических функций. (гл. 3, 7).
- Эллиптические функции (недоступная ссылка), Процедуры для Matlab.