Алгебраическая кривая

Кубика Чирнгауза — алгебраическая кривая третьего порядка.

Алгебраическая кривая, или плоская алгебраическая кривая, — это результат отображения множества нулей многочлена с двумя переменными на плоскость в виде точек. Степень данного многочлена называют степенью, или порядком, алгебраической кривой. Такие кривые с первой по восьмую степень соответственно называют прямыми, кониками, кубиками, квартиками, пентиками, секстиками, септиками, октиками. Например, единичная окружность — это коника, алгебраическая кривая второй степени. Она задаётся уравнением x² + y² = 1, где степень многочлена x² + y² − 1 равна двум.

По многим техническим причинам удобно рассматривать не только вещественные, но и комплексные корни соответствующего многочлена, а также обобщить определение на случай произвольного основного поля.

В алгебраической геометрии плоская аффинная алгебраическая кривая над полем k определяется как множество точек K², являющихся корнями многочлена от двух переменных с коэффициентами в k, где K — алгебраическое замыкание поля k. Точки этой кривой, все координаты которых лежат в k, называются k-точками. Например, точка [math]\displaystyle{ (2,\sqrt {-3}) }[/math] принадлежит рассмотренной выше единичной окружности, однако не принадлежит её действительной части. Многочлен x² + y² + 1 задаёт алгебраическую кривую, действительная часть которой пуста.

Более обобщённо можно рассматривать алгебраические кривые, которые содержатся не в плоскости, а в пространстве с большим числом измерений или в проективном пространстве. Оказывается, что многие свойства алгебраической кривой не зависят от выбора конкретного вложения в некоторое пространство, что приводит к общему определению алгебраической кривой: Алгебраическая кривая — это алгебраическое многообразие размерности 1. Это определение можно переформулировать так: алгебраическая кривая — это алгебраическое многообразие, все алгебраические подмногообразия которого состоят из одной точки.

Примеры алгебраических кривых

Рациональные кривые

Рациональная кривая, также известная как уникурсальная кривая, — это кривая, бирационально эквивалентная аффинной прямой (или проективной прямой); другими словами, кривая, допускающая рациональную параметризацию.

Более конкретно, рациональная кривая в n-мерном пространстве может быть параметризована (за исключением некоторого числа изолированных «особых точек») при помощи n рациональных функций от единственного параметра t.

Любое коническое сечение над полем рациональных чисел, содержащее хотя бы одну рациональную точку, является рациональной кривой. Её можно параметризовать, проведя через рациональную точку прямую с произвольным угловым коэффициентом t и сопоставив данному t вторую точку пересечения прямой и коники (их не может быть больше двух).

Эллипс. x² + xy + y² = 1

Например, рассмотрим эллипс x² + xy + y² = 1 с рациональной точкой (−1, 0). Проведя через неё прямую y = t(x + 1), подставив выражение y через x в уравнение и решив относительно x, получим уравнения

[math]\displaystyle{ x = \frac{1-t^2}{1+t+t^2}, }[/math]

[math]\displaystyle{ y=t(x+1)=\frac{t(t+2)}{1+t+t^2}\,, }[/math]

задающие рациональную параметризацию эллипса. В таком виде представимы все точки эллипса, кроме точки (−1, 0); можно сопоставить ей t = ∞, то есть параметризовать эллипс проективной прямой.

Эту рациональную параметризацию можно рассматривать как параметризацию «эллипса в проективном пространстве», перейдя к однородным координатам, то есть заменив t на T/U, а x, y — на X/Z, Y/Z соответственно. Параметризация эллипса X² + XY + Y² = Z² проективной прямой примет следующий вид:

[math]\displaystyle{ X=U^2-T^2,\quad Y=T\,(T+2\,U),\quad Z=T^2+TU+U^2. }[/math]

Эллиптические кривые

Рациональные кривые (над алгебраически замкнутым полем) — это в точности алгебраические кривые рода 0 (см. ниже), в этой терминологии эллиптические кривые — это кривые рода 1 с рациональной точкой. Любая такая кривая может быть представлена как кубика без особенностей.

Эллиптическая кривая несёт на себе структуру абелевой группы. Сумма трёх точек на кубике равна нулю тогда и только тогда, когда эти точки коллинеарны.

Пересечение двух коник является кривой четвёртого порядка рода 1, а значит, эллиптической кривой, если содержит хотя бы одну рациональную точку. В противном случае пересечение может быть рациональной кривой четвёртого порядка с особенностями, или быть разложимым на кривые меньшего порядка (кубика и прямая, две коники, коника и две прямые или четыре прямые).

Связь с полями функций

Изучение алгебраических кривых может быть сведено к изучению неприводимых кривых (то есть не раскладывающихся в объединение двух меньших кривых). Каждой такой кривой можно сопоставить поле рациональных функций на ней; оказывается, что кривые бирационально эквивалентны тогда и только тогда, когда их поля функций изоморфны. Это значит, что категория алгебраических кривых и рациональных отображений двойственна категории одномерных полей алгебраических функций, то есть полей, являющихся алгебраическими расширениями поля [math]\displaystyle{ k(x) }[/math].

Комплексные кривые как действительные поверхности

Комплексная алгебраическая кривая, вложенная в аффинное или проективное пространство, имеет топологическую размерность 2, другими словами, является поверхностью. В частности, комплексная алгебраическая кривая без особенностей является двумерным ориентируемым многообразием.

Топологический род этой поверхности совпадает с родом алгебраической кривой (который можно вычислить алгебраическими способами). Если проекция кривой без особенностей на плоскость является алгебраической кривой степени d с простейшими особенностями (обыкновенными двойными точками), то исходная кривая имеет род (d − 1)(d − 2)/2 − k, где k — число этих особенностей.

Изучение компактных римановых поверхностей состоит фактически в изучении комплексных алгебраических кривых без особенностей, рассматриваемых как поверхности с дополнительной аналитической структурой. Более точно, следующие категории эквивалентны:

• Категория проективных алгебраических кривых без особенностей (с рациональными отображениями в качестве морфизмов).
• Категория компактных римановых поверхностей и голоморфных функций.

Классификация особенностей

x³ − y² = 0

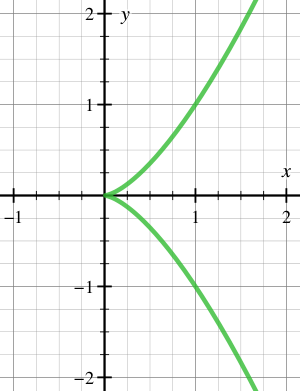
Особые точки включают в себя несколько типов точек, в которых кривая «пересекает сама себя», а также различные типы точек возврата. Например, на рисунке показана кривая x³ − y² = 0 с точкой возврата в начале координат.

Особые точки можно классифицировать по их инвариантам. Например, особую точку с дельта-инвариантом δ можно интуитивно описать как точку, в которой встречаются сразу δ «самопересечений». В случае точки P на неприводимой кривой δ можно вычислить как длину модуля [math]\displaystyle{ \widetilde{\mathcal{O}_P} / \mathcal{O}_P }[/math], где [math]\displaystyle{ \mathcal{O}_P }[/math] — локальное кольцо в точке P и [math]\displaystyle{ \widetilde{\mathcal{O}_P} }[/math] — его целое замыкание. Вычисление дельта-инвариантов всех особых точек позволяет вычислить род кривой по формуле:

[math]\displaystyle{ g = \frac{1}{2}(d-1)(d-2) - \sum_P \delta_P, }[/math]

Другие важные инварианты: кратность m особенности (максимальное целое число, такое что все производные задающего кривую многочлена, порядок которых не превосходит m, равны нулю) и число Милнора.

См. также

• Категория Алгебраические кривые

Литература

• Ж.-П. Серр. Алгебраические группы и поля классов. — М.: Мир, 1968. — 285 с.
• Джон Милнор. Особые точки комплексных гиперповерхностей. — М.: Мир, 1971. — 121 с.
• Egbert Brieskorn, Horst Knörrer. Plane Algebraic Curves. — Birkhäuser, 1986.
• Hershel M. Farkas, Irwin Kra. Riemann Surfaces. — Springer, 1980.
• W. Fulton. Algebraic Curves: an introduction to algebraic geometry.
• C.G. Gibson. Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. — Cambridge University Press, 1998.
• специальные плоские кривые [1] Архивная копия от 21 июня 2018 на Wayback Machine (рус.)