Прямоугольная система координат

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует её широкому применению.

Связанные термины: декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям (названной так по имени Рене Декарта), а общей декартовой системой координат называют аффинную систему координат (не обязательно прямоугольную).

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Геометрия» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти^[1]. Декарт и Ферма применяли координатный метод только на плоскости. Французский священнослужитель Николай Орем использовал конструкции, подобные декартовым координатам, задолго до времён Декарта и Ферма^[2].

Развитие системы декартовых координат будет играть основную роль в развитии исчисления Исааком Ньютоном и Лейбницем^[3]. Двухкоординатное описание плоскости позднее было обобщено в понятие векторных пространств^[4].

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке. Использование ортов восходит, по-видимому, к Гамильтону и Максвеллу.

Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат [math]\displaystyle{ X'X }[/math] и [math]\displaystyle{ Y'Y }[/math]. Оси координат пересекаются в точке [math]\displaystyle{ O }[/math], которая называется началом координат, на каждой оси выбрано положительное направление.

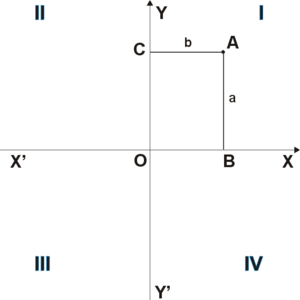
Положение точки [math]\displaystyle{ A }[/math] на плоскости определяется двумя координатами [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y }[/math]. Координата [math]\displaystyle{ x }[/math] равна длине отрезка [math]\displaystyle{ OB }[/math], координата [math]\displaystyle{ y }[/math] — длине отрезка [math]\displaystyle{ OC }[/math] в выбранных единицах измерения. Отрезки [math]\displaystyle{ OB }[/math] и [math]\displaystyle{ OC }[/math] определяются линиями, проведёнными из точки [math]\displaystyle{ A }[/math] параллельно осям [math]\displaystyle{ Y'Y }[/math] и [math]\displaystyle{ X'X }[/math] соответственно.

При этом координате [math]\displaystyle{ x }[/math] приписывается знак минус, если точка [math]\displaystyle{ B }[/math] лежит на луче [math]\displaystyle{ OX' }[/math] (а не на луче [math]\displaystyle{ OX }[/math], как на рисунке). Координате [math]\displaystyle{ y }[/math] приписывается знак минус, если точка [math]\displaystyle{ C }[/math] лежит на луче [math]\displaystyle{ OY' }[/math]. Таким образом,[math]\displaystyle{ OX' }[/math] и [math]\displaystyle{ OY' }[/math] являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Ось [math]\displaystyle{ X'X }[/math] называется осью абсцисс (лат. abscissus — букв. «отрезанный, отделённый»^[5]), а ось [math]\displaystyle{ Y'Y }[/math] — осью ординат (лат. ordinatus — букв. «упорядоченный, установленный в определённом порядке»^[5]). Координата [math]\displaystyle{ x }[/math] называется абсцисса точки [math]\displaystyle{ A }[/math], координата [math]\displaystyle{ y }[/math] — ордината точки [math]\displaystyle{ A }[/math].

Символически это записывают так:

[math]\displaystyle{ A(x,\;y) }[/math]

или

[math]\displaystyle{ A = (x,\;y) }[/math]

или указывают принадлежность координат конкретной точке с помощью индекса:

[math]\displaystyle{ x_A, x_B }[/math]

и т. д.

В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси [math]\displaystyle{ Y'Y }[/math] вверх, ось [math]\displaystyle{ X'X }[/math] смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).
Четыре угла (I, II, III, IV), образованные осями координат [math]\displaystyle{ X'X }[/math] и [math]\displaystyle{ Y'Y }[/math], называются координатными углами, четвертями или квадрантами <плоскости> (см. рис. 1).
- Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
- Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
- Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
- Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат [math]\displaystyle{ OX }[/math], [math]\displaystyle{ OY }[/math] и [math]\displaystyle{ OZ }[/math]. Оси координат пересекаются в точке [math]\displaystyle{ O }[/math], которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно^[6]) одинаковы для всех осей. [math]\displaystyle{ OX }[/math] — ось абсцисс, [math]\displaystyle{ OY }[/math] — ось ординат, [math]\displaystyle{ OZ }[/math] — ось аппликат.

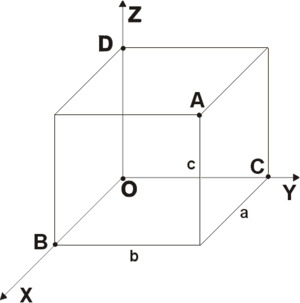
Положение точки [math]\displaystyle{ A }[/math] в пространстве определяется тремя координатами [math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math] и [math]\displaystyle{ z }[/math]. Координата [math]\displaystyle{ x }[/math] равна длине отрезка [math]\displaystyle{ OB }[/math], координата [math]\displaystyle{ y }[/math] — длине отрезка [math]\displaystyle{ OC }[/math], координата [math]\displaystyle{ z }[/math] — длине отрезка [math]\displaystyle{ OD }[/math] в выбранных единицах измерения. Отрезки [math]\displaystyle{ OB }[/math], [math]\displaystyle{ OC }[/math] и [math]\displaystyle{ OD }[/math] определяются плоскостями, проведёнными из точки [math]\displaystyle{ A }[/math] параллельно плоскостям [math]\displaystyle{ YOZ }[/math], [math]\displaystyle{ XOZ }[/math] и [math]\displaystyle{ XOY }[/math] соответственно.

Координата [math]\displaystyle{ x }[/math] называется абсциссой точки [math]\displaystyle{ A }[/math],

координата [math]\displaystyle{ y }[/math] — ординатой точки [math]\displaystyle{ A }[/math],

координата [math]\displaystyle{ z }[/math] — аппликата (лат. applicata — прилегающая)^[7] точки [math]\displaystyle{ A }[/math].

Символически это записывают так:

[math]\displaystyle{ A(x,\;y,\;z) }[/math]

или

[math]\displaystyle{ A = (x,\;y,\;z) }[/math]

или привязывают запись координат к конкретной точке с помощью индекса:

[math]\displaystyle{ x_A,\;y_A,\;z_A }[/math]

и т. п.

Каждая ось рассматривается как числовая прямая, то есть имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка [math]\displaystyle{ B }[/math] лежала не как на рисунке — на луче [math]\displaystyle{ OX }[/math], а на его продолжении в обратную сторону от точки [math]\displaystyle{ O }[/math] (на отрицательной части оси [math]\displaystyle{ OX }[/math]), то абсцисса [math]\displaystyle{ x }[/math] точки [math]\displaystyle{ A }[/math] была бы отрицательной (минус расстоянию [math]\displaystyle{ OB }[/math]). Аналогично и для двух других осей.

Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами^[8] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси [math]\displaystyle{ OX }[/math] против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси [math]\displaystyle{ OY }[/math], если этот поворот наблюдать со стороны положительного направления оси [math]\displaystyle{ OZ }[/math]).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.

Прямоугольная система координат в многомерном пространстве

Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать её [math]\displaystyle{ n }[/math]).

Для обозначения координат обычно^[9] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:

[math]\displaystyle{ x_1, x_2, x_3,\dots x_n. }[/math]

Для обозначения произвольной [math]\displaystyle{ i }[/math]-й координаты из этого набора используют буквенный индекс:

[math]\displaystyle{ x_i, }[/math]

а нередко обозначение [math]\displaystyle{ x_i, }[/math] используют и для обозначения всего набора, подразумевая, что индекс пробегает весь набор значений: [math]\displaystyle{ i = 1, 2, 3, \dots n }[/math].

В любой размерности пространства прямоугольные координатные системы делятся на два класса, правые и левые (или положительные и отрицательные). Для многомерных пространств какую-то одну из координатных систем произвольно (условно) называют правой, а остальные оказываются правыми или левыми в зависимости от того, той же они ориентации или нет^[10].

Обобщение понятий двумерного квадранта и трёхмерного октанта для [math]\displaystyle{ n }[/math]-мерного евклидова пространства — ортант или гипероктант.

Прямоугольные координаты вектора

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца^[11].

Таким образом, например, координаты [math]\displaystyle{ (x,y) }[/math] на рис.1 являются координатами вектора [math]\displaystyle{ \vec{OA} }[/math].

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.

В прямоугольных координатах очень просто записываются все операции над векторами:

Сложение и умножение на скаляр:

[math]\displaystyle{ \mathbf a + \mathbf b = (a_1 + b_1, a_2 + b_2, a_3 + b_3, \dots, a_n + b_n) }[/math]

или

[math]\displaystyle{ (\mathbf a + \mathbf b)_i = a_i + b_i, }[/math]

[math]\displaystyle{ c\ \mathbf a = (c\ a_1, c\ a_2, c\ a_3, \dots, c\ a_n) }[/math]

или

[math]\displaystyle{ (c\ \mathbf a)_i = c\ a_i. }[/math]

а отсюда и вычитание и деление на скаляр:

[math]\displaystyle{ \mathbf a - \mathbf b = (a_1 - b_1, a_2 - b_2, a_3 - b_3, \dots, a_n - b_n) }[/math]

или

[math]\displaystyle{ (\mathbf a - \mathbf b)_i = a_i - b_i, }[/math]

[math]\displaystyle{ \frac{\mathbf a}{\lambda} = \Big(\frac{a_1}{\lambda}, \frac{a_2}{\lambda}, \frac{a_3}{\lambda}, \dots, \frac{a_n}{\lambda}\Big) }[/math]

или

[math]\displaystyle{ \Big(\frac{\mathbf a}{\lambda}\Big)_i = \frac{a_i}{\lambda}. }[/math]

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

Скалярное произведение:

[math]\displaystyle{ \mathbf a \cdot \mathbf b = a_1 b_1 + a_2 b_2 + a_3 b_3 + \dots + a_n b_n }[/math]

или

[math]\displaystyle{ \mathbf a \cdot \mathbf b = \sum\limits_{i=1}^n a_i b_i, }[/math]

(Только в прямоугольных координатах с единичным масштабом по всем осям).

Через скалярное произведение можно вычислить длину вектора

[math]\displaystyle{ |\mathbf a| = \sqrt{\mathbf a\cdot\mathbf a} }[/math]

и угол между векторами

[math]\displaystyle{ \angle{(\mathbf a, \mathbf b)} = \mathrm{arccos}\frac{\mathbf a\cdot\mathbf b}{|\mathbf a|\cdot|\mathbf b|} }[/math]

Внешнее произведение:

[math]\displaystyle{ (\mathbf a \and \mathbf b)_{ij} = a_i b_j - a_j b_i }[/math]

для любой размерности пространства,

Векторное произведение (только для трехмерного же пространства, на котором оно и определено):

[math]\displaystyle{ (\mathbf a \times \mathbf b)_x = a_y b_z - a_z b_y }[/math]

[math]\displaystyle{ (\mathbf a \times \mathbf b)_y = a_z b_x - a_x b_z }[/math]

[math]\displaystyle{ (\mathbf a \times \mathbf b)_z = a_x b_y - a_y b_x }[/math]

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

Орты

Прямоугольная система координат^[12] (любой размерности) также описывается^[13] набором ортов (единичных векторов), сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты составляют базис, притом ортонормированный^[14].

В трёхмерном случае такие орты обычно обозначаются

[math]\displaystyle{ \mathbf{i} }[/math], [math]\displaystyle{ \mathbf{j} }[/math] и [math]\displaystyle{ \mathbf{k} }[/math]

или

[math]\displaystyle{ \mathbf{e}_x }[/math], [math]\displaystyle{ \mathbf{e}_y }[/math] и [math]\displaystyle{ \mathbf{e}_z }[/math].

Могут также применяться обозначения со стрелками ([math]\displaystyle{ \vec{i} }[/math], [math]\displaystyle{ \vec{j} }[/math] и [math]\displaystyle{ \vec{k} }[/math] или [math]\displaystyle{ \vec{e}_x }[/math], [math]\displaystyle{ \vec{e}_y }[/math] и [math]\displaystyle{ \vec{e}_z }[/math]) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

[math]\displaystyle{ [\mathbf{i}\,,\mathbf{j}]=\mathbf{k}; }[/math]
[math]\displaystyle{ [\mathbf{j}\,,\mathbf{k}]=\mathbf{i}; }[/math]
[math]\displaystyle{ [\mathbf{k}\,,\mathbf{i}]=\mathbf{j}. }[/math]

Для более высоких, чем 3, размерностей (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто^[15] это

[math]\displaystyle{ \mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3,\dots \mathbf{e}_n, }[/math]

где n — размерность пространства.

Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):

[math]\displaystyle{ \mathbf a = a_1\mathbf e_1 + a_2\mathbf e_2 + a_3\mathbf e_3 + \dots + a_n\mathbf e_n }[/math]

или

[math]\displaystyle{ \mathbf a = \sum\limits_{i=1}^n a_i\mathbf e_i, }[/math]

а для ортонормированного базиса координаты ещё и очень легко найти через скалярные произведения с ортами:

[math]\displaystyle{ a_i = \mathbf a \cdot \mathbf e_i. }[/math]

См. также

Примечания

↑ Bix, Robert A.; D'Souza, Harry J. Analytic geometry (неопр.). Encyclopædia Britannica. Дата обращения: 6 августа 2017. Архивировано 6 августа 2017 года.
↑ Kent, Alexander J. The Routledge Handbook of Mapping and Cartography : [англ.] / Alexander J. Kent, Peter Vujakovic. — Routledge, 2017-10-04. — ISBN 9781317568216. Архивная копия от 24 ноября 2021 на Wayback Machine
↑ A Tour of the Calculus, David Berlinski
↑ Axler, Sheldon. Linear Algebra Done Right - Springer. — 2015. — P. 1. — ISBN 978-3-319-11079-0. — doi:10.1007/978-3-319-11080-6.
↑ ^5,0 ^5,1 Словарь иностранных слов. — М.: Рус. яз., 1989. — 624 с. ISBN 5-200-00408-8
↑ Иногда это просто принципиально невозможно, если по осям откладываются величины разной физической размерности; впрочем, с геометрической точки зрения это замечание не слишком существенно, так как можно тогда считать масштабы по осям равными условно (например масштабы так, чтобы единицы совпадали при изображая на геометрической плоскости).
↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8
↑ Можно превратить правую координатную систему в левую и наоборот с помощью зеркального отражения.
↑ Но не обязательно: вопрос обозначений в конечном итоге определяется конкретным приложением.
↑ Это можно выяснить, исходя из того, можно ли какими-то вращениями (и переносами, если не совпадают начала координат) совместить данную координатную систему с той, ориентация которой правая по определению. Если да, то данная система считается правой, если нет, то левой. Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.
↑ Конец направленного отрезка — точка; прямоугольные координаты точки рассмотрены в статье выше.
↑ В этом параграфе будем подразумевать обычную декартову систему координат, то есть прямоугольную систему координат с одинаковым масштабом по всем осям; рассмотрение систем координат с разным масштабом по разным осям внесло бы здесь неоправданные формальные усложнения при довольно малом выигрыше содержательном отношении.
↑ Это описание очевидно полностью эквивалентно обычному заданию осей координат, надо только ещё задать начало координат (последнее нередко очевидно по умолчанию).
↑ При отказе от условия равномасштабности координатных осей — просто ортогональный базис.
↑ Впрочем, вместо буквы e нередко могут быть использованы и другие буквы. Как правило, это явно оговорено.

Ссылки

В. И. Гервидс. Модель декартовой системы координат (неопр.) (flash). НИЯУ МИФИ (10.03.2011). Дата обращения: 3 мая 2011.

[1] Bix, Robert A.; D'Souza, Harry J. Analytic geometry (неопр.). Encyclopædia Britannica. Дата обращения: 6 августа 2017. Архивировано 6 августа 2017 года.

[2] Kent, Alexander J. The Routledge Handbook of Mapping and Cartography : [англ.] / Alexander J. Kent, Peter Vujakovic. — Routledge, 2017-10-04. — ISBN 9781317568216. Архивная копия от 24 ноября 2021 на Wayback Machine

[3] A Tour of the Calculus, David Berlinski

[4] Axler, Sheldon. Linear Algebra Done Right - Springer. — 2015. — P. 1. — ISBN 978-3-319-11079-0. — doi:10.1007/978-3-319-11080-6.

[Словарь-5] 5,0 ^5,1 Словарь иностранных слов. — М.: Рус. яз., 1989. — 624 с. ISBN 5-200-00408-8

[6] Иногда это просто принципиально невозможно, если по осям откладываются величины разной физической размерности; впрочем, с геометрической точки зрения это замечание не слишком существенно, так как можно тогда считать масштабы по осям равными условно (например масштабы так, чтобы единицы совпадали при изображая на геометрической плоскости).

[7] Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8

[8] Можно превратить правую координатную систему в левую и наоборот с помощью зеркального отражения.

[9] Но не обязательно: вопрос обозначений в конечном итоге определяется конкретным приложением.

[10] Это можно выяснить, исходя из того, можно ли какими-то вращениями (и переносами, если не совпадают начала координат) совместить данную координатную систему с той, ориентация которой правая по определению. Если да, то данная система считается правой, если нет, то левой. Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.

[11] Конец направленного отрезка — точка; прямоугольные координаты точки рассмотрены в статье выше.

[12] В этом параграфе будем подразумевать обычную декартову систему координат, то есть прямоугольную систему координат с одинаковым масштабом по всем осям; рассмотрение систем координат с разным масштабом по разным осям внесло бы здесь неоправданные формальные усложнения при довольно малом выигрыше содержательном отношении.

[13] Это описание очевидно полностью эквивалентно обычному заданию осей координат, надо только ещё задать начало координат (последнее нередко очевидно по умолчанию).

[14] При отказе от условия равномасштабности координатных осей — просто ортогональный базис.

[15] Впрочем, вместо буквы e нередко могут быть использованы и другие буквы. Как правило, это явно оговорено.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Системы координат
Название координат	Абсцисса Ордината Аппликата
Типы систем координат	Прямолинейная система координат Криволинейная система координат
Двумерные координаты	Биангулярные координаты Бицентрические координаты Гиперболические координаты Полярные координаты Биполярные координаты Параболические координаты Эллиптические координаты Тетрациклические координаты Трилинейные координаты
Трёхмерные координаты	Цилиндрические координаты Сферические координаты Бисферические координаты Тороидальные координаты Цилиндрические параболические координаты Бицилиндрические координаты Эллипсоидальные координаты Конические координаты Пентасферические координаты Диполярная система координат
[math]\displaystyle{ n }[/math]-мерные координаты	Декартовы координаты Аффинные координаты Проективные координаты Плюккеровы координаты Барицентрические координаты
Физические координаты	Координаты Риндлера Координаты Борна Система небесных координат Географические координаты Главноортодромическая система координат
Связанные определения	Метод координат Начало координат Координатная ось Вектор Орт Система отсчёта Репер Коэффициенты Ламе Метрический тензор