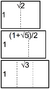
e (число)

Не следует путать с числами Эйлера I рода.

Не следует путать с постоянной Эйлера.

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π
Система счисления	Оценка числа [math]\displaystyle{ e }[/math]
Двоичная	10,101101111110000101010001011001…
Десятичная	2,7182818284590452353602874713527…
Шестнадцатеричная	2,B7E151628AED2A6A…
Шестидесятеричная	2; 43 05 48 52 29 48 35 …
Рациональные приближения	8/3; 11/4; 19/7; 87/32; 106/39; 193/71; 1264/465; 2721/1001; 23225/8544 (перечислено в порядке увеличения точности)
Непрерывная дробь	[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, …] (Эта непрерывная дробь не периодическая. Записана в линейной нотации)

2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354

---

Первые 1000 знаков после запятой числа e

(последовательность A001113 в OEIS)

Площадь области под графиком [math]\displaystyle{ y=\frac{1}{x} }[/math] на отрезке [math]\displaystyle{ 1 \leq x \leq e }[/math] равна 1

[math]\displaystyle{ e }[/math] — это такое число, для которого производная (тангенс угла наклона касательной) показательной функции f (x) = e^x (синяя кривая) в точке x = 0 равна 1 (касательная — красная линия). Для сравнения показаны функция f (x) = 2^x (пунктирная кривая) и f (x) = 4^x (штриховая кривая); производные которых не равны 1 при x = 0.

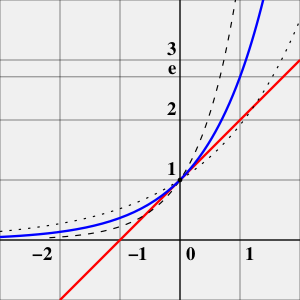
[math]\displaystyle{ e }[/math] — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда число [math]\displaystyle{ e }[/math] называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Максимум функции [math]\displaystyle{ x^{\frac{1}{x}} }[/math] достигается при [math]\displaystyle{ x=e }[/math].

Число [math]\displaystyle{ e }[/math] играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Поскольку функция экспоненты [math]\displaystyle{ e^x }[/math] интегрируется и дифференцируется «сама в себя», логарифмы именно по основанию [math]\displaystyle{ e }[/math] принимаются как натуральные.

Способы определения

Число [math]\displaystyle{ e }[/math] может быть определено несколькими способами.

• Через предел:

  [math]\displaystyle{ e = \lim_{x\to\infty} \left(1+\frac{1}{x}\right)^x }[/math] (второй замечательный предел).

  [math]\displaystyle{ e = \lim_{x\to 0}(1+x)^\frac{1}{x} }[/math]

  [math]\displaystyle{ e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}} }[/math] (это следует из формулы Муавра — Стирлинга).

• Как сумма ряда:

  [math]\displaystyle{ e = \sum_{n=0}^{\infty}{\frac{1}{n!}} }[/math] или [math]\displaystyle{ {\frac{1}{e}} = \sum_{n=2}^{\infty}{\frac{(-1)^{n}}{n!}} }[/math].

• Как единственное число [math]\displaystyle{ a }[/math], для которого выполняется

  [math]\displaystyle{ \int\limits_{1}^{a} \frac{dx}{x} = 1. }[/math]

• Как единственное положительное число [math]\displaystyle{ a }[/math], для которого верно

  [math]\displaystyle{ \frac d {dx} a^x = a^x. }[/math]

Свойства

• Производная экспоненты равна самой экспоненте:[math]\displaystyle{ \frac{de^x }{dx} = e^x. }[/math]
  Это свойство играет важную роль в решении дифференциальных уравнений. Так, например, общим решением дифференциального уравнения [math]\displaystyle{ \frac{df(x)}{dx} = f(x) }[/math] являются функции [math]\displaystyle{ f(x) = c e^x }[/math], где [math]\displaystyle{ c }[/math] — произвольная константа.
• Число [math]\displaystyle{ e }[/math] иррационально. Доказательство иррациональности является элементарным.

Доказательство иррациональности

Предположим, что [math]\displaystyle{ e }[/math] рационально. Тогда [math]\displaystyle{ e=p/q }[/math], где [math]\displaystyle{ p }[/math] — целое, а [math]\displaystyle{ q }[/math] — натуральное. Следовательно [math]\displaystyle{ p=eq }[/math] Умножая обе части уравнения на [math]\displaystyle{ (q-1)! }[/math], получаем [math]\displaystyle{ p(q-1)! = eq! = q!\sum_{n=0}^\infty{1\over n!} = \sum_{n=0}^\infty{q!\over n!} = \sum_{n=0}^q{q!\over n!}+\sum_{n=q+1}^\infty{q!\over n!} }[/math] Переносим [math]\displaystyle{ \sum_{n=0}^q{q!\over n!} }[/math] в левую часть: [math]\displaystyle{ \sum_{n=q+1}^\infty{q!\over n!} = p(q-1)! - \sum_{n=0}^q{q!\over n!} }[/math] Все слагаемые правой части целые, следовательно, и сумма в левой части — целая. Но эта сумма и положительна, значит, она не меньше 1. С другой стороны, [math]\displaystyle{ \sum_{n=q+1}^\infty{q!\over n!} = \sum_{m=1}^\infty{q!\over (q+m)!} = \sum_{m=1}^\infty{1\over (q+1)...(q+m)} \lt \sum_{m=1}^\infty{1\over (q+1)^m} }[/math] Суммируя геометрическую прогрессию в правой части, получаем: [math]\displaystyle{ \sum_{n=q+1}^\infty{q!\over n!} \lt {1\over q} }[/math] Поскольку [math]\displaystyle{ q\ge 1 }[/math], [math]\displaystyle{ \sum_{n=q+1}^\infty{q!\over n!} \lt 1 }[/math] Получаем противоречие.

• Число [math]\displaystyle{ e }[/math] трансцендентно. Впервые это было доказано в 1873 году Шарлем Эрмитом. Трансцендентность числа [math]\displaystyle{ e }[/math] следует из теоремы Линдемана.
• Предполагается, что [math]\displaystyle{ e }[/math] — нормальное число, то есть частота появления разных цифр в его записи одинакова. В настоящее время (2017) эта гипотеза не доказана.
• Число [math]\displaystyle{ e }[/math] является вычислимым (а значит, и арифметическим) числом.
• [math]\displaystyle{ e^{ix} = \cos(x) + i\cdot\sin(x) }[/math], см. формула Эйлера, в частности
  • [math]\displaystyle{ e^{i\pi} + 1 = 0. }[/math]
  • [math]\displaystyle{ e=\cos(i) - i \sin(i)=\sinh(1) + \cosh(1) }[/math]
• Формула, связывающая числа [math]\displaystyle{ e }[/math] и [math]\displaystyle{ \pi }[/math], т. н. интеграл Пуассона или интеграл Гаусса

  [math]\displaystyle{ \int\limits_{-\infty}^{\infty}\ e^{-x^2}{dx} = \sqrt{\pi} }[/math]

• Для любого комплексного числа z верны следующие равенства:

  [math]\displaystyle{ e^z=\sum_{n=0}^\infty \frac{1}{n!}z^n=\lim_{n\to\infty}\left(1+\frac{z}{n}\right)^n. }[/math]

• Число [math]\displaystyle{ e }[/math] разлагается в бесконечную цепную дробь следующим образом (простое доказательство этого разложения, связанное с аппроксимациями Паде, приведено в):

  [math]\displaystyle{ e = [2; \;1, 2, 1, \;1, 4, 1, \;1, 6, 1, \;1, 8, 1, \;1, 10, 1, \ldots] }[/math], то есть

  [math]\displaystyle{ e = 2+\cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{4 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{6 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{8 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{10 + \cfrac{1}{1 + \ldots}}}}}}}}}}}}}}} }[/math]

  или в эквивалентной записи:

  [math]\displaystyle{ e = 2+\cfrac{1}{1 + \cfrac{1}{2 + \cfrac{2}{3 + \cfrac{3}{4+\cfrac{4}{\ldots}}}}} }[/math]

• Для быстрого вычисления большого числа знаков удобнее использовать следующее разложение:

  [math]\displaystyle{ \frac{e+1}{e-1}=2 + \cfrac{1}{6 + \cfrac{1}{10 + \cfrac{1}{14 + \cfrac{1}{\ldots}}}} }[/math]

• [math]\displaystyle{ e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}}. }[/math]
• Представление Каталана:

  [math]\displaystyle{ e=2\cdot\sqrt{\frac{4}{3}}\cdot\sqrt[4]{\frac{6\cdot 8}{5\cdot 7}}\cdot\sqrt[8]{\frac{10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\cdot\sqrt[16]{\frac{18\cdot 20\cdot 22\cdot 24\cdot 26\cdot 28\cdot 30\cdot 32}{17\cdot 19\cdot 21\cdot 23\cdot 25\cdot 27\cdot 29\cdot 31}}\cdots }[/math]

• Представление через произведение:

  [math]\displaystyle{ e=\sqrt{3} \cdot \prod \limits_{k=1}^{\infty}\frac{\left ( 2k+3 \right )^{k+\frac 12}\left ( 2k-1 \right )^{k-\frac 12}}{\left (2k+1 \right )^{2k}} }[/math]

• Представление через числа Белла:

  [math]\displaystyle{ e = \frac{1}{B_n}\sum_{k=0}^\infty \frac{k^n}{k!} }[/math]

• Мера иррациональности числа [math]\displaystyle{ e }[/math] равна [math]\displaystyle{ 2 }[/math] (что есть наименьшее возможное значение для иррациональных чисел).

История

Данное число раньше иногда называли неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа [math]\displaystyle{ x }[/math] был равен [math]\displaystyle{ 10^7\cdot\,\log_{1/e}\left(\frac{x}{10^7}\right) }[/math].

Впервые константа негласно присутствует в приложении к переводу на английский язык (с латыни) вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует.

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Якоб Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма [math]\displaystyle{ \$1 }[/math] и начисляется [math]\displaystyle{ 100\% }[/math] годовых один раз в конце года, то итоговая сумма будет [math]\displaystyle{ \$2 }[/math]. Но если те же самые проценты начислять два раза в год, то [math]\displaystyle{ \$1 }[/math] умножается на [math]\displaystyle{ 1{,}5 }[/math] дважды, получая [math]\displaystyle{ \$1{,}00 \cdot 1{,}5^2 = \$2{,}25 }[/math]. Начисления процентов раз в квартал приводит к [math]\displaystyle{ \$1{,}00 \cdot 1{,}25^4 = \$2{,}44140625 }[/math], и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел: [math]\displaystyle{ \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n }[/math], и этот предел равен числу [math]\displaystyle{ e ~ (\approx 2{,}71828) }[/math].

[math]\displaystyle{ \$1{,}00 \cdot \left( 1+ \frac{1}{12} \right)^{12} = \$2{,}613035... }[/math]

[math]\displaystyle{ \$1{,}00 \cdot \left(1+\frac{1}{365}\right)^{365} = \$2{,}714567... }[/math]

Таким образом, константа [math]\displaystyle{ e }[/math] означает максимально возможную годовую прибыль при [math]\displaystyle{ 100\% }[/math] годовых и максимальной частоте капитализации процентов.

Первое известное использование этой константы, где она обозначалась буквой [math]\displaystyle{ b }[/math], встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.

Букву [math]\displaystyle{ e }[/math] начал использовать Эйлер в 1727 году, впервые она встречается в письме Эйлера немецкому математику Гольдбаху от 25 ноября 1731 года, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически», 1736 год. Соответственно, [math]\displaystyle{ e }[/math] обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву [math]\displaystyle{ c }[/math], буква [math]\displaystyle{ e }[/math] применялась чаще и в наши дни является стандартным обозначением.

В языках программирования символу [math]\displaystyle{ e }[/math] в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка FORTRAN для математических вычислений.

Мнемоника

• Число можно запомнить как 2, 7 и повторяющиеся 18, 28, 18, 28. Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов), после три первых простых числа (2, 3 и 5) и количество градусов в полном обороте (360).

Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: два и семь десятых, дважды Лев Толстой»

• Мнемоническое стихотворение, позволяющее запомнить первые 12 знаков после запятой (длины слов кодируют цифры числа e): Мы порхали и блистали, / Но застряли в перевале: / Не признали наши крали / Авторалли.^{[значимость факта?]}

Приближения

• [math]\displaystyle{ e \approx (1+\frac{1}{10^6})^{10^6} }[/math], с точностью 0,000001;

В соответствии с теорией непрерывных дробей наилучшими рациональными приближениями числа [math]\displaystyle{ e }[/math] будут подходящие дроби разложения числа [math]\displaystyle{ e }[/math] в непрерывную дробь.

Число 19/7 превосходит число [math]\displaystyle{ e }[/math] менее чем на 0,004;

Число 87/32 превосходит число [math]\displaystyle{ e }[/math] менее чем на 0,0005;

Число 193/71 превосходит число [math]\displaystyle{ e }[/math] менее чем на 0,00003;

Число 1264/465 превосходит число [math]\displaystyle{ e }[/math] менее чем на 0,000003;

Число 2721/1001 превосходит число [math]\displaystyle{ e }[/math] менее чем на 0,0000002;

• Площадь поверхности квадратной пирамиды, у которой боковые грани правильные треугольники с длиной ребра 1 (точность 0,014).^{[значимость факта?]}

Открытые проблемы

• Неизвестно, является ли число [math]\displaystyle{ e }[/math] элементом кольца периодов.
• Неизвестна мера иррациональности ни для одного из следующих чисел: [math]\displaystyle{ \pi + e, \pi - e, \pi \cdot e, \frac{\pi}{e}, \pi ^ e, e^{\pi^2}, e^e, 2^e. }[/math] Ни для одного из них неизвестно даже, является ли оно рациональным числом, алгебраическим иррациональным или трансцендентным числом. Следовательно, неизвестно, являются ли числа [math]\displaystyle{ \pi }[/math] и [math]\displaystyle{ e }[/math] алгебраически независимыми.
• Неизвестно, является ли первое число Скьюза [math]\displaystyle{ e^{e^{e^{79}}} }[/math] целым числом.

См. также

• Список объектов, названных в честь Леонарда Эйлера
• Математическая константа
• Число
• Пи (число)

Ссылки

• Число e — статья из энциклопедии «Кругосвет»
• Горобец Б. С. Мировые константы в основных законах физики и физиологии (рус.) // Наука и жизнь. — 2004. — № 2. (статья с примерами физического смысла констант [math]\displaystyle{ \pi }[/math] и [math]\displaystyle{ e }[/math])
• J. J. O'Connor, E. F. Robertson. История числа e (неопр.). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland (сентябрь 2001). (англ.)
• e for 2.71828… (англ.) (история и правило Джексона)
• «Экспонента и число е: просто и понятно Архивная копия от 25 сентября 2015 на Wayback Machine» — перевод статьи An Intuitive Guide To Exponential Functions & Number e | BetterExplained (англ.)
• Простое доказательство трансцендентности чисел e (на школьном уровне) и π см. стр. 520—535 Веберъ Г., Вельштейнъ И. Энциклопедiя элементарной математики. Том 1. Элементарная алгебра и анализъ. 1906