Постоянные Фейгенбаума

Основная статья: Теория бифуркаций

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π

Постоянные Фейгенбаума — универсальные постоянные, характеризующие бесконечный каскад бифуркаций удвоения периода при переходе к детерминированному хаосу (сценарий Фейгенбаума). Открыты Митчеллом Фейгенбаумом в 1975 году.

Каскад бифуркаций для логистического отображения. Над каждой точкой [math]\displaystyle{ a }[/math] на оси абсцисс отложены точки соответствующего предельного цикла отображения [math]\displaystyle{ x_{n+1} = ax_n(1 - x_n) }[/math]. Видно, что при увеличении [math]\displaystyle{ a }[/math] неподвижная точка сменяется циклом длины 2, он, в свою очередь, циклом длины 4, и так далее. Первая константа Фейгенбаума равна пределу отношения [math]\displaystyle{ L_i/L_{i+1} }[/math], где [math]\displaystyle{ L_i }[/math] — расстояния между точками бифуркаций.

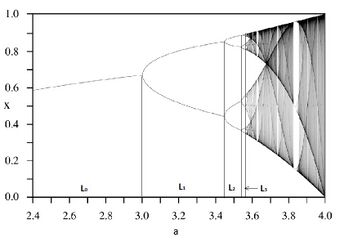
Первая константа Фейгенбаума

Одна из простейших динамических систем, где происходит каскад бифуркаций — это рекуррентные последовательности [math]\displaystyle{ x_{n+1} = f_a(x_n) }[/math], где [math]\displaystyle{ a }[/math] — некоторый параметр. Один из простейшиx примеров функции [math]\displaystyle{ f_a(x) }[/math] — логистическое отображение

[math]\displaystyle{ x_{n+1} = f_a(x_n) = ax_n(1 - x_n) }[/math]

В зависимости от параметра [math]\displaystyle{ a }[/math], в системе может присутствовать неподвижная точка или предельный цикл. При изменении [math]\displaystyle{ a }[/math] может произойти бифуркация, при которой предельный цикл удваивает свой период. Обозначим за [math]\displaystyle{ a_n }[/math] значения [math]\displaystyle{ a }[/math], при которых происходит удвоение периода. Оказывается, что при больших [math]\displaystyle{ n }[/math] значения [math]\displaystyle{ a_n }[/math] сходятся к фиксированному значению [math]\displaystyle{ a_\infty }[/math]. Сходимость происходит по геометрической прогрессии, причём показатель этой геометрической прогрессии оказывается одинаковым для широкого класса функций [math]\displaystyle{ f_a(x) }[/math] (универсальность Фейгенбаума). Этот показатель называется первой константой Фейгенбаума

[math]\displaystyle{ \delta = \lim_{n \to \infty} \frac{a_{n-1} - a_{n-2}}{a_n - a_{n-1}} = 4{,}669\;201\;609\;102\;990\;671\;853\;203\;820\;466\;\ldots, }[/math]

При [math]\displaystyle{ a \gt a_\infty }[/math] динамика системы становится хаотичной.

Физический смысл первой константы Фейгенбаума — скорость перехода к хаосу систем, испытывающих удвоение периода.

Она характеризует каскад удвоения периода во многих сложных динамических системах, таких, как система Рёсслера, турбулентность, рост популяций и пр.

Вторая константа Фейгенбаума

Вторая константа Фейгенбаума

[math]\displaystyle{ \alpha=2{,}502\;907\;875\;095\;892\;822\;283\;902\;873\;218\;\ldots }[/math] —

определяется как предел отношения между шириной ветвей на диаграмме бифуркаций (см. рисунок). Эта константа тоже возникает в описании многих динамических систем.

Свойства констант Фейгенбаума

Предполагается, что обе константы являются трансцендентными, хотя это ещё не доказано.

См. также

• Каскад бифуркаций
• Бифуркационная диаграмма
• Универсальность Фейгенбаума

Ссылки

• Д. И. Трубецков. Турбулентность и детерминированный хаос
• Feigenbaum Constant (англ.)

Примечания

привет