Натуральный логарифм

Функция натурального логарифма (синяя кривая) обратна к экспоненте (красная кривая)

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0

Натуральный логарифм — логарифм по основанию e, где [math]\displaystyle{ e }[/math] — трансцендентная константа, равная приблизительно [math]\displaystyle{ 2.718281828459 }[/math]. Он обозначается как [math]\displaystyle{ \ln x }[/math], [math]\displaystyle{ \log_ex }[/math] или иногда просто [math]\displaystyle{ \log x }[/math], если основание [math]\displaystyle{ e }[/math] подразумевается. Обычно число [math]\displaystyle{ x }[/math] под знаком логарифма вещественное, но можно расширить это понятие и на комплексные числа.

Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты [math]\displaystyle{ y=e^x }[/math], поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок справа). Как и экспонента, логарифмическая функция относится к категории трансцендентных функций.

Натуральные логарифмы полезны для решения алгебраических уравнений, в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, (например, нахождение сложных процентов).

Определение

Натуральный логарифм числа [math]\displaystyle{ a }[/math] — это показатель степени, в которую нужно возвести число e, чтобы получить [math]\displaystyle{ a }[/math]. Другими словами, натуральный логарифм [math]\displaystyle{ \ln a }[/math] есть решение [math]\displaystyle{ x }[/math] уравнения [math]\displaystyle{ e^x = a. }[/math]

Примеры:

[math]\displaystyle{ \ln e=1 }[/math], потому что [math]\displaystyle{ e^1=e }[/math];

[math]\displaystyle{ \ln 1=0 }[/math], потому что [math]\displaystyle{ e^0=1 }[/math].

Вещественный натуральный логарифм

[math]\displaystyle{ \ln a }[/math] определяется как площадь под кривой [math]\displaystyle{ f(x)=\frac{1}{x} }[/math] от [math]\displaystyle{ 1 }[/math] до [math]\displaystyle{ a }[/math].

Натуральный логарифм [math]\displaystyle{ \ln a }[/math] для вещественного числа [math]\displaystyle{ a }[/math] определён и однозначен для любого положительного числа [math]\displaystyle{ a. }[/math]

Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой [math]\displaystyle{ y=\frac{1}{x} }[/math] на промежутке [math]\displaystyle{ [1;a] }[/math]. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется данный логарифм, объясняет происхождение названия «натуральный».

Свойства

Из определения логарифма следует основное логарифмическое тождество:

[math]\displaystyle{ e^{\ln a} = a }[/math]

Приведём сводку формул в предположении, что все значения положительны:

	Формула	Пример
Произведение	[math]\displaystyle{ \ln(x y) = \ln x + \ln y }[/math]	[math]\displaystyle{ \ln (4\cdot 3) = \ln 4+ \ln 3 }[/math]
Частное	[math]\displaystyle{ \ln \left(\frac x y \right) = \ln x - \ln y }[/math]	[math]\displaystyle{ \ln \left(\frac{1}{e^2}\right) = \ln (1) - \ln (e^2) = 0 - 2 = -2 }[/math]
Степень	[math]\displaystyle{ \ln(x^p) = p \ln x }[/math]	[math]\displaystyle{ \ln (64) = \ln (2^6) = 6 \ln 2 }[/math]
Корень	[math]\displaystyle{ \ln \sqrt[p]{x} = \frac {\ln x} p }[/math]	[math]\displaystyle{ \ln \sqrt{10} = \frac{1}{2}\ln 10 }[/math]

Другие свойства:

• Из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений.
• С возрастанием аргумента возрастает и логарифм: если [math]\displaystyle{ 0\lt x\lt y, }[/math] то [math]\displaystyle{ \ln x \lt \ln y. }[/math]
• [math]\displaystyle{ \frac{h}{1+h} \leqslant \ln(1+h) \leqslant h, }[/math] если [math]\displaystyle{ h \gt -1. }[/math]

Связь с логарифмами по другому основанию

Логарифм может быть определён для любого положительного основания, отличного от [math]\displaystyle{ 1 }[/math], а не только для [math]\displaystyle{ e }[/math], но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем.

Логарифм [math]\displaystyle{ \log_a b }[/math] по основанию [math]\displaystyle{ a }[/math] можно преобразовать в натуральный логарифм и обратно:

[math]\displaystyle{ \ln b = \frac{\log_a b }{\log_a e} = \log_a b \cdot \ln a }[/math]

[math]\displaystyle{ \log_a b = \frac{\ln b }{\ln a} }[/math]

Связь десятичного ([math]\displaystyle{ \lg x }[/math]) и натурального логарифмов:

[math]\displaystyle{ \ln x \approx 2{,}30259\ \lg x; \quad \lg x \approx 0{,}43429\ \ln x }[/math]

Связь двоичного ([math]\displaystyle{ \operatorname{lb} x }[/math]) и натурального логарифмов:

[math]\displaystyle{ \ln x \approx 0,693147 \operatorname{lb} x; \quad \operatorname{lb} x \approx 1{,}442695 \ln x }[/math]

Логарифмическая функция

Графики логарифмических функций; красная кривая — натуральный логарифм

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию [math]\displaystyle{ y=\ln x }[/math]. Она определена при [math]\displaystyle{ x\gt 0 }[/math]. Область значений: [math]\displaystyle{ E(y)=(-\infty; + \infty) }[/math]. Эта кривая часто называется логарифмикой. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси [math]\displaystyle{ y }[/math]; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Функция является строго возрастающей, она непрерывна и неограниченно дифференцируема всюду в своей области определения.

Ось ординат ([math]\displaystyle{ x=0 }[/math]) является вертикальной асимптотой, поскольку:

[math]\displaystyle{ \lim_{x \to 0+} \ln x = - \infty }[/math]

Производная натуральной логарифмической функции равна:

[math]\displaystyle{ \frac {d} {dx} \ln x = \frac {1} {x} }[/math]

Простота этой формулы — одна из причин широкого использования именно натурального логарифма в анализе и при решении дифференциальных уравнений.

Натуральный логарифм равен площади под гиперболой

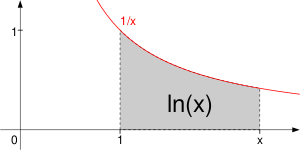
Проинтегрировав формулу для производной в интервале от [math]\displaystyle{ x=1 }[/math] до [math]\displaystyle{ x=b }[/math], мы получаем:

[math]\displaystyle{ \ln b = \int\limits_1^b {\frac {dx}{x}} }[/math]

Другими словами, натуральный логарифм [math]\displaystyle{ \ln{b} }[/math] равен площади под гиперболой [math]\displaystyle{ y=\frac {1}{x} }[/math] для указанного интервала [math]\displaystyle{ [1,b] }[/math].

С точки зрения общей алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения:

[math]\displaystyle{ f(xy)=f(x)+f(y) }[/math]

Аналитические свойства функции

Из формулы для производной натурального логарифма следует, что первообразная для гиперболы [math]\displaystyle{ y=1/x }[/math] имеет вид:

[math]\displaystyle{ \int { dx \over x} = \ln|x| + C, }[/math]

где [math]\displaystyle{ C }[/math] — произвольная константа интегрирования. Поскольку функция [math]\displaystyle{ y=1/x }[/math] состоит из двух ветвей (одна для положительных, другая для отрицательных [math]\displaystyle{ x }[/math]), семейство первообразных для [math]\displaystyle{ y=1/x }[/math] тоже состоит из двух подсемейств, причём константы интегрирования у них независимы одна от другой.

Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям:

[math]\displaystyle{ \int{\ln x\,\mathrm dx} = x\ln x-x+C }[/math]

В математическом анализе и теории дифференциальных уравнений большую роль играет понятие логарифмической производной функции [math]\displaystyle{ f(x) }[/math]:

[math]\displaystyle{ \frac{d}{dx} \ln(f(x)) = \frac{f'(x)}{f(x)} }[/math]

Методы вычисления логарифма

Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

[math]\displaystyle{ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots }[/math]

(Ряд 1)

Этот ряд, называемый «рядом Меркатора», сходится при [math]\displaystyle{ -1 \lt x \leqslant 1 }[/math]. В частности:

[math]\displaystyle{ \ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots }[/math]

Формула ряда 1 непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

[math]\displaystyle{ \ln \left(\frac{1+x}{1-x}\right)=2\left(x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\dots\right) }[/math]

(Ряд 2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа [math]\displaystyle{ z =\frac{1 + x}{1 - x} }[/math], ибо тогда [math]\displaystyle{ x = \frac{z - 1}{z + 1} }[/math] по абсолютной величине меньше единицы. Данный алгоритм уже пригоден для реальных численных расчётов значений логарифмов, однако не является наилучшим с точки зрения трудоёмкости.

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула::

[math]\displaystyle{ \ln x \approx \frac{\pi}{2 M(1,4/s)} - m \ln 2 }[/math]

где [math]\displaystyle{ M }[/math] обозначает арифметико-геометрическое среднее 1 и 4/s, и

[math]\displaystyle{ s = x \,2^m \gt 2^{p/2}, }[/math]

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Полезные пределы

Приведём несколько полезных пределов, связанных с логарифмами:

[math]\displaystyle{ \lim_{x \to 0} \frac{\ln (1+x)} {x} = 1 }[/math]

[math]\displaystyle{ \lim_{x \to 0+} x^b \ln x = 0 \quad (b \gt 0) }[/math]

[math]\displaystyle{ \lim_{x \to \infty} \frac{\ln x}{x^b} = 0 \quad (b \gt 0) }[/math]

[math]\displaystyle{ \ln x = \lim_{n \to \infty} n \left(\sqrt[n]x -1 \right) = \lim_{n \to \infty} n \left(1-\frac{1}{\sqrt[n]{x}}\right) }[/math]

[math]\displaystyle{ \ln x = \lim_{h \to 0} \frac{x^h-1}h }[/math]

Трансцендентность

Из теоремы Линдемана — Вейерштрасса (1885) вытекает следующее следствие: если аргумент [math]\displaystyle{ x }[/math] есть алгебраическое число, отличное от единицы, то значение [math]\displaystyle{ \ln x }[/math] есть не только иррациональное, но и трансцендентное число.

Непрерывные дроби

Хотя для представления логарифма отсутствуют классические непрерывные дроби, но можно использовать несколько «обобщённых непрерывных дробей», в том числе:

[math]\displaystyle{ \ln(1+x)=\frac{x^1}{1}-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}-\dots= \cfrac{x}{1-0\cdot x+\cfrac{1^2x}{2-1\cdot x+\cfrac{2^2x}{3-2x+\cfrac{3^2x}{4-3x+\cfrac{4^2x}{5-4x+\ddots}}}}} }[/math]

[math]\displaystyle{ \ln \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}} }[/math]

История

Основная статья: История логарифмов

Впервые натуральные логарифмы в современном понимании появились в 1619 году, когда лондонский учитель математики Джон Спейдель переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов. В 1649 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой [math]\displaystyle{ y=\frac {1}{x} }[/math] меняется по логарифмическому закону, и предложил называть этот вид логарифмов «гиперболическим».

Термин «натуральный логарифм» ввели в употребление Пьетро Менголи (1659 год) и Николас Меркатор в фундаментальном труде «Logarithmotechnia» (1668). Там же Меркатор описал разложение натурального логарифма в «ряд Меркатора».

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить [math]\displaystyle{ \log(-x) = \log(x) }[/math], в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.

Комплексные логарифмы

Основная статья: Комплексный логарифм

Комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всю комплексную плоскость (кроме нуля). В отличие от вещественного случая, функция комплексного логарифма многозначна.

Определение. Натуральный логарифм [math]\displaystyle{ \mathrm{Ln}\,z }[/math] комплексного числа [math]\displaystyle{ z }[/math] представляет собой решение [math]\displaystyle{ w }[/math] уравнения [math]\displaystyle{ e^w=z. }[/math]

Ненулевое число [math]\displaystyle{ z }[/math] можно представить в показательной форме:

[math]\displaystyle{ z=r \cdot e^{i (\varphi + 2 \pi k)}\;\;, }[/math] где [math]\displaystyle{ k }[/math] — произвольное целое число

Тогда [math]\displaystyle{ \mathrm{Ln}\,z }[/math] находится по формуле:

[math]\displaystyle{ \mathrm{Ln}\,z = \ln r + i \left( \varphi + 2 \pi k \right) }[/math]

Здесь [math]\displaystyle{ \ln\,r= \ln\,|z| }[/math] — вещественный логарифм. Отсюда вытекает:

Комплексный логарифм [math]\displaystyle{ \mathrm{Ln}\, z }[/math] существует для любого [math]\displaystyle{ z \ne 0 }[/math], и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное [math]\displaystyle{ 2\pi. }[/math]

Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале [math]\displaystyle{ (-\pi, \pi] }[/math]. Это значение называется главным значением комплексного натурального логарифма. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается [math]\displaystyle{ \ln\,z }[/math]. Если [math]\displaystyle{ z }[/math] — вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.

Логарифм отрицательного числа находится по формуле:

[math]\displaystyle{ \mathrm{Ln} (-x) = \ln x + i \pi (2 k + 1) \qquad (x\gt 0,\ k = 0, \pm 1, \pm 2 \dots) }[/math]

Примеры:

[math]\displaystyle{ \ln (1) = 0;\; \mathrm{Ln} (1) = 2k\pi i }[/math]

[math]\displaystyle{ \ln (-1) = i \pi;\; \mathrm{Ln} (-1) = (2k+1)i \pi }[/math]

[math]\displaystyle{ \ln (i) = i \frac{\pi} {2};\; \mathrm{Ln} (i) = i \frac{4k+1}{2} \pi }[/math]

Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:

[math]\displaystyle{ i\pi = \ln(-1) = \ln((-i)^2) = 2\ln(-i) = 2(-i\pi/2) = -i\pi }[/math] — явная ошибка.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ([math]\displaystyle{ k=-1 }[/math]). Причина ошибки — неосторожное использование свойства [math]\displaystyle{ \log_a{(b^p)} = p~\log_a b }[/math], которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.

• Функции натурального логарифма на комплексной плоскости (главная ветвь)
• 

  [math]\displaystyle{ z=Re(\ln(x+iy))| }[/math]

• 

  [math]\displaystyle{ z=Im(\ln(x+iy))| }[/math]

• 

  [math]\displaystyle{ z=|\ln(x+iy)| }[/math]

• 

  Суперпозиция трёх предыдущих графиков

Функция натурального логарифма комплексного числа может быть также определена как аналитическое продолжение вещественного логарифма на всю комплексную плоскость, кроме нуля. Пусть кривая [math]\displaystyle{ \Gamma }[/math] начинается в единице, заканчивается в z, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке [math]\displaystyle{ w }[/math] кривой [math]\displaystyle{ \Gamma }[/math] можно определить по формуле:

[math]\displaystyle{ \ln z = \int\limits_\Gamma {du \over u} }[/math]

Некоторые применения

Теория чисел

Распределение простых чисел асимптотически подчиняется простым законам:

1. Число простых чисел в интервале от 1 до [math]\displaystyle{ n }[/math] приблизительно равно [math]\displaystyle{ \frac{n}{\ln n} }[/math].
2. k-е простое число приблизительно равно [math]\displaystyle{ k \ln k }[/math].

Математический анализ

См. также: Список интегралов от логарифмических функций

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:

[math]\displaystyle{ \int {\operatorname{tg} x} \, dx = -\ln |\cos x| + C; \quad \int {\frac{dx}{\sqrt{x^2+a}}} = -\ln \ \left|\ x+\sqrt{x^2+a}\ \right| + C }[/math]

Теория вероятностей и статистика

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных.

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия.

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова.

Фракталы и размерность

Треугольник Серпинского (справа)

Логарифмы помогают выразить размерность Хаусдорфа для фрактала. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

[math]\displaystyle{ \frac {\ln 3}{\ln 2} \approx 1{,}58 }[/math]

Механика и физика

Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности.

Формула Циолковского применяется для расчёта скорости ракеты.

Химия и физическая химия

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Психология и физиология

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула — громкости звука, яркости света.

Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется.

Время на принятие решения при наличии выбора можно оценить по закону Хика.

Литература

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.

Ссылки

• "Разбираемся с натуральным логарифмом Архивная копия от 26 сентября 2013 на Wayback Machine" — перевод статьи Demystifying the Natural Logarithm (ln) | BetterExplained (англ.)