Формула Эйлера
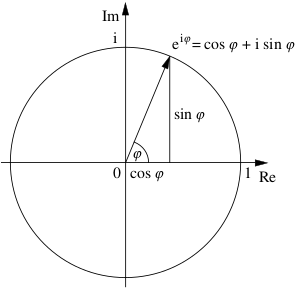
Формула Эйлера связывает комплексную экспоненту с тригонометрическими функциями. Названа в честь Леонарда Эйлера, который её ввёл.
Формула Эйлера утверждает, что для любого вещественного числа [math]\displaystyle{ x }[/math] выполнено следующее равенство:
- [math]\displaystyle{ e^{ix}=\cos x+i\sin x }[/math],
где [math]\displaystyle{ e }[/math] — одна из важнейших математических констант, определяющаяся следующей формулой: [math]\displaystyle{ e = \lim_{x\to\infty} \left(1+\frac{1}{x}\right)^x }[/math],
- [math]\displaystyle{ i }[/math] — мнимая единица.
История
Формула Эйлера впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году[1] и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum), которая была издана в 1722 году, уже после смерти автора[2]. Котс привёл её как небольшое предложение среди множества геометрических построений, которое после перевода на современный математический язык и исправления ошибки в знаке, имеет вид[3]:
- [math]\displaystyle{ \ln(\cos x+i\sin x)=i x }[/math].
Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748)[4], построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя у К. Весселя.
Производные формулы
При помощи формулы Эйлера можно определить функции [math]\displaystyle{ \sin }[/math] и [math]\displaystyle{ \cos }[/math] следующим образом:
- [math]\displaystyle{ \sin x=\frac{e^{ix}-e^{-ix}}{2i} }[/math],
- [math]\displaystyle{ \cos x=\frac{e^{ix}+e^{-ix}}{2} }[/math].
Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть [math]\displaystyle{ x=iy }[/math], тогда:
- [math]\displaystyle{ \sin iy=\frac{e^{-y}-e^y}{2i}=i\mathop{\mathrm{sh}}\,y }[/math],
- [math]\displaystyle{ \cos iy=\frac{e^{-y}+e^y}{2}=\mathop{\mathrm{ch}}\,y }[/math].
Известное тождество Эйлера, связывающее пять фундаментальных математических констант:
- [math]\displaystyle{ e^{i\pi}+1=0 }[/math]
является частным случаем формулы Эйлера при [math]\displaystyle{ x=\pi }[/math].
Применение в теории чисел
В аналитической теории чисел часто рассматриваются специальные суммы вида [math]\displaystyle{ \sum \limits_{x \in X} {e^{2 \pi i f(x)}} }[/math], где [math]\displaystyle{ X }[/math] — некоторое множество рассматриваемых объектов, а [math]\displaystyle{ f:\ X \to {\mathbb R} }[/math] — функция, отражающая изучаемые свойства объектов.
Для теории чисел, изучающей целые числа, имеют значение прежде всего выводимые из формулы Эйлера индикаторные тождества, касающиеся произвольного целого числа [math]\displaystyle{ n }[/math].
- [math]\displaystyle{ \sum \limits_{k=1}^{p} {e^{2 \pi \frac{nk}{p} i}} = p [p | n] = \left\{{ \begin{matrix} p, & n \equiv 0 \pmod p \\ 0, & n \not \equiv 0 \pmod p \end{matrix} }\right. }[/math]
- [math]\displaystyle{ \int \limits_{0}^{1} {e^{2 \pi n \alpha i}} = [n = 0] = \left\{{ \begin{matrix} 1, & n = 0 \\ 0, & n \not = 0 \end{matrix} }\right. }[/math]
Применение в комплексном анализе
Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: [math]\displaystyle{ x=a+ib=|x|(\cos\varphi+i\sin\varphi)=|x|e^{i\varphi} }[/math].
Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: [math]\displaystyle{ x=|x|e^{i\varphi} }[/math], [math]\displaystyle{ x^n=|x|^ne^{ni\varphi} }[/math]. Геометрический смысл данной формулы следующий: при возведении числа [math]\displaystyle{ x }[/math] в степень [math]\displaystyle{ n }[/math] его расстояние до центра возводится в степень [math]\displaystyle{ n }[/math], а угол поворота относительно оси [math]\displaystyle{ OX }[/math] увеличивается в [math]\displaystyle{ n }[/math] раз.
Формула возведения в степень верна не только для целых [math]\displaystyle{ n }[/math], но и для вещественных. В частности, показательная запись числа позволяет находить корни любой степени из любого комплексного числа.
Взаимосвязь с тригонометрией
Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
- [math]\displaystyle{ \cos x = \mathrm{Re}\left(e^{ix}\right) ={e^{ix} + e^{-ix} \over 2} }[/math]
- [math]\displaystyle{ \sin x = \mathrm{Im}\left(e^{ix}\right) ={e^{ix} - e^{-ix} \over 2i}. }[/math]
Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:
- [math]\displaystyle{ e^{ix} = \cos x + i \sin x \; }[/math]
- [math]\displaystyle{ e^{-ix} = \cos(- x) + i \sin(- x) = \cos x - i \sin x \; }[/math]
с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:
- [math]\displaystyle{ \cos(iy) = {e^{-y} + e^{y} \over 2} = \cosh(y) }[/math]
- [math]\displaystyle{ \sin(iy) = {e^{-y} - e^{y} \over 2i} = -{1 \over i} {e^{y} - e^{-y} \over 2} = i\sinh(y). }[/math]
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Например:
- [math]\displaystyle{ \begin{align} \cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\ & = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\ & = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right]. \end{align} }[/math]
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:
- [math]\displaystyle{ \begin{align} \cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \} = \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\ & = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\ & = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\ & = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x]. \end{align} }[/math]
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).
Доказательство
Доказательство формулы Эйлера можно провести с использованием ряда Маклорена. Разложим функцию [math]\displaystyle{ e^{ix} }[/math] в ряд Тейлора в окрестности точки a = 0 (в ряд Маклорена) по степеням [math]\displaystyle{ x }[/math]. Получим:
[math]\displaystyle{ e^{ix} = 1 + \frac{ix}{1!} + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \ldots=\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\ldots\right) + i\left(\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\ldots\right) }[/math]
Но
[math]\displaystyle{ 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\ldots=\cos x }[/math]
[math]\displaystyle{ \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\ldots=\sin x }[/math]
Поэтому [math]\displaystyle{ e^{ix}=\cos x + i\sin x }[/math], что и требовалось доказать.
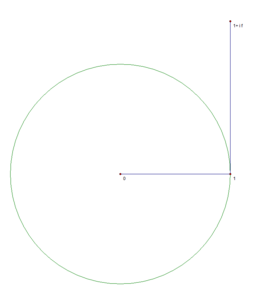
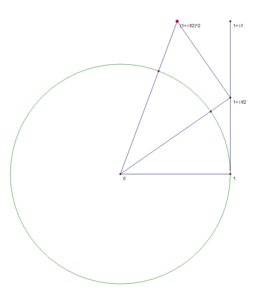
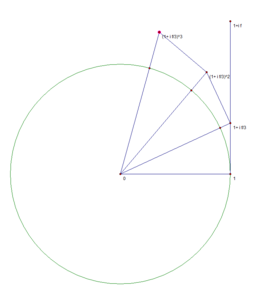
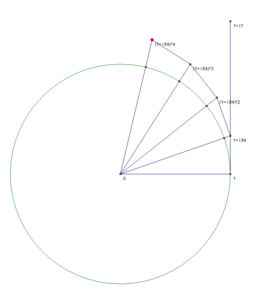
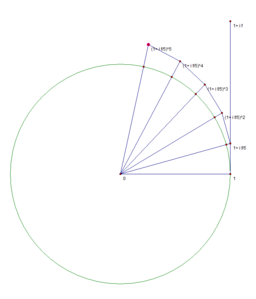
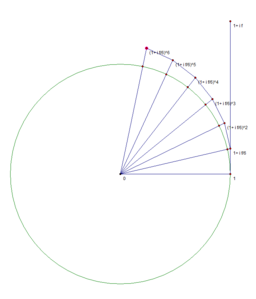
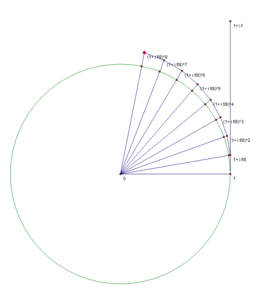
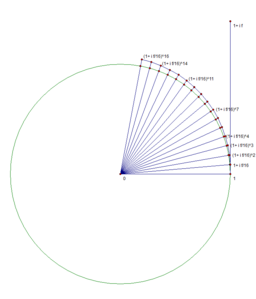
Наглядная демонстрация
Известно, что [math]\displaystyle{ e^x = \lim_{n\to\infty} \left(1+\frac{x}{n}\right)^n }[/math]. Нижеследующие изображения иллюстрируют, что предел [math]\displaystyle{ e^{i\varphi} = \lim_{n\to\infty} \left(1+\frac{i\varphi}{n}\right)^n }[/math] равен точке, находящейся на единичной окружности, и длина дуги от этой точки до точки 1 равняется [math]\displaystyle{ \varphi }[/math]. Это, в частности, связано с тем, что [math]\displaystyle{ \lim \limits_{x \to 0} {\frac{\sin x}{x}} = 1 }[/math].
-
n=1
-
n=2
-
n=3
-
n=4
-
n=5
-
n=6
-
n=8
-
n=16
Процесс изменения [math]\displaystyle{ e^{\varphi i} }[/math] при изменении [math]\displaystyle{ \varphi }[/math] можно также наглядно продемонстрировать через производную. Общеизвестно, что [math]\displaystyle{ \left({e^x}\right)' = e^x }[/math] и [math]\displaystyle{ \left({e^{f(x)}}\right)' = f'(x) e^{f(x)} }[/math]. Этот же факт остаётся верным и для комплексного значения функции. Рассматривая функцию [math]\displaystyle{ f(\varphi) = e^{\varphi i} }[/math], получим [math]\displaystyle{ f'(\varphi) = i f(\varphi) }[/math]. Поскольку в геометрическом представлении комплексных чисел умножение на [math]\displaystyle{ i }[/math] аналогично повороту на 90 градусов, то графическое изображение функции [math]\displaystyle{ f(\varphi) = e^{\varphi i} }[/math] и её производной будет аналогично чертежу действия центростремительной силы, для которого известен физический смысл.
Показательная форма комплексного числа
Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.
Пусть комплексное число [math]\displaystyle{ z }[/math] в тригонометрической форме имеет вид [math]\displaystyle{ z = r(\cos\varphi+i\sin\varphi) }[/math] . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим:
- [math]\displaystyle{ z = re^{i\varphi} }[/math]
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь [math]\displaystyle{ r = |z| }[/math] , [math]\displaystyle{ \varphi = \arg z }[/math].
Примечания
- ↑ Cotes R. Logometria (англ.) // Philosophical Transactions of the Royal Society of London : journal. — 1714-1716. — Vol. 29. — P. 32. — doi:10.1098/rstl.1714.0002. Архивировано 6 июля 2017 года.
- ↑ Cotes R. Harmonia mensurarum (неопр.). — 1722. — С. 28. Архивная копия от 7 июня 2020 на Wayback Machine
- ↑ González-Velasco Enrique A. Journey through Mathematics: Creative Episodes in Its History (англ.). — 2011. — P. 182. Архивная копия от 19 октября 2014 на Wayback Machine
- ↑ Euler L. Cap.VIII. De quantitatibus transcendentibus ex Circulo ortis // Introductio in analysin infinitorum (неопр.). — 1748. — Т. 1. — С. 104.
Литература
- Гутов А. З. Аналог формулы Эйлера для обобщённых синуса и косинуса // Современные методы физико-математических наук. Труды международной конференции. Орёл, 2006. С. 35—37. Архивная копия от 25 сентября 2020 на Wayback Machine
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
- Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — 530 с. Архивная копия от 7 июня 2015 на Wayback Machine