Мнимая единица

Мни́мая едини́ца — комплексное число, квадрат которого равен [math]\displaystyle{ -1 }[/math]. В математике, физике мнимая единица обозначается латинской буквой [math]\displaystyle{ i }[/math] (в электротехнике: [math]\displaystyle{ j }[/math])[1][2].
Введение мнимой единицы позволяет расширить поле вещественных чисел до поля комплексных чисел. Одной из причин введения мнимой единицы является то, что не каждое полиномиальное уравнение [math]\displaystyle{ f(x)=0 }[/math] с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение [math]\displaystyle{ x^2 + 1 = 0 }[/math] не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — об этом говорит основная теорема алгебры. Существуют и другие области, в которых комплексные числа приносят большую пользу.
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: при наличии трёх вещественных корней для получения двух из них формула Кардано требовала извлечения квадратных корней из отрицательных чисел.
Вплоть до конца XIX века наряду с символом [math]\displaystyle{ i }[/math] использовалось обозначение [math]\displaystyle{ \sqrt{-1}, }[/math] однако современные источники предписывают во избежание ошибок под знаком радикала помещать только неотрицательные выражения[3][4]. Более того, помимо мнимой единицы, существует ещё одно комплексное число, квадрат которого равен [math]\displaystyle{ -1, }[/math] — число [math]\displaystyle{ -i, }[/math] в паре с которым мнимая единица составляет следующие свойства:
- числа i и −i являются одновременно противоположными и обратными: последнее верно потому, что произведение этих чисел равно 1;
- i и −i комплексно сопряжены, так что их сумма (ноль) и произведение (единица) вещественны одновременно (свойства сопряжённых чисел).
Термин «мнимая единица» может употребляться не только для комплексных чисел, но и для их обобщений.
Степени мнимой единицы
Степени [math]\displaystyle{ i }[/math] повторяются в цикле:
- [math]\displaystyle{ \ldots }[/math]
- [math]\displaystyle{ i^{-3} = i }[/math]
- [math]\displaystyle{ i^{-2} = -1 }[/math]
- [math]\displaystyle{ i^{-1} = -i }[/math]
- [math]\displaystyle{ i^0 = 1 }[/math]
- [math]\displaystyle{ i^1 = i }[/math]
- [math]\displaystyle{ i^2 = -1 }[/math]
- [math]\displaystyle{ i^3 = -i }[/math]
- [math]\displaystyle{ i^4 = 1 }[/math]
- [math]\displaystyle{ \ldots }[/math]
что может быть записано для любой степени в виде:
- [math]\displaystyle{ i^{4n} = 1 }[/math]
- [math]\displaystyle{ i^{4n+1} = i }[/math]
- [math]\displaystyle{ i^{4n+2} = -1 }[/math]
- [math]\displaystyle{ i^{4n+3} = -i }[/math]
где n — любое целое число.
Отсюда: [math]\displaystyle{ i^n = i^{n \bmod 4} }[/math], где mod 4 — это остаток от деления на 4.
Возведение в комплексную степень является многозначной функцией. Например, таковой является величина [math]\displaystyle{ i^i }[/math], которая представляет бесконечное множество вещественных чисел ([math]\displaystyle{ i^i \subset \R }[/math]):
- [math]\displaystyle{ i^i = e^{-\left(\frac{\pi}2 + 2\pi k\right)}, }[/math] где [math]\displaystyle{ k\in\Z. }[/math]
При [math]\displaystyle{ k = 0 }[/math] получаем число [math]\displaystyle{ e^{-\frac{\pi}2} = 0{,}20787957635..., }[/math] соответствующее главному значению аргумента (или главному значению комплексного натурального логарифма) мнимой единицы.
- Представим основание в виде комплексной экспоненты (в этом случае её показателем будет комплексный логарифм):
- [math]\displaystyle{ z = i^i = \left ( e^{\operatorname{Ln} i} \right )^i = \left ( e^{\ln |i| + i \operatorname{Arg} i } \right )^i }[/math]
Альтернативным путем является представление основания в показательной форме:
- [math]\displaystyle{ z = i^i = \left ( |i| e^{i \operatorname{Arg} i } \right )^i }[/math]
Нетрудно убедиться, что оба полученных выражения тождественно равны.
Найдем модуль и аргумент числа [math]\displaystyle{ i }[/math]:
- [math]\displaystyle{ i = 0 + 1i = x + yi \quad \Rightarrow \quad x = 0, y = 1 }[/math]
- [math]\displaystyle{ |i| = \sqrt{x^2 + y^2} = \sqrt{0^2 + 1^2} = 1 }[/math]
- [math]\displaystyle{ \operatorname{Arg} i = \varphi + 2 \pi k }[/math], где [math]\displaystyle{ k \in \Z }[/math]
- [math]\displaystyle{ \varphi = \lim_{x \to +0} \left ( \operatorname{arctg} \frac{y}{x} \right ) = \lim_{x \to +0} \left ( \operatorname{arctg} \frac{1}{x} \right ) = \left [{ \color{white} \vdots } \operatorname{arctg} (+\infty) { \color{white} \vdots } \right ] = \frac{\pi}{2} }[/math]
- [math]\displaystyle{ \operatorname{Arg} i = \frac{\pi}{2} + 2 \pi k }[/math]
Подставим полученные значения для модуля и аргумента в выражение для [math]\displaystyle{ z }[/math]:
- [math]\displaystyle{ z = \left ( e^{\ln 1 + i \left( \frac{\pi}{2} + 2 \pi k \right ) } \right )^i = \left ( e^{i \left( \frac{\pi}{2} + 2 \pi k \right ) } \right )^i = e^{i^2 \left( \frac{\pi}{2} + 2 \pi k \right ) } = e^{- \left( \frac{\pi}{2} + 2 \pi k \right ) } }[/math]
Таким образом, получаем:
- [math]\displaystyle{ i^i = e^{- \left( \frac{\pi}{2} + 2 \pi k \right )} }[/math], где [math]\displaystyle{ k \in \Z }[/math] ∎
И очевидно, что:
- [math]\displaystyle{ i^i \subset \R }[/math]
- Теперь докажем, что число [math]\displaystyle{ e^{-\frac{\pi}{2}} }[/math] является частным значением [math]\displaystyle{ i^i }[/math], которое соответствует главному значению аргумента (или главному значению комплексного натурального логарифма) мнимой единицы.
Ранее было найдено главное значение аргумента мнимой единицы (т.е. такое, что попадает в промежуток [math]\displaystyle{ (-\pi, \pi] }[/math]):
- [math]\displaystyle{ \varphi = \frac{\pi}{2} \in (-\pi, \pi] }[/math]
Подставляя его вместо [math]\displaystyle{ \operatorname{Arg} i }[/math] в выражение для [math]\displaystyle{ z }[/math], получим искомое частное значение:
- [math]\displaystyle{ e^{-\varphi} = e^{-\frac{\pi}{2}} = 0{,}20787957635\ldots }[/math] ∎
Также верно, что [math]\displaystyle{ (-i)^{(-i)}=i^i }[/math].
Факториал
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- [math]\displaystyle{ i! = \Gamma(1+i) \approx 0.4980 - 0.1549i. }[/math]
Также
- [math]\displaystyle{ |i!| = \sqrt{\pi \over \sinh(\pi)} \approx 0.521564..., }[/math][5]
потому что |i!|2 = i! i! = i! (i)! = Γ(1 + i) Γ(1 − i), что по рекуррентному соотношению гамма-функции можно переписать как i Γ(i) Γ(1 − i), а затем по формуле дополнения Эйлера — как iπsin πi = πsinh π.
Корни из мнимой единицы

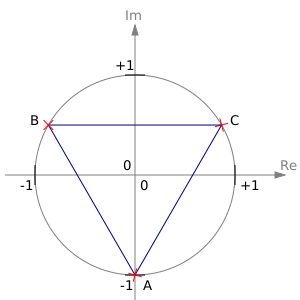
В поле комплексных чисел корень n-й степени имеет n значений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- [math]\displaystyle{ u_k=\cos {\frac{{\frac{\pi}{2}} + 2\pi k}{n}} +i\ \sin {\frac{{\frac{\pi}{2}} + 2\pi k}{n}}, \quad k=0,1,...,n-1 }[/math]
В частности, [math]\displaystyle{ \{\sqrt i\} = \left\{\frac{1+i}\sqrt2; ~\frac{-1-i}\sqrt2 \right\} }[/math] и [math]\displaystyle{ \{\sqrt[3]i\} = \left\{-i;~\frac{i+\sqrt3}2;~ \frac{i-\sqrt3}2\right\}. }[/math]
Также корни из мнимой единицы могут быть представлены в показательном виде:
- [math]\displaystyle{ u_k=e^{\frac{(\frac{\pi}{2} + 2\pi k) i}{n} }, \quad k=0,1,...,n-1. }[/math]
Иные мнимые единицы
В конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду «мнимых единиц расширения» может быть несколько. Но в этом случае могут возникать делители нуля и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения [math]\displaystyle{ x^2 = -1 }[/math].
К вопросу об интерпретации и названии
Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i.Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в.
Обозначения
Обычное обозначение — [math]\displaystyle{ i }[/math], но в электро- и радиотехнике мнимую единицу принято обозначать [math]\displaystyle{ j }[/math], чтобы не путать с обозначением мгновенной силы тока: [math]\displaystyle{ i = i (t) }[/math].
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как 𝕚.
См.также
Примечания
- ↑ Комплексное число // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Мнимая единица // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 708.
- ↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — С. 49. — 591 с.
- ↑ Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — 2-е изд. — М.: Наука, 1970. — С. 33. — 720 с.
- ↑ "abs(i!) Архивная копия от 6 июля 2015 на Wayback Machine", WolframAlpha.
Ссылки
- Мнимая единица // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.