Цепная дробь
Цепная дробь или непрерывная дробь (англ. contunued fraction) — это конечное или бесконечное математическое выражение вида
- [math]\displaystyle{ [a_0; a_1, a_2, a_3,\cdots] = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \ldots}}}, }[/math]
где все [math]\displaystyle{ a_i }[/math] — вещественные числа. Если [math]\displaystyle{ a_0 }[/math] — целое число, а все остальные [math]\displaystyle{ a_n }[/math] — натуральные числа (положительные целые), то такая цепная дробь называется регулярной[1], часто под цепной дробью понимается именно регулярная цепная дробь. Числа [math]\displaystyle{ a_0, a_1, a_2, a_3, \dots }[/math] называются неполными частными или элементами цепной дроби[2][3].
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально.
Цепные дроби позволяют находить наилучшие приближения вещественных чисел в виде обычных дробей (так называемые диофантовы приближения). Они широко используются в теории чисел и вычислительной математике, а их обобщения оказались чрезвычайно полезны в математическом анализе и других разделах математики. Используются также в физике, небесной механике, технике и других прикладных сферах деятельности.
Разложение в цепную дробь
Любое вещественное число [math]\displaystyle{ x }[/math] может быть представлено (конечной или бесконечной, периодической или непериодической) цепной дробью [math]\displaystyle{ [a_0; a_1, a_2, a_3,\ldots] }[/math], где
- [math]\displaystyle{ a_0 = \lfloor x \rfloor,\quad x_0 = x - a_0, }[/math]
- [math]\displaystyle{ a_1 = \left\lfloor \frac{1}{x_0} \right\rfloor,\quad x_1 = \frac{1}{x_0} - a_1, }[/math]
- [math]\displaystyle{ \dots }[/math]
- [math]\displaystyle{ a_n = \left\lfloor \frac{1}{x_{n-1}} \right\rfloor,\quad x_n = \frac{1}{x_{n-1}} - a_n, }[/math]
- [math]\displaystyle{ \dots }[/math]
где [math]\displaystyle{ \lfloor x \rfloor }[/math] обозначает целую часть числа [math]\displaystyle{ x }[/math].
Для рационального числа [math]\displaystyle{ x }[/math] это разложение оборвётся по достижении нулевого [math]\displaystyle{ x_n }[/math] для некоторого [math]\displaystyle{ n }[/math]. В этом случае [math]\displaystyle{ x }[/math] представляется конечной цепной дробью [math]\displaystyle{ x = [a_0; a_1, \ldots, a_n] }[/math]. Эффективным алгоритмом для преобразования обычной дроби в цепную является алгоритм Евклида. Представление рационального числа в виде непрерывной дроби неоднозначно: если приведённый здесь алгоритм даёт непрерывную дробь [math]\displaystyle{ [\dots, a_n] }[/math], то непрерывная дробь [math]\displaystyle{ [\dots, a_n-1, 1] }[/math] соответствует тому же самому числу.
Для иррационального [math]\displaystyle{ x }[/math] все величины [math]\displaystyle{ x_n }[/math] будут ненулевыми и процесс разложения можно продолжать бесконечно. В этом случае [math]\displaystyle{ x }[/math] представляется бесконечной цепной дробью [math]\displaystyle{ x = [a_0; a_1, a_2, a_3,\ldots] }[/math]. Если последовательность [math]\displaystyle{ [a_0; a_1, a_2, a_3,\ldots] }[/math] состоит из бесконечно повторяющегося набора одних и тех же чисел (периода), то цепная дробь называется периодической. Число представляется бесконечной периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью, то есть иррациональным корнем квадратного уравнения с целыми коэффициентами.
Подходящие дроби
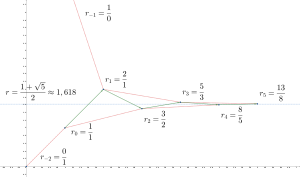
n-й («энной») подходящей дробью для цепной дроби [math]\displaystyle{ x = [a_0; a_1, a_2, a_3, \ldots] }[/math] называется конечная цепная дробь [math]\displaystyle{ [a_0; a_1, \ldots, a_n] }[/math], значение которой есть некоторое рациональное число [math]\displaystyle{ p_n/q_n }[/math]. Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен [math]\displaystyle{ x }[/math]. Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен [math]\displaystyle{ x }[/math]. Таким образом, значение цепной дроби всегда находится между значениями соседних подходящих дробей.
Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
- [math]\displaystyle{ p_{-1} = 1,\quad p_0 = a_0,\quad p_n = a_n p_{n-1} + p_{n-2}; }[/math]
- [math]\displaystyle{ q_{-1} = 0,\quad q_0 = 1,\quad q_n = a_n q_{n-1} + q_{n-2}. }[/math]
Таким образом, величины [math]\displaystyle{ p_n }[/math] и [math]\displaystyle{ q_n }[/math] являются полиномами от [math]\displaystyle{ a_0, a_1, \dots, a_n }[/math], называемыми континуантами:
- [math]\displaystyle{ p_n = K_{n+1}(a_0, a_1, \dots, a_n), }[/math]
- [math]\displaystyle{ q_n = K_n(a_1, a_2, \dots, a_n). }[/math]
Последовательности как числителей [math]\displaystyle{ \{p_n\} }[/math], так и знаменателей [math]\displaystyle{ \{q_n\} }[/math] подходящих дробей являются строго возрастающими.
Числители и знаменатели соседних подходящих дробей связаны соотношением
| [math]\displaystyle{ p_n q_{n-1} - q_n p_{n-1} = (-1)^{n-1}. }[/math] | (1) |
Подходящие дроби, как видно из этого соотношения, всегда несократимы. Перепишем соотношение в виде
- [math]\displaystyle{ \frac{p_n}{q_n} - \frac{p_{n-1}}{q_{n-1}} = \frac{(-1)^{n-1}}{q_{n-1} q_n}. }[/math]
Отсюда следует[4], что
- [math]\displaystyle{ \left|x - \frac{p_{n-1}}{q_{n-1}}\right| \lt \frac{1}{q_{n-1}q_n} \lt \frac{1}{q_{n-1}^2}. }[/math]
Приближение вещественных чисел рациональными
Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число [math]\displaystyle{ x }[/math] разложить в цепную дробь, то её подходящие дроби будут удовлетворять неравенству
- [math]\displaystyle{ \left|x - \frac{p_n}{q_n}\right| \lt \frac{1}{q_n^2}. }[/math]
Следствия[5]:
- Подходящая дробь [math]\displaystyle{ p_n/q_n }[/math] является наилучшим приближением исходного числа среди всех дробей, знаменатель которых не превосходит [math]\displaystyle{ q_n. }[/math]
- Мера иррациональности любого иррационального числа не меньше 2.
Примеры
Разложим число [math]\displaystyle{ \pi = 3{,}14159265\dots }[/math] в непрерывную дробь и подсчитаем его подходящие дроби:
- [math]\displaystyle{ 3,\ \frac{22}{7},\ \frac{333}{106},\ \frac{355}{113},\ \frac{103993}{33102},\ \dots }[/math]
Вторая подходящая дробь [math]\displaystyle{ 22/7 }[/math] — это известное архимедово приближение. Четвёртая подходящая дробь [math]\displaystyle{ 355/113 }[/math] была впервые получена в Древнем Китае.
Свойства золотого сечения
Ниже приведено разложение золотого сечения:
- [math]\displaystyle{ \Phi = [1; 1, 1, 1, \dots]. }[/math]
Интересный результат, который следует из того, что выражение непрерывной дроби для [math]\displaystyle{ \Phi }[/math] не использует чисел, больших 1, состоит в том, что [math]\displaystyle{ \Phi }[/math] является одним из самых «плохо» приближаемых чисел. Точнее, теорема Гурвица[6] утверждает, что любое действительное число [math]\displaystyle{ r }[/math] может быть приближено дробью [math]\displaystyle{ m/n }[/math] так, что
- [math]\displaystyle{ \left|r - \frac{m}{n}\right| \lt \frac{1}{n^2 \sqrt 5}. }[/math]
Хотя практически все действительные числа [math]\displaystyle{ r }[/math] имеют бесконечно много приближений [math]\displaystyle{ m/n }[/math], которые находятся на значительно меньшем расстоянии от [math]\displaystyle{ r }[/math], чем эта верхняя граница, приближения для [math]\displaystyle{ \Phi }[/math] (то есть чи́сла 5/3, 8/5, 13/8, 21/13 и т. д.) в пределе достигают этой границы[7], удерживая расстояние на почти точно [math]\displaystyle{ 1 / (n^2 \sqrt 5) }[/math] от [math]\displaystyle{ \Phi }[/math], тем самым никогда не создавая столь хорошие приближения как, к примеру, 355/113 для π. Можно показать, что этим свойством обладает любое действительное число вида [math]\displaystyle{ (a + b\Phi)/(c + d\Phi) }[/math], где [math]\displaystyle{ a, b, c }[/math] и [math]\displaystyle{ d }[/math] являются целыми числами, причём [math]\displaystyle{ ad - bc = \pm 1 }[/math]; а также, что все остальные действительные числа могут быть приближены намного лучше.
Свойства и примеры
- Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:
- [math]\displaystyle{ 9/4 = [2; 3, 1] = [2; 4]. }[/math]
- Теорема Лагранжа: Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.
- Например:
- [math]\displaystyle{ \sqrt{2} = [1; 2, 2, 2, 2, \dots], }[/math]
- [math]\displaystyle{ \sqrt{42} = [6; 2, 12, 2, 12, 2, 12 \dots], }[/math]
- золотое сечение [math]\displaystyle{ \Phi = [1; 1, 1, 1, \dots]. }[/math]
- Теорема Гаусса — Кузьмина: почти для всех (кроме множества меры нуль) вещественных чисел распределение элементов соответствующих им цепных дробей подчиняется статистике Гаусса — Кузьмина; в частности, существует среднее геометрическое всех элементов, и оно равно постоянной Хинчина.
- Теорема Маршалла Холла. Если в разложении числа [math]\displaystyle{ x }[/math] в непрерывную дробь, начиная со второго элемента не встречаются числа большие [math]\displaystyle{ n }[/math], то говорят, что число [math]\displaystyle{ x }[/math] относится к классу [math]\displaystyle{ F(n) }[/math]. Любое вещественное число может быть представлено в виде суммы двух чисел из класса [math]\displaystyle{ F(4) }[/math] и в виде произведения двух чисел из класса [math]\displaystyle{ F(4). }[/math][8] В дальнейшем было показано, что любое вещественное число может быть представлено в виде суммы трёх чисел из класса [math]\displaystyle{ F(3) }[/math] и в виде суммы четырёх чисел из класса [math]\displaystyle{ F(2) }[/math]. Количество требуемых слагаемых в этой теореме не может быть уменьшено — для представления некоторых чисел указанным образом меньшего количества слагаемых недостаточно[9][10].
Открытые проблемы
Предпринимались попытки найти закономерности в разложениях в непрерывную дробь кубических иррациональностей[11], а также других алгебраических чисел степени, большей 2, и трансцендентных чисел[12]. Для некоторых трансцендентных чисел можно найти простую закономерность. Например, основание натурального логарифма представимо в виде[13]
- [math]\displaystyle{ e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, \ldots, 1, 1, 2n - 2, 1, 1, 2n, \ldots], }[/math]
а тангенс угла в 1 радиан — в виде[14]
- [math]\displaystyle{ \operatorname{tg} 1 = [1; 1, 1, 3, 1, 5, 1, 7, \ldots, 1, 2n + 1, 1, 2n + 3, \ldots]. }[/math]
У числа [math]\displaystyle{ \pi }[/math] простой закономерности не видно[15]:
- [math]\displaystyle{ \pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, \dots] }[/math]
Однако для обобщённой непрерывной дроби (см. ниже раздел Вариации и обобщения) прослеживается ясная закономерность.
Неизвестно, ограничены ли сверху неполные частные разложения таких чисел, как [math]\displaystyle{ \sqrt[3]{2} }[/math] или [math]\displaystyle{ \pi }[/math][12][16].
Приложения цепных дробей
Теория календаря
При разработке солнечного календаря необходимо найти рациональное приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для дробной части этого числа:
- [math]\displaystyle{ \frac{1}{4};\ \frac{7}{29};\ \frac{8}{33};\ \frac{31}{128};\ \frac{132}{545} \cdots }[/math]
Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось, поскольку оно мало отличается от следующего, гораздо более точного. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет (в григорианском — за 3280 лет). Очень точный вариант с четвёртой дробью (31/128, ошибка в сутки накапливается только за 100000 лет[17]) пропагандировал немецкий астроном Иоганн фон Медлер (1864 год), однако большого интереса он не вызвал.
Теория музыки
В теории музыки при построении равномерно темперированного строя требуют, чтобы интервал октавы [math]\displaystyle{ 2:1 }[/math] делился на [math]\displaystyle{ n }[/math] равных частей, и при этом интервал из [math]\displaystyle{ m }[/math] таких частей был по возможности близок к интервалу квинты [math]\displaystyle{ 3:2 }[/math]. Эти требования приводят к задаче отыскания рационального приближения для [math]\displaystyle{ \log_2 1{,}5 \approx 0{,}585 }[/math]. Третья подходящая дробь [math]\displaystyle{ 3/5 }[/math] даёт равномерно темперированную пентатонику. Четвёртая подходящая дробь [math]\displaystyle{ 7/12 }[/math] приводит к классическому делению октавы на 12 равных полутонов[18].
Решение сравнений первой степени
Рассмотрим сравнение: [math]\displaystyle{ ax \equiv b \pmod m }[/math], где [math]\displaystyle{ a,\ b }[/math] известны, причём можно считать, что [math]\displaystyle{ a }[/math] взаимно просто с [math]\displaystyle{ m }[/math]. Надо найти [math]\displaystyle{ x }[/math].
Разложим [math]\displaystyle{ \frac{m}{a} }[/math] в непрерывную дробь. Она будет конечной, и последняя подходящая дробь [math]\displaystyle{ \frac{p_n}{q_n} = \frac{m}{a} }[/math]. Подставим в формулу (1):
- [math]\displaystyle{ m q_{n-1} - a p_{n-1} = (-1)^{n-1}. }[/math]
Отсюда вытекает:
- [math]\displaystyle{ a p_{n-1} \equiv (-1)^n \pmod m, }[/math]
или
- [math]\displaystyle{ \ a (-1)^n p_{n-1} \equiv 1 \pmod m. }[/math]
Вывод: класс вычетов [math]\displaystyle{ x \equiv (-1)^n p_{n-1} b \pmod m }[/math] является решением исходного сравнения.
Другие приложения
- Доказательство иррациональности чисел. Например, с помощью цепных дробей была доказана иррациональность значения дзета-функции Римана [math]\displaystyle{ \zeta(3) }[/math] (константа Апери)
- Решение в целых числах уравнения Пелля[19]: [math]\displaystyle{ \;x^2-n y^2=1\; }[/math] и других уравнений диофантова анализа
- Определение заведомо трансцендентного числа (см. теорема Лиувилля)
- Алгоритмы факторизации SQUFOF и CFRAC.
- Характеристика ортогональных многочленов
- Характеристика устойчивых многочленов
Вариации и обобщения
Ряд источников дают обобщённое определение непрерывной дроби, допуская для числителей в её звеньях не только 1, но и другие целые (в некоторых источниках допускаются даже комплексные) числа[2]:
- [math]\displaystyle{ [a_0; a_1, a_2, a_3, \dots] = a_0 + \cfrac{b_1}{a_1 + \cfrac{b_2}{a_2 + \cfrac{b_3}{a_3 + \ldots}}}. }[/math]
Это обобщение повышает гибкость теории, но имеет два недостатка: разложение вещественного числа в непрерывную дробь становится неоднозначным и, кроме того, существование предела подходящих дробей уже не гарантировано — предел может быть бесконечен или вообще отсутствовать.
Для обобщённых непрерывных дробей формулы Эйлера имеют вид[20]:
- [math]\displaystyle{ p_{-1} = 1,\quad p_0 = a_0,\quad p_n = a_n p_{n-1} + b_n p_{n-2}; }[/math]
- [math]\displaystyle{ q_{-1} = 0,\quad q_0 = 1,\quad q_n = a_n q_{n-1} + b_n q_{n-2}. }[/math]
При этом
- [math]\displaystyle{ p_n q_{n-1} - q_n p_{n-1} = (-1)^{n-1}b_1 b_2\dots b_n. }[/math]
Частный случай, в котором все [math]\displaystyle{ b_n = -1 }[/math], называется непрерывной дробью Хирцебруха[21].
Выше было сказано, что разложение числа [math]\displaystyle{ \pi }[/math] в классическую непрерывную дробь не содержит видимой закономерности. Для обобщённой же непрерывной дроби имеет место формула Браункера[22]:
- [math]\displaystyle{ \frac \pi 4 = \cfrac{1}{1 + \cfrac{1^2}{2 + \cfrac{3^2}{2 + \cfrac{5^2}{2 + \cfrac{7^2}{2 + \cfrac{9^2}{2 + \ddots}}}}}} }[/math]
Другое направление обобщения состоит в построении и применении аппарата непрерывных дробей не для чисел, а для многочленов — используется тот факт, что делимость многочленов по своим свойствам близка к делимости целых чисел[23]. Всякий многочлен или дробно-рациональная функция может быть разложена в непрерывную дробь[24]:
- [math]\displaystyle{ \cfrac{b_1}{a_1 + \cfrac{b_2 x}{a_2 + \cfrac{b_3 x}{a_3 + \ldots}}}. }[/math]
Пример: получим разложение для функции [math]\displaystyle{ f(x) = \frac{1 - x}{1 - 5x + 6x^2} }[/math]:
- [math]\displaystyle{ f(x) = \cfrac{1}{1 - \cfrac{4 x}{1 - \cfrac{2 x}{-4 + 6x}}}. }[/math]
Можно установить соответствие между непрерывными дробями и углами на решётках на плоскости. В связи с этим существуют различные варианты «многомерных непрерывных дробей»[1].
Историческая справка
Античные математики умели представлять отношения несоизмеримых величин в виде цепочки последовательных подходящих отношений, получая эту цепочку с помощью алгоритма Евклида. По-видимому, именно таким путём Архимед получил приближение [math]\displaystyle{ \sqrt{3} \approx \frac {1351}{780} }[/math] — это 12-я подходящая дробь для [math]\displaystyle{ \sqrt{3} }[/math] или одна треть от 4-й подходящей дроби для [math]\displaystyle{ \sqrt{27} }[/math].

В V веке индийский математик Ариабхата применял аналогичный «метод измельчения» для решения неопределённых уравнений первой и второй степени. С помощью этой же техники было, вероятно, получено известное приближение для числа [math]\displaystyle{ \pi }[/math] (355/113). В XVI веке Рафаэль Бомбелли извлекал с помощью цепных дробей квадратные корни (см. его алгоритм).
Начало современной теории цепных дробей положил в 1613 году Пьетро Антонио Катальди. Он отметил основное их свойство (положение между подходящими дробями) и ввёл обозначение, напоминающее современное. Позднее его теорию расширил Джон Валлис, который и предложил термин «непрерывная дробь». Эквивалентный термин «цепная дробь» появился в конце XVIII века.
Применялись эти дроби в первую очередь для рационального приближения вещественных чисел; например, Христиан Гюйгенс использовал их для проектирования зубчатых колёс своего планетария. Гюйгенс уже знал, что подходящие дроби всегда несократимы и что они представляют наилучшее рациональное приближение для исходного числа.
В XVIII веке теорию цепных дробей в общих чертах завершили Леонард Эйлер и Жозеф Луи Лагранж.
См. также
Примечания
- ↑ Перейти обратно: 1,0 1,1 Karpenkov, 2022.
- ↑ Перейти обратно: 2,0 2,1 Цепная дробь // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.
- ↑ Арнольд, 2000, с. 12.
- ↑ Виноградов, 1952, с. 18.
- ↑ Виноградов, 1952, с. 22, пункт 2.
- ↑ Hardy, G. H.; Wright, E. M. Theorem 193 // An Introduction to the Theory of Numbers (англ.). — Fifth. — Oxford, 1979.
- ↑ Дэвенпорт, 1965, с. 93—95.
- ↑ M. Hall, On the sum and product of continued fractions, Annals of Math. 48 (1947) 966—993.
- ↑ B. Diviš, On sums of continued fractions, Acta Arith. 22 (1973) 157—173.
- ↑ T. W. Cusick and R. A. Lee, Sums of sets of continued fractions, Proc. Amer. Math. Soc. 30 (1971) 241—246.
- ↑ Вычисления в алгебре и теории чисел, 1976, Х. М. Старк. Объяснение некоторых экзотических непрерывных дробей, найденных Бриллхартом, с. 155—156.
- ↑ Перейти обратно: 12,0 12,1 P. Shiu. Computation of continued fractions without input values. — 1995.
- ↑ последовательность A003417 в OEIS: разложение e в непрерывную дробь.
- ↑ последовательность A093178 в OEIS: разложение [math]\displaystyle{ \operatorname{tg}\,1 }[/math] в непрерывную дробь.
- ↑ последовательность A001203 в OEIS: разложение [math]\displaystyle{ \pi }[/math] в непрерывную дробь.
- ↑ последовательность A002945 в OEIS: разложение [math]\displaystyle{ \sqrt[3]{2} }[/math] в непрерывную дробь.
- ↑ На самом деле из-за постепенного замедления вращения Земли, и, соответственно, постепенного уменьшения числа суток в году, подобный календарь накопил бы фактическую ошибку в одни сутки уже через 4000 лет.
- ↑ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. — Популярные лекции по математике. — М.: Физматгиз, 1963. — С. 14—15. — 20 с.
- ↑ Бугаенко В. О. Уравнения Пелля Архивная копия от 8 июля 2011 на Wayback Machine, М.:МЦНМО, 2001. ISBN 5-900916-96-0.
- ↑ Основы вычислительной математики, 1963, с. 57.
- ↑ Е. Ю. Смирнов. Фризы и цепные дроби. МЦНМО (17 марта 2020). Дата обращения: 17 апреля 2020. Архивировано 21 апреля 2021 года.
- ↑ John Wallis, Arithmetica Infinitorum (Oxford, England: Leon Lichfield, 1656), page 182. Архивная копия от 24 апреля 2021 на Wayback Machine. Brouncker expressed, as a continued fraction, the ratio of the area of a circle to the area of the circumscribed square (i.e., 4/π). The continued fraction appears at the top of page 182 (roughly) as: ☐ = 1 1/2 9/2 25/2 49/2 81/2 &c, where the square denotes the ratio that is sought. (Note: On the preceding page, Wallis names Brouncker as: "Dom. Guliel. Vicecon, & Barone Brouncher" (Lord William Viscount and Baron Brouncker).)
- ↑ Хованский А. Н. Приложения цепных дробей и их обобщений к вопросам приближённого анализа (главы 1 и 2). — М.: Гостехиздат, 1956.
- ↑ Основы вычислительной математики, 1963, с. 70—73.
Литература
- Арнольд В. И. Цепные дроби. — М.: МЦНМО, 2000. — Т. 14. — 40 с. — (Библиотека «Математическое просвещение»).
- Бескин Н. М. Цепные дроби // Квант. — 1970. — Т. 1. — С. 16—26,62.
- Бескин Н. М. Бесконечные цепные дроби // Квант. — 1970. — Т. 8. — С. 10—20.
- Боднар Д. И. Ветвящиеся цепные дроби. — К.: Наука, 1986. — 174 с.
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966. — 384 с.
- Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — 180 с.
- Вычисления в алгебре и теории чисел / Пер. с англ. Э. Г. Белаги, под ред. Б. Б. Венкова и Д. К. Фаддеева. — М.: Мир, 1976. — (Математика. Новое в зарубежной науке).
- Гладковский С. Н. Анализ условно-периодических цепных дробей, ч. 1. — Незлобная, 2009. — 138 с.
- Демидович Б. П., Марон И. А. Основы вычислительной математики. — Изд. 2-е. — М.: Физматлит, 1963. — С. 53—73. — 660 с.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд.второе. — М.: Просвещение, 1965. — С. 253—254.
- Дэвенпорт Г. Высшая арифметика. Введение в теорию чисел. — М.: Наука, 1965.
- Сизый С. В. Лекции по теории чисел. — Екатеринбург: Уральский государственный университет им. А. М. Горького, 1999.
- Скоробогатько В. Я. Теория ветвящихся цепных дробей и её применение в вычислительной математике. — М.: Наука, 1983. — 312 с.
- Хинчин А. Я. Цепные дроби. — М.: ГИФМЛ, 1960.
- Хованский А. Н. Приложение цепных дробей и их обобщений к вопросам приближенного анализа. — М.: Гостехиздат, 1956. — 204 с.
- Brezinski C. History of continued fractions and Padé approximants. NY: Springer, 1980.
- Karpenkov O. Geometry of Continued Fractions. 2nd edition. — Springer, 2022. — ISBN 978-3-662-65277-0.