Цепная дробь
Цепная дробь или непрерывная дробь (англ. contunued fraction) — это конечное или бесконечное математическое выражение вида
где все
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально.
Цепные дроби позволяют находить наилучшие приближения вещественных чисел в виде обычных дробей (так называемые диофантовы приближения). Они широко используются в теории чисел и вычислительной математике, а их обобщения оказались чрезвычайно полезны в математическом анализе и других разделах математики. Используются также в физике, небесной механике, технике и других прикладных сферах деятельности.
Разложение в цепную дробь
Любое вещественное число
где
Для рационального числа
Для иррационального
Подходящие дроби
n-й («энной») подходящей дробью для цепной дроби
Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:
Таким образом, величины
Последовательности как числителей
Числители и знаменатели соседних подходящих дробей связаны соотношением
| (1) |
Подходящие дроби, как видно из этого соотношения, всегда несократимы. Перепишем соотношение в виде
Отсюда следует[4], что
Приближение вещественных чисел рациональными
Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число
Следствия[5]:
- Подходящая дробь
- Мера иррациональности любого иррационального числа не меньше 2.
Примеры
Разложим число
Вторая подходящая дробь
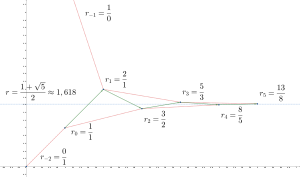
Свойства золотого сечения
Ниже приведено разложение золотого сечения:
Интересный результат, который следует из того, что выражение непрерывной дроби для
Хотя практически все действительные числа
Свойства и примеры
- Любое рациональное число может быть представлено в виде конечной цепной дроби двумя способами, например:
- Теорема Лагранжа: Число представляется в виде бесконечной периодической цепной дроби тогда и только тогда, когда оно является иррациональным решением квадратного уравнения с целыми коэффициентами.
- Например:
- Теорема Гаусса — Кузьмина: почти для всех (кроме множества меры нуль) вещественных чисел распределение элементов соответствующих им цепных дробей подчиняется статистике Гаусса — Кузьмина; в частности, существует среднее геометрическое всех элементов, и оно равно постоянной Хинчина.
- Теорема Маршалла Холла. Если в разложении числа
Открытые проблемы
Предпринимались попытки найти закономерности в разложениях в непрерывную дробь кубических иррациональностей[11], а также других алгебраических чисел степени, большей 2, и трансцендентных чисел[12]. Для некоторых трансцендентных чисел можно найти простую закономерность. Например, основание натурального логарифма представимо в виде[13]
а тангенс угла в 1 радиан — в виде[14]
У числа
Однако для обобщённой непрерывной дроби (см. ниже раздел Вариации и обобщения) прослеживается ясная закономерность.
Неизвестно, ограничены ли сверху неполные частные разложения таких чисел, как
Приложения цепных дробей
Теория календаря
При разработке солнечного календаря необходимо найти рациональное приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для дробной части этого числа:
Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось, поскольку оно мало отличается от следующего, гораздо более точного. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет (в григорианском — за 3280 лет). Очень точный вариант с четвёртой дробью (31/128, ошибка в сутки накапливается только за 100000 лет[17]) пропагандировал немецкий астроном Иоганн фон Медлер (1864 год), однако большого интереса он не вызвал.
Теория музыки
В теории музыки при построении равномерно темперированного строя требуют, чтобы интервал октавы
Решение сравнений первой степени
Рассмотрим сравнение:
Разложим
Отсюда вытекает:
или
Вывод: класс вычетов
Другие приложения
- Доказательство иррациональности чисел. Например, с помощью цепных дробей была доказана иррациональность значения дзета-функции Римана
- Решение в целых числах уравнения Пелля[19]:
- Определение заведомо трансцендентного числа (см. теорема Лиувилля)
- Алгоритмы факторизации SQUFOF и CFRAC.
- Характеристика ортогональных многочленов
- Характеристика устойчивых многочленов
Вариации и обобщения
Ряд источников дают обобщённое определение непрерывной дроби, допуская для числителей в её звеньях не только 1, но и другие целые (в некоторых источниках допускаются даже комплексные) числа[2]:
Это обобщение повышает гибкость теории, но имеет два недостатка: разложение вещественного числа в непрерывную дробь становится неоднозначным и, кроме того, существование предела подходящих дробей уже не гарантировано — предел может быть бесконечен или вообще отсутствовать.
Для обобщённых непрерывных дробей формулы Эйлера имеют вид[20]:
При этом
Частный случай, в котором все
Выше было сказано, что разложение числа
Другое направление обобщения состоит в построении и применении аппарата непрерывных дробей не для чисел, а для многочленов — используется тот факт, что делимость многочленов по своим свойствам близка к делимости целых чисел[23]. Всякий многочлен или дробно-рациональная функция может быть разложена в непрерывную дробь[24]:
Пример: получим разложение для функции
Можно установить соответствие между непрерывными дробями и углами на решётках на плоскости. В связи с этим существуют различные варианты «многомерных непрерывных дробей»[1].
Историческая справка
Античные математики умели представлять отношения несоизмеримых величин в виде цепочки последовательных подходящих отношений, получая эту цепочку с помощью алгоритма Евклида. По-видимому, именно таким путём Архимед получил приближение

В V веке индийский математик Ариабхата применял аналогичный «метод измельчения» для решения неопределённых уравнений первой и второй степени. С помощью этой же техники было, вероятно, получено известное приближение для числа
Начало современной теории цепных дробей положил в 1613 году Пьетро Антонио Катальди. Он отметил основное их свойство (положение между подходящими дробями) и ввёл обозначение, напоминающее современное. Позднее его теорию расширил Джон Валлис, который и предложил термин «непрерывная дробь». Эквивалентный термин «цепная дробь» появился в конце XVIII века.
Применялись эти дроби в первую очередь для рационального приближения вещественных чисел; например, Христиан Гюйгенс использовал их для проектирования зубчатых колёс своего планетария. Гюйгенс уже знал, что подходящие дроби всегда несократимы и что они представляют наилучшее рациональное приближение для исходного числа.
В XVIII веке теорию цепных дробей в общих чертах завершили Леонард Эйлер и Жозеф Луи Лагранж.
См. также
Примечания
- ↑ Перейти обратно: 1,0 1,1 Karpenkov, 2022.
- ↑ Перейти обратно: 2,0 2,1 Цепная дробь // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.
- ↑ Арнольд, 2000, с. 12.
- ↑ Виноградов, 1952, с. 18.
- ↑ Виноградов, 1952, с. 22, пункт 2.
- ↑ Hardy, G. H.; Wright, E. M. Theorem 193 // An Introduction to the Theory of Numbers (англ.). — Fifth. — Oxford, 1979.
- ↑ Дэвенпорт, 1965, с. 93—95.
- ↑ M. Hall, On the sum and product of continued fractions, Annals of Math. 48 (1947) 966—993.
- ↑ B. Diviš, On sums of continued fractions, Acta Arith. 22 (1973) 157—173.
- ↑ T. W. Cusick and R. A. Lee, Sums of sets of continued fractions, Proc. Amer. Math. Soc. 30 (1971) 241—246.
- ↑ Вычисления в алгебре и теории чисел, 1976, Х. М. Старк. Объяснение некоторых экзотических непрерывных дробей, найденных Бриллхартом, с. 155—156.
- ↑ Перейти обратно: 12,0 12,1 P. Shiu. Computation of continued fractions without input values. — 1995.
- ↑ последовательность A003417 в OEIS: разложение e в непрерывную дробь.
- ↑ последовательность A093178 в OEIS: разложение
- ↑ последовательность A001203 в OEIS: разложение
- ↑ последовательность A002945 в OEIS: разложение
- ↑ На самом деле из-за постепенного замедления вращения Земли, и, соответственно, постепенного уменьшения числа суток в году, подобный календарь накопил бы фактическую ошибку в одни сутки уже через 4000 лет.
- ↑ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. — Популярные лекции по математике. — М.: Физматгиз, 1963. — С. 14—15. — 20 с.
- ↑ Бугаенко В. О. Уравнения Пелля Архивная копия от 8 июля 2011 на Wayback Machine, М.:МЦНМО, 2001. ISBN 5-900916-96-0.
- ↑ Основы вычислительной математики, 1963, с. 57.
- ↑ Е. Ю. Смирнов. Фризы и цепные дроби. МЦНМО (17 марта 2020). Дата обращения: 17 апреля 2020. Архивировано 21 апреля 2021 года.
- ↑ John Wallis, Arithmetica Infinitorum (Oxford, England: Leon Lichfield, 1656), page 182. Архивная копия от 24 апреля 2021 на Wayback Machine. Brouncker expressed, as a continued fraction, the ratio of the area of a circle to the area of the circumscribed square (i.e., 4/π). The continued fraction appears at the top of page 182 (roughly) as: ☐ = 1 1/2 9/2 25/2 49/2 81/2 &c, where the square denotes the ratio that is sought. (Note: On the preceding page, Wallis names Brouncker as: "Dom. Guliel. Vicecon, & Barone Brouncher" (Lord William Viscount and Baron Brouncker).)
- ↑ Хованский А. Н. Приложения цепных дробей и их обобщений к вопросам приближённого анализа (главы 1 и 2). — М.: Гостехиздат, 1956.
- ↑ Основы вычислительной математики, 1963, с. 70—73.
Литература
- Арнольд В. И. Цепные дроби. — М.: МЦНМО, 2000. — Т. 14. — 40 с. — (Библиотека «Математическое просвещение»).
- Бескин Н. М. Цепные дроби // Квант. — 1970. — Т. 1. — С. 16—26,62.
- Бескин Н. М. Бесконечные цепные дроби // Квант. — 1970. — Т. 8. — С. 10—20.
- Боднар Д. И. Ветвящиеся цепные дроби. — К.: Наука, 1986. — 174 с.
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966. — 384 с.
- Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — 180 с.
- Вычисления в алгебре и теории чисел / Пер. с англ. Э. Г. Белаги, под ред. Б. Б. Венкова и Д. К. Фаддеева. — М.: Мир, 1976. — (Математика. Новое в зарубежной науке).
- Гладковский С. Н. Анализ условно-периодических цепных дробей, ч. 1. — Незлобная, 2009. — 138 с.
- Демидович Б. П., Марон И. А. Основы вычислительной математики. — Изд. 2-е. — М.: Физматлит, 1963. — С. 53—73. — 660 с.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд.второе. — М.: Просвещение, 1965. — С. 253—254.
- Дэвенпорт Г. Высшая арифметика. Введение в теорию чисел. — М.: Наука, 1965.
- Сизый С. В. Лекции по теории чисел. — Екатеринбург: Уральский государственный университет им. А. М. Горького, 1999.
- Скоробогатько В. Я. Теория ветвящихся цепных дробей и её применение в вычислительной математике. — М.: Наука, 1983. — 312 с.
- Хинчин А. Я. Цепные дроби. — М.: ГИФМЛ, 1960.
- Хованский А. Н. Приложение цепных дробей и их обобщений к вопросам приближенного анализа. — М.: Гостехиздат, 1956. — 204 с.
- Brezinski C. History of continued fractions and Padé approximants. NY: Springer, 1980.
- Karpenkov O. Geometry of Continued Fractions. 2nd edition. — Springer, 2022. — ISBN 978-3-662-65277-0.