Фотон

Это золотая статья пантеона энциклопедии Руниверсалис, в одной из версий этой статьи выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «Фотоны»)
У этого термина существуют и другие значения, см. Фотон (значения).
Фотон ([math]\displaystyle{ \gamma, }[/math] иногда [math]\displaystyle{ \gamma^0, h\nu }[/math])
Излучённые фотоны в когерентном луче лазераИзлучённые фотоны в когерентном луче лазера
Состав Фундаментальная частица
Семья Бозон
Группа Калибровочный бозон
Участвует во взаимодействиях Гравитационное[1][2],
электромагнитное, слабое
Античастица [math]\displaystyle{ \gamma }[/math] (истинно нейтральная частица)
Кол-во типов 1
Масса

0 (теоретическое значение)

< 10−22 эВ/c2 (экспериментальный предел)[3][4]
Время жизни Стабилен
Теоретически обоснована М. Планк (1900);
А. Эйнштейн (1905—1917)
Обнаружена 1923 (окончательное подтверждение)
Квантовые числа
Электрический заряд 0 (<10−35 e)[5][6][7]
Цветной заряд 0
Барионное число 0
Лептонное число 0
B−L 0
Спин 1 ħ
Спиральность ±1
Магнитный момент 0
Внутренняя чётность Не определена
Зарядовая чётность -1
Кол-во спиновых состояний 2
Изотопический спин 0
Странность 0
Очарование 0
Прелесть 0
Истинность 0
Гиперзаряд 0

Фото́н (от др.-греч. φῶς, фос — свет) — фундаментальная частица, квант электромагнитного излучения (в узком смысле — света) в виде поперечных электромагнитных волн и переносчик электромагнитного взаимодействия. Это безмассовая частица, способная существовать, только двигаясь со скоростью света. Электрический заряд фотона равен нулю. Спин фотона равен 1, но как всякая безмассовая частица он имеет две независимые поляризации (спиновых состояния) с проекцией спина на направление движения (спиральностью) ±1. В физике фотоны обозначаются буквой γ.

Современная наука рассматривает фотон как фундаментальную элементарную частицу, не обладающую строением и размерами.

С точки зрения квантовой механики фотону как квантовой частице свойственен корпускулярно-волновой дуализм: он проявляет одновременно свойства частицы и волны.

Квантовая электродинамика, основанная на квантовой теории поля и Стандартной модели, описывает фотон как калибровочный бозон, обеспечивающий электромагнитное взаимодействие между частицами: виртуальные фотоны[8] являются квантами-переносчиками электромагнитного поля[9].

Фотон — самая распространённая по численности частица во Вселенной: на один нуклон приходится не менее 20 миллиардов фотонов[10].

История

МезонМезонБарионНуклонКваркЛептонЭлектронАдронАтомМолекулаФотонW- и Z-бозоныГлюонГравитонЭлектромагнитное взаимодействиеСлабое взаимодействиеСильное взаимодействиеГравитацияКвантовая электродинамикаКвантовая хромодинамикаКвантовая гравитацияЭлектрослабое взаимодействиеТеория великого объединенияТеория всегоЭлементарная частицаВеществоБозон Хиггса
Краткий обзор различных семейств элементарных и составных частиц и теории, описывающие их взаимодействия. Элементарные частицы слева — фермионы, справа — бозоны. (Термины — гиперссылки на статьи ВП)

Современная теория света основана на работах многих учёных. Квантовый характер излучения и поглощения энергии электромагнитного поля был постулирован М. Планком в 1900 году для объяснения свойств теплового излучения[11]. Термин «фотон» введён химиком Гилбертом Льюисом в 1926 году[12]. В 1905—1917 годах Альбертом Эйнштейном опубликован[13][14][15][16] ряд работ, посвящённых противоречиям между результатами экспериментов и классической волновой теорией света, в частности, фотоэффекту и способности вещества находиться в тепловом равновесии с электромагнитным излучением.

Предпринимались попытки объяснить квантовые свойства света полуклассическими моделями, в которых свет по-прежнему описывался уравнениями Максвелла без учёта квантования, а объектам, излучающим и поглощающим свет, приписывались квантовые свойства (см., например, теорию Бора). Несмотря на то, что полуклассические модели оказали влияние на развитие квантовой механики (о чём, в частности, свидетельствует то, что некоторые их положения и даже следствия явным образом входят в современные квантовые теории[17]), эксперименты подтвердили правоту Эйнштейна о квантовой природе света (см., например, фотоэффект). Квантование энергии электромагнитного излучения не является исключением. В квантовой теории значения многих физических величин являются дискретными (квантованными). Примерами таких величин являются угловой момент, спин и энергия связанных систем.

Введение понятия фотона способствовало созданию новых теорий и физических приборов, а также стимулировало развитие экспериментальной и теоретической базы квантовой механики. Например, были изобретены мазер, лазер, открыто явление конденсации Бозе — Эйнштейна, сформулирована квантовая теория поля и вероятностная интерпретация квантовой механики. В современной Стандартной модели физики элементарных частиц существование фотонов является следствием того, что физические законы инвариантны относительно локальной калибровочной симметрии в любой точке пространства-времени (см. более подробное описание ниже в разделе Фотон как калибровочный бозон). Этой же симметрией определяются внутренние свойства фотона, такие как электрический заряд, масса и спин.

Среди приложений концепции фотонов есть такие, как фотохимия[18], видеотехника, компьютерная томография, микроскопия высокого разрешения и измерение межмолекулярных расстояний. Фотоны также используются в качестве элементов квантовых компьютеров[19] и наукоёмких приборов для передачи данных (см. квантовая криптография).

История названия и обозначения

Фотон изначально был назван Альбертом Эйнштейном «световым квантом» (нем. das Lichtquant)[13]. Современное название, которое фотон получил от греческого слова φῶς («свет»), было введено в 1926 году химиком Гилбертом Н. Льюисом[20], опубликовавшим свою теорию[21], в которой фотоны считались «несоздаваемыми и неуничтожимыми». Хотя теория Льюиса не нашла своего подтверждения, находясь в противоречии с экспериментальными данными, новое название для квантов электромагнитного поля стало использоваться многими физиками.

В физике фотон обычно обозначается символом γ (греческая буква гамма). Это обозначение восходит к гамма-излучению, открытому в 1900 году и состоящему из достаточно высокоэнергетических фотонов. Открытие гамма-излучения, одного из трёх видов (α-, β- и γ-лучи) ионизирующей радиации, излучаемых известными на тот момент радиоактивными веществами, принадлежит Паулю Вилларду, электромагнитную природу гамма-лучей доказали в 1914 году Эрнест Резерфорд и Эдвард Андрейд. В химии и оптической инженерии для фотонов часто используют обозначение hν, где h — постоянная Планка и ν (греческая буква ню) — частота фотонов. Произведение этих двух величин есть энергия фотона.

История развития концепции фотона

Основная статья: Свет
Опыт Томаса Юнга по интерференции света на двух щелях (1805 год) показал, что свет может рассматриваться как волна. Этим опытом были опровергнуты ранние теории света как однородного и равномерного потока частиц

В большинстве теорий, разработанных до XVIII века, свет рассматривался как поток частиц. Одна из первых таких теорий была изложена в «Книге об оптике» Ибн ал-Хайсамом в 1021 году. В ней учёный представлял световой луч в виде потока мельчайших частиц, которые «испытывают нехватку всех заметных качеств, кроме энергии»[22]. Так как подобные модели не смогли объяснить такие явления как рефракция, дифракция и двойное лучепреломление, была предложена волновая теория света, основателями которой стали Рене Декарт (1637)[23], Роберт Гук (1665)[24], и Христиан Гюйгенс (1678)[25]. Однако модели, основанные на идее дискретного строения света, оставались преобладающими, во многом из-за влияния авторитета Исаака Ньютона, придерживавшегося этих теорий[26][27].

В начале XIX века Томас Юнг и Огюстен Френель наглядно показали в своих опытах явления интерференции и дифракции света, после чего примерно к 1850 году волновые модели стали общепринятыми[28]. В 1865 году Джеймс Максвелл предположил в рамках своей теории[29], что свет — это электромагнитная волна. В 1888 году эта гипотеза была подтверждена экспериментально Генрихом Герцем, обнаружившим радиоволны[30].

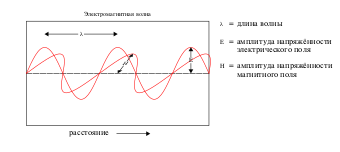
В 1900 году волновая теория Максвелла, рассматривающая электромагнитное излучение как колебания электрического и магнитного полей, выглядела законченной. Однако некоторые эксперименты, проведённые позже, не нашли объяснения в рамках этой теории. Это привело к гипотезе, что энергия световой волны должна излучаться и поглощаться в виде «квантов» величиной hν. Дальнейшие эксперименты показали, что эти световые кванты также обладают импульсом, поэтому оказалось возможным рассматривать их как элементарные частицы

Волновая теория Максвелла не смогла, однако, объяснить всех свойств света. Согласно этой теории, энергия световой волны должна зависеть только от её интенсивности, но не от частоты. На самом же деле результаты некоторых экспериментов показали обратное: переданная от света атомам энергия зависит только от частоты света, а не от интенсивности. Например, некоторые химические реакции могут начаться только при облучении вещества светом, частота которого выше определённого порогового значения; излучение, частота которого ниже этого значения, вне зависимости от интенсивности, не может инициировать реакцию. Аналогично, электроны могут быть вырваны с поверхности металлической пластины только при облучении её светом, частота которого выше определённого значения, так называемой красной границы фотоэффекта; энергия вырванных электронов зависит только от частоты света, но не от его интенсивности[31][32].

Исследования свойств излучения абсолютно чёрного тела, проходившие в течение почти сорока лет (1860—1900)[33], завершились выдвижением гипотезы Макса Планка[34][35] о том, что энергия любой системы при излучении или поглощении электромагнитного излучения частоты [math]\displaystyle{ \nu }[/math] может измениться только на величину, кратную энергии кванта [math]\displaystyle{ E = h\nu }[/math] (то есть дискретно), где [math]\displaystyle{ h }[/math] — постоянная Планка[36]. Альбертом Эйнштейном было показано, что такое представление о квантовании энергии должно быть принято, чтобы объяснить наблюдаемое тепловое равновесие между веществом и электромагнитным излучением[13][14]. На этой же основе им был теоретически описан фотоэлектрический эффект, за эту работу Эйнштейн получил в 1921 году Нобелевскую премию по физике[37]. Напротив, теория Максвелла допускает, что электромагнитное излучение может обладать какой угодно энергией (то есть не квантуется).

Многие физики изначально предполагали, что квантование энергии есть результат какого-то неизвестного свойства материи, поглощающей и излучающей электромагнитные волны. В 1905 году Эйнштейн предположил, что квантование энергии — свойство самого электромагнитного излучения[13]. Признавая справедливость теории Максвелла, Эйнштейн указал, что многие аномальные в то время результаты экспериментов могут быть объяснены, если энергию световой волны поместить в подобные частицам кванты, которые движутся независимо друг от друга, даже если волна непрерывно распространяется в пространстве[13]. В 1909[14] и 1916 годах[16] Эйнштейн показал, исходя из справедливости закона излучения абсолютно чёрного тела, что квант энергии должен также обладать импульсом [math]\displaystyle{ p=h/\lambda }[/math][38]. Импульс фотона был обнаружен экспериментально[39][40] Артуром Комптоном, за эту работу он получил Нобелевскую премию по физике в 1927 году. Однако вопрос согласования волновой теории Максвелла с экспериментальным обоснованием дискретной природы света оставался открытым[41]. Ряд авторов утверждали, что излучение и поглощение электромагнитных волн происходит порциями, квантами, однако процессы распространения волны непрерывны. Квантовый характер явлений излучения и поглощения доказывает наличие у микросистем, в том числе у электромагнитного поля, отдельных энергетических уровней и невозможность микросистемы обладать произвольной величиной энергии. Корпускулярные представления хорошо согласуются с экспериментально наблюдаемыми закономерностями излучения и поглощения электромагнитных волн, в частности, с закономерностями теплового излучения и фотоэффекта. Однако по их мнению экспериментальные данные свидетельствуют, что квантовые свойства электромагнитной волны не проявляются при распространении, рассеянии, дифракции электромагнитных волн, если они не сопровождаются потерей энергии. В процессах распространения электромагнитная волна не находится в определённой точке пространства, ведёт себя как единое целое и описывается уравнениями Максвелла[42]. Решение было найдено в рамках квантовой электродинамики (см. раздел корпускулярно-волновой дуализм ниже) и её преемницы Стандартной модели.

В соответствии с квантовой электродинамикой электромагнитное поле в объёме куба с длиной ребра d можно представить в виде плоских стоячих волн, сферических волн или плоских бегущих волн [math]\displaystyle{ e^{ik{\cdot}x}. }[/math] Объём при этом считается заполненным фотонами с распределением энергии [math]\displaystyle{ n\hbar\omega }[/math], где n — целое число. Взаимодействие фотонов с веществом приводит к изменению числа фотонов n на [math]\displaystyle{ \pm1 }[/math] (излучение или поглощение).

Попытки сохранить теорию Максвелла

До 1923 года большинство физиков отказывалось принимать идею о том, что электромагнитное излучение обладает квантовыми свойствами. Вместо этого они были склонны объяснять поведение фотонов квантованием материи, как, например, в теории Бора для атома водорода. Хотя все эти полуклассические модели были лишь первыми приближениями и выполнялись только для простых систем, они привели к созданию квантовой механики

Как упомянуто в нобелевской лекции Роберта Милликена, предсказания, сделанные в 1905 году Эйнштейном, были проверены экспериментально несколькими независимыми способами в первые два десятилетия XX века[43]. Тем не менее, до знаменитого эксперимента Комптона[39] идея квантовой природы электромагнитного излучения не была среди физиков общепринятой (см. например, Нобелевские лекции Вильгельма Вина[33], Макса Планка[35] и Роберта Милликена[43]), что было связано с успехами волновой теории света Максвелла. Некоторые физики считали, что квантование энергии в процессах излучения и поглощения света являлось следствием неких свойств вещества, излучающего или поглощающего свет. Нильс Бор, Арнольд Зоммерфельд и другие разрабатывали модели атома с дискретными уровнями энергии, которые объясняли наличие спектров излучения и поглощения у атомов и, более того, находились в прекрасном согласии с наблюдаемым спектром водорода[44] (правда, получить спектры других атомов в этих моделях не удавалось)[45]. Только рассеяние фотона свободным электроном, не имеющим внутреннего строения, а следовательно, и энергетических уровней, заставило многих физиков признать квантовую природу света.

Однако даже после экспериментов Комптона Бор, Хендрик Крамерс и Джон Слейтер предприняли последнюю попытку спасти классическую максвелловскую волновую модель света, без учёта его квантования, опубликовав так называемую теорию БКС[46]. Для объяснения экспериментальных данных ими были предложены две гипотезы[47]:

  1. Энергия и импульс сохраняются лишь статистически (в среднем) во взаимодействиях между веществом и излучением. В отдельных элементарных процессах, таких как излучение и поглощение, законы сохранения энергии и импульса не выполняются.
    Это предположение позволило согласовать ступенчатость изменения энергии атома (переходы между энергетическими уровнями) с непрерывностью изменения энергии самого излучения.
  2. Механизм излучения носит специфический характер. В частности, спонтанное излучение рассматривалось как излучение, стимулированное «виртуальным» электромагнитным полем.

Однако эксперименты Комптона показали, что энергия и импульс сохраняются точно в элементарных процессах, а также что его расчёты изменения частоты падающего фотона в комптоновском рассеянии выполняются с точностью до 11 знаков. После этого Бор и его соавторы удостоили свою модель «благородных похорон, насколько это было возможно»[41]. Тем не менее, крах модели БКС вдохновил Вернера Гейзенберга на создание матричной механики[48].

Одним из экспериментов, подтверждающим квантование поглощения света, стал опыт Вальтера Боте, проведённый им в 1925 году. В этом опыте тонкая металлическая фольга облучалась рентгеновским излучением низкой интенсивности. При этом фольга сама становилась источником слабого вторичного излучения. Исходя из классических волновых представлений, это излучение должно распределяться в пространстве равномерно во всех направлениях. В этом случае два счётчика, находившиеся слева и справа от фольги, должны были обнаруживать его одновременно. Однако результат опыта оказался прямо противоположным: излучение засекалось либо правым, либо левым счётчиком и никогда обоими одновременно. Следовательно, поглощение идёт отдельными квантами. Опыт, таким образом, подтвердил исходное положение фотонной теории излучения и стал ещё одним экспериментальным доказательством квантовых свойств электромагнитного излучения[49].

Некоторые физики продолжали разрабатывать полуклассические модели[50], в которых электромагнитное излучение не считалось квантованным, но вопрос получил своё разрешение только в рамках квантовой механики. Идея фотонов при объяснении физических и химических экспериментов стала общепринятой к 70-м годам XX века. Все полуклассические теории большинством физиков стали считаться окончательно опровергнутыми в 70-х и 80-х годах в экспериментах по фотонной корреляции[51]. Таким образом, идея Планка о квантовых свойствах электромагнитного излучения и развитая на её основе гипотеза Эйнштейна считаются доказанными.

Физические свойства фотона

Диаграмма Фейнмана, на которой изображён обмен виртуальным фотоном (обозначен на рисунке волнистой линией) между позитроном и электроном

Фотон — безмассовая нейтральная частица.

Спин фотона равен 1 (частица является бозоном), но из-за нулевой массы покоя более подходящей характеристикой является спиральность, проекция спина частицы на направление движения. Фотон может находиться в двух независимых спиновых состояниях со спиральностью, равной [math]\displaystyle{ \pm 1 }[/math]. Этим состояниям в классической электродинамике соответствует круговая поляризация электромагнитной волны[12]. Как любая квантовая частица, фотон может находиться в суперпозиции состояний с разными спиральностями, таким суперпозициям в классической электродинамике соответствуют другие (эллиптические и линейные) поляризации электромагнитной волны.

Базисные состояния фотона могут описываться одним из двух независимых состояний поляризации и тремя составляющими волнового вектора, который определяет его длину волны [math]\displaystyle{ \lambda }[/math] и направление распространения.

Фотон не имеет электрического заряда. Как любая безмассовая частица фотон не распадается спонтанно в вакууме, а поэтому относится к числу стабильных элементарных частиц[52]. Последнее утверждение справедливо, впрочем, при отсутствии внешнего поля; во внешнем магнитном поле возможен распад фотона на два фотона с другой поляризацией по схеме: [math]\displaystyle{ \gamma \to \gamma+\gamma. }[/math] Такой распад является проявлением нелинейности уравнений Максвелла с учётом радиационных поправок[53].

Массу фотона считают равной нулю, основываясь на эксперименте (отличие массы фотона от нуля привело бы к дисперсии электромагнитных волн в вакууме, что размазало бы по небу наблюдаемые изображения галактик) и теоретических обоснованиях (в квантовой теории поля доказывается, что если бы масса фотона не равнялась нулю, то электромагнитные волны имели бы три, а не два поляризационных состояния)[54]. Поэтому скорость фотона, как и скорость любой безмассовой частицы, равна скорости света. По этой причине (не существует системы отсчёта, в которой фотон покоится) внутренняя чётность частицы не определена[12]. Если приписать фотону наличие т. н. «релятивистской массы» (термин ныне выходит из употребления) исходя из соотношения [math]\displaystyle{ m = \tfrac{E}{c^2}, }[/math] то она составит [math]\displaystyle{ m = \tfrac{h\nu}{c^2}. }[/math]

Фотон — истинно нейтральная частица (т.е. является своей античастицей), поэтому его зарядовая чётность отрицательна и равна −1. Вследствие закона сохранения зарядовой чётности и её мультипликативности в электромагнитных явлениях невозможно превращение чётного числа фотонов в нечётное и наоборот (теорема Фарри)[55].

Фотон относится к калибровочным бозонам. Он участвует в электромагнитном и гравитационном[2] взаимодействии[12].

За счёт участия фотонов в электромагнитном взаимодействии происходят комптоновское рассеяние фотонов на электронах и превращения фотонов достаточно высокой энергии в электромагнитном поле вблизи атомных ядер в электронно-позитронные пары[56]. За счёт участия фотонов в гравитационном взаимодействии происходит гравитационное отклонение света.

Фотон существует часть времени как виртуальная частица (нейтральный векторный мезон) или как виртуальная пара адрон-антиадрон. За счёт этого явления фотон способен участвовать в сильных взаимодействиях. Свидетельством участия фотона в сильных взаимодействиях являются процессы фоторождения пи-мезонов на протонах и нейтронах, а также множественное образование нуклонов на протонах и ядрах. Сечения процессов фоторождения нуклонов на протонах и нейтронах очень близки друг к другу. Это объясняется тем, что у фотона есть адронная составляющая, за счёт чего фотон участвует в сильных взаимодействиях[57][58][59].

Другим свидетельством рождения фотонами виртуальных пар частица-античастица является экспериментальное наблюдение рассеяния фотонов друг на друге, невозможное в рамках классической электродинамики Максвелла[60].

Фотоны излучаются во многих процессах, например, при движении электрически заряженных частиц с ускорением и торможением, при переходе атома, молекулы, иона или атомного ядра из возбуждённого состояния в состояние с меньшей энергией, при распадах элементарных частиц, аннигиляции пары элементарная частица-античастица[61]. При обратных процессах — возбуждение атома, рождение электрон-позитронных пар или других пар частица-античастица — происходит поглощение фотонов[62].

Если энергия фотона равна [math]\displaystyle{ E }[/math], то импульс [math]\displaystyle{ \vec{p} }[/math] связан с энергией соотношением [math]\displaystyle{ E=cp, }[/math] где [math]\displaystyle{ c }[/math] — скорость света (скорость, с которой в любой момент времени движется фотон как безмассовая частица). Для сравнения, для частиц с ненулевой массой покоя связь массы и импульса с энергией определяется формулой [math]\displaystyle{ E^{2}=c^{2}p^{2}+m^{2}c^{4} }[/math], как показано в специальной теории относительности[63].

В вакууме энергия и импульс фотона зависят только от его частоты [math]\displaystyle{ \nu }[/math] (или, что эквивалентно, от длины волны [math]\displaystyle{ \lambda=c/\nu }[/math]):

[math]\displaystyle{ E=\hbar\omega=h\nu, }[/math]
[math]\displaystyle{ \vec{p}=\hbar\vec{k}, }[/math]

и, следовательно, величина импульса есть:

[math]\displaystyle{ p=\hbar k=\frac{h}{\lambda}=\frac{h\nu}{c}, }[/math]

где [math]\displaystyle{ \hbar }[/math] — редуцированная постоянная Планка, равная [math]\displaystyle{ h/2\pi }[/math]; [math]\displaystyle{ \vec{k} }[/math] — волновой вектор и [math]\displaystyle{ k=2\pi/\lambda }[/math] — его величина (волновое число); [math]\displaystyle{ \omega=2\pi\nu }[/math] — угловая частота. Волновой вектор [math]\displaystyle{ \vec{k} }[/math] указывает направление движения фотона. Спин фотона не зависит от частоты.

Классические формулы для энергии и импульса электромагнитного излучения могут быть получены исходя из представлений о фотонах. К примеру, давление излучения осуществляется за счёт передачи импульса фотонов телу при их поглощении. Действительно, давление — это сила, действующая на единицу площади поверхности, а сила равна изменению импульса, отнесённому ко времени этого изменения[64].

В зависимости от электрической и магнитной мультипольности системы зарядов, излучившей данный фотон, для фотона возможны состояния (в какой-либо конкретной системе отсчёта) с полными моментами импульса [math]\displaystyle{ L = 1 \hbar, 2 \hbar, 3 \hbar, ... }[/math] и чётностью −1 или +1. Различают состояния фотонов электрического и магнитного типа. Состояние фотона с моментом [math]\displaystyle{ L }[/math] и чётностью [math]\displaystyle{ (-1)^{L} }[/math] называется фотонным 2L-полем электрического типа, с чётностью [math]\displaystyle{ (-1)^{L+1} }[/math] называется фотонным 2L-полем магнитного типа. Для обозначения фотонов определённой мультипольности сначала пишется буква [math]\displaystyle{ E }[/math] для электрического мультиполя или [math]\displaystyle{ M }[/math] для магнитного мультиполя и вплотную к этой букве пишется цифра, равная полному моменту [math]\displaystyle{ L }[/math]. Электрический дипольный фотон обозначается как [math]\displaystyle{ E1 }[/math], магнитный дипольный — [math]\displaystyle{ M1 }[/math], электрический квадрупольный фотон — [math]\displaystyle{ E2 }[/math], и т. д.[65] Мультипольность фотона не является его внутренним свойством, она определена относительно данной системы отсчёта (например, связанной с излучающей или поглощающей системой зарядов — ядром, атомом и т.п.).

Гипотетические продольные фотоны (являющиеся квантами продольного электромагнитного поля) до сих пор не обнаружены экспериментально, но их существование постулируется в некоторых теориях[66].

Для фотонов локализация частиц имеет физический смысл лишь в условиях применимости понятий геометрической оптики, так как фотон можно локализовать лишь в такой пространственно-временной области [math]\displaystyle{ \Delta x \Delta t }[/math], для которого [math]\displaystyle{ \Delta x \gg \frac{1}{k} }[/math], [math]\displaystyle{ \Delta t \gg \frac{1}{\omega} }[/math], то есть можно применять понятия геометрической оптики[67].

Корпускулярно-волновой дуализм и принцип неопределённости

Основные статьи: Корпускулярно-волновой дуализм и Принцип неопределённости

Фотону свойственен корпускулярно-волновой дуализм. С одной стороны, фотон проявляет свойства электромагнитной волны в явлениях дифракции и интерференции в том случае, если характерные размеры препятствий сравнимы с длиной волны фотона. Например, последовательность одиночных фотонов с частотой [math]\displaystyle{ \nu }[/math], проходящих через двойную щель, создают на экране интерференционную картину, которую можно описать уравнениями Максвелла[68].

Тем не менее эксперименты показывают, что фотоны излучаются и поглощаются целиком объектами, которые имеют размеры, много меньшие длины волны фотона (например, атомами, см. Мазер), или вообще в некотором приближении могут считаться точечными (как, например, электроны). Таким образом, фотоны в процессах излучения и поглощения ведут себя как точечноподобные частицы. Кроме того, фотоны испытывают комптоновское рассеяние на электронах, взаимодействуя с ними как частица в соответствии с законом сохранения энергии и импульса для релятивистских частиц. Фотон также ведёт себя как частица с определённой массой при движении в гравитационном поле поперёк (например, свет звёзд отклоняется Солнцем, как установил, в частности, А. Эддингтон при наблюдении полного солнечного затмения 29 мая 1919 года) или вдоль линии действия силы гравитации, в последнем случае изменяется потенциальная энергия фотона и, следовательно, частота, что было экспериментально установлено в эксперименте Паунда и Ребки[69].

В то же время это описание не является достаточным; представление о фотоне как о точечной частице, чья траектория вероятностно задана электромагнитным полем, опровергается корреляционными экспериментами с запутанными состояниями фотонов, описанными выше (см. также Парадокс Эйнштейна — Подольского — Розена). Также невозможно ввести понятие тока фотонов, для которого выполнялось бы уравнение непрерывности для плотности числа фотонов[70].

Мысленный эксперимент Гейзенберга по определению местонахождения электрона (закрашен синим) с помощью гамма-лучевого микроскопа высокого разрешения. Падающие гамма-лучи (показаны зелёным) рассеиваются на электроне и попадают в апертурный угол микроскопа θ. Рассеянные гамма-лучи показаны на рисунке красным цветом. Классическая оптика показывает, что положение электрона может быть определено только с точностью до определённого значения Δx, которое зависит от угла θ и от длины волны λ падающих лучей

Ключевым элементом квантовой механики является принцип неопределённости Гейзенберга, который запрещает одновременное точное определение пространственной координаты частицы и её импульса по этой координате[71].

Квантование света, а также зависимость энергии и импульса от частоты необходимы для выполнения принципа неопределённости, применённого к заряженной массивной частице. Иллюстрацией этого может служить знаменитый мысленный эксперимент с идеальным микроскопом, определяющим координату электрона путём облучения его светом и регистрации рассеянного света (гамма-микроскоп Гейзенберга). Положение электрона может быть определено с точностью [math]\displaystyle{ \Delta x }[/math], равной разрешающей способности микроскопа. Исходя из представлений классической оптики:

[math]\displaystyle{ \Delta x \sim \frac{\lambda}{\sin \theta}, }[/math]

где [math]\displaystyle{ \theta }[/math] — апертурный угол микроскопа. Таким образом, неопределённость координаты [math]\displaystyle{ \Delta x }[/math] можно сделать сколь угодно малой, уменьшая длину волны [math]\displaystyle{ \lambda }[/math] падающих лучей. Однако после рассеяния электрон приобретает некоторый дополнительный импульс, неопределённость которого равна [math]\displaystyle{ \Delta p }[/math]. Если бы падающее излучение не было квантованным, эту неопределённость можно было бы сделать сколь угодно малой, уменьшая интенсивность излучения. Длину волны и интенсивность падающего света можно менять независимо друг от друга. В результате при отсутствии квантования света стало бы возможным одновременно определить с высокой точностью положение электрона в пространстве и его импульс, что противоречит принципу неопределённости.

Напротив, формула Эйнштейна для импульса фотона полностью удовлетворяет требованиям принципа неопределённости. С учётом того, что фотон может быть рассеян в любом направлении в пределах угла [math]\displaystyle{ \theta }[/math], неопределённость переданного электрону импульса равняется:

[math]\displaystyle{ \Delta p \sim p_{\mathrm{\phi}} \sin\theta = \frac{h}{\lambda} \sin\theta. }[/math]

После умножения первого выражения на второе получается соотношение неопределённостей Гейзенберга: [math]\displaystyle{ \Delta x \Delta p \, \sim \, h. }[/math] Таким образом, весь мир квантован: если вещество подчиняется законам квантовой механики, то и поле должно им подчиняться, и наоборот[72].

Аналогично, принцип неопределённости для фотонов запрещает одновременное точное измерение числа [math]\displaystyle{ n }[/math] фотонов (см. фоковское состояние и раздел вторичное квантование ниже) в электромагнитной волне и фазы [math]\displaystyle{ \varphi }[/math] этой волны (см. когерентное состояние и сжатое когерентное состояние):

[math]\displaystyle{ \Delta n \Delta \varphi \gt 1. }[/math]

И фотоны, и частицы вещества (электроны, нуклоны, ядра, атомы и т. д.), обладающие массой покоя, при прохождении через две близко расположенные узкие щели дают похожие интерференционные картины. Для фотонов это явление можно описать с использованием уравнений Максвелла, для массивных частиц используют уравнение Шрёдингера. Можно было бы предположить, что уравнения Максвелла — упрощённый вариант уравнения Шрёдингера для фотонов. Однако с этим не согласны большинство физиков[73][74]. С одной стороны, эти уравнения отличаются друг от друга математически: в отличие от уравнений Максвелла (описывающих поля — действительные функции координат и времени), уравнение Шрёдингера комплексное (его решением является поле, представляющее собой, вообще говоря, комплексную функцию). С другой стороны, понятие вероятностной волновой функции, которая явным образом входит в уравнение Шрёдингера, не может быть применено по отношению к фотону[75] Фотон — безмассовая частица, поэтому он не может быть локализован в пространстве без уничтожения. Формально говоря, фотон не может иметь координатное собственное состояние [math]\displaystyle{ |\mathbf{r} \rangle }[/math] и, таким образом, обычный принцип неопределённости Гейзенберга в виде [math]\displaystyle{ \Delta x \Delta p \, \sim \, h }[/math] к нему неприменим[76].

Были предложены изменённые варианты волновой функции для фотонов[77][78][79][80], но они не стали общепринятыми. Вместо этого в физике используется теория вторичного квантования (квантовая электродинамика), в которой фотоны рассматриваются как квантованные возбуждения электромагнитных мод.

Модель фотонного газа Бозе — Эйнштейна

Основные статьи: Статистика Бозе — Эйнштейна и Газ Бозе

Квантовая статистика, применяемая к системам частиц с целочисленным спином, была предложена в 1924 году индийским физиком Ш. Бозе для квантов света и развита А. Эйнштейном для всех бозонов. Электромагнитное излучение внутри некоторого объёма можно рассматривать как идеальный газ, состоящий из совокупности фотонов, практически не взаимодействующих друг с другом. Термодинамическое равновесие этого фотонного газа достигается путём взаимодействия со стенками полости. Оно наступает тогда, когда стенки излучают в единицу времени столько же фотонов, сколько поглощают[81]. При этом внутри объёма устанавливается определённое распределение частиц по энергиям. Бозе получил планковский закон излучения абсолютно чёрного тела, вообще не используя электродинамику, а просто модифицировав подсчёт квантовых состояний системы фотонов в фазовом пространстве[82]. В частности, было установлено, что число фотонов в абсолютно чёрной полости, энергия которых приходится на интервал от [math]\displaystyle{ \varepsilon }[/math] до [math]\displaystyle{ \varepsilon+d\varepsilon, }[/math] равно[81]:

[math]\displaystyle{ d n (\varepsilon) = \frac{V \varepsilon^2 d \varepsilon}{\pi^2 \hbar^3 c^3 (e^{\varepsilon/kT} - 1)}, }[/math]

где [math]\displaystyle{ V }[/math] — объём полости, [math]\displaystyle{ \hbar }[/math] — постоянная Дирака, [math]\displaystyle{ T }[/math] — температура равновесного фотонного газа (совпадает с температурой стенок).

В состоянии равновесия электромагнитное излучение в абсолютно чёрной полости (так называемое тепловое равновесное излучение, или чернотельное излучение) описывается теми же термодинамическими параметрами, что и обычный газ: объёмом, температурой, энергией, энтропией и др. Излучение оказывает давление [math]\displaystyle{ P }[/math] на стенки, так как фотоны обладают импульсом[81]. Связь этого давления с температурой отражена в уравнении состояния фотонного газа:

[math]\displaystyle{ P = \frac{1}{3} \sigma T^4, }[/math]

где [math]\displaystyle{ \sigma }[/math] — постоянная Стефана — Больцмана.

Эйнштейн показал, что эта модификация эквивалентна признанию того, что фотоны строго тождественны друг другу, а между ними подразумевается наличие «таинственного нелокального взаимодействия»[83][84], сейчас понимаемого как требование симметричности квантовомеханических состояний относительно перестановки частиц. Эта работа в конечном счёте привела к созданию концепции когерентных состояний и способствовала изобретению лазера. В этих же статьях Эйнштейн расширил представления Бозе на элементарные частицы с целым спином (бозоны) и предсказал явление массового перехода частиц вырожденного бозонного газа в состояние с минимальной энергией при понижении температуры до некоторого критического значения (конденсация Бозе — Эйнштейна). Этот эффект в 1995 году наблюдался экспериментально, а в 2001 году авторам эксперимента была присуждена Нобелевская премия[85].

В современном понимании бозоны, коими в том числе являются и фотоны, подчиняются статистике Бозе — Эйнштейна, а фермионы, например, электроны, — статистике Ферми — Дирака[86].

Спонтанное и вынужденное излучение

Основной источник: [87]
Основные статьи: Вынужденное излучение и Лазер
Вынужденное излучение (в котором фотоны как бы «клонируют» себя) было предсказано Эйнштейном и привело к изобретению лазера. Выводы Эйнштейна стимулировали дальнейшее развитие квантовых представлений о природе света, которые привели к статистической интерпретации квантовой механики

В 1916 году Эйнштейн показал, что закон излучения Планка для абсолютно чёрного тела может быть выведен исходя из следующих статистических полуклассических представлений:

  1. Электроны в атомах находятся на дискретных энергетических уровнях;
  2. При переходе электронов между этими уровнями, атомом поглощаются или излучаются фотоны.

Кроме того, полагалось, что излучение и поглощение света атомами происходит независимо друг от друга и что тепловое равновесие в системе сохраняется за счёт взаимодействия с атомами. Рассмотрим полость, находящуюся в тепловом равновесии и заполненную электромагнитным излучением, которое может поглощаться и излучаться веществом стенок. В состоянии теплового равновесия спектральная плотность излучения [math]\displaystyle{ \rho(\nu) }[/math], зависящая от частоты фотона [math]\displaystyle{ \nu }[/math], в среднем не должна зависеть от времени. Это означает, что вероятность излучения фотона любой данной частоты должна быть равна вероятности его поглощения[88].

Эйнштейн начал с постулирования простых соотношений между скоростями реакций поглощения и испускания. В его модели скорость [math]\displaystyle{ R_{ji} }[/math] поглощения фотонов частоты [math]\displaystyle{ \nu }[/math] и перехода атомов с энергетического уровня [math]\displaystyle{ E_{j} }[/math] на вышележащий уровень с энергией [math]\displaystyle{ E_{i} }[/math] пропорциональна числу [math]\displaystyle{ N_{j} }[/math] атомов с энергией [math]\displaystyle{ E_{j} }[/math] и спектральной плотности излучения [math]\displaystyle{ \rho(\nu) }[/math] для окружающих фотонов той же частоты:

[math]\displaystyle{ R_{ji} = N_{j} B_{ji} \rho(\nu). }[/math]

Здесь [math]\displaystyle{ B_{ji} }[/math] — константа скорости реакции поглощения (коэффициент поглощения). Для осуществления обратного процесса есть две возможности: спонтанное излучение фотонов и возврат электрона на нижележащий уровень посредством взаимодействия со случайным фотоном. Согласно описанному выше подходу, соответствующая скорость реакции [math]\displaystyle{ R_{ij} }[/math], характеризующая излучение системой фотонов частоты [math]\displaystyle{ \nu }[/math] и переход атомов с вышележащего уровня энергии [math]\displaystyle{ E_{i} }[/math] на нижележащий с энергией [math]\displaystyle{ E_{j} }[/math], равняется:

[math]\displaystyle{ R_{ij} = N_{i} A_{ij} + N_{i} B_{ij} \rho(\nu). }[/math]

Здесь [math]\displaystyle{ A_{ij} }[/math] — коэффициент спонтанного излучения, [math]\displaystyle{ B_{ij} }[/math] — коэффициент, ответственный за вынужденное излучение под действием случайных фотонов. При термодинамическом равновесии число атомов в энергетическом состоянии [math]\displaystyle{ i }[/math] и [math]\displaystyle{ j }[/math] в среднем должно быть постоянным во времени, следовательно, величины [math]\displaystyle{ R_{ji} }[/math] и [math]\displaystyle{ R_{ij} }[/math] должны быть равны. Кроме того, по аналогии с выводами статистики Больцмана, имеет место отношение:

[math]\displaystyle{ \frac{N_i}{N_j} = \frac{g_i}{g_j}\exp{\frac{E_j-E_i}{kT}}, }[/math]

где [math]\displaystyle{ g_{i,j} }[/math] — кратность вырождения (синоним: статистический вес) энергетических уровней [math]\displaystyle{ i }[/math] и [math]\displaystyle{ j }[/math], [math]\displaystyle{ E_{i,j} }[/math] — энергия этих уровней, [math]\displaystyle{ k }[/math] — постоянная Больцмана, [math]\displaystyle{ T }[/math] — температура системы. Из сказанного следует вывод, что [math]\displaystyle{ g_i B_{ij} = g_j B_{ji} }[/math] и:

[math]\displaystyle{ A_{ij} = \frac{8 \pi h \nu^{3}}{c^{3}} B_{ij}. }[/math]

Коэффициенты [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] называют коэффициентами Эйнштейна[89].

Эйнштейну не удалось полностью объяснить все эти уравнения, но он считал, что в будущем станет возможным рассчитать коэффициенты [math]\displaystyle{ A_{ij}, }[/math] [math]\displaystyle{ B_{ji} }[/math] и [math]\displaystyle{ B_{ij}, }[/math] когда «механика и электродинамика будут изменены так, чтобы соответствовать квантовой гипотезе»[90]. И это действительно произошло. В 1926 году Поль Дирак получил константу [math]\displaystyle{ B_{ij}, }[/math] используя полуклассический подход[91], а в 1927 успешно нашёл все эти константы, исходя из основополагающих принципов квантовой теории[92][93]. Эта работа стала фундаментом квантовой электродинамики, то есть теории квантования электромагнитного поля. Подход Дирака, названный методом вторичного квантования, стал одним из основных методов квантовой теории поля[94][95][96]. В ранней квантовой механике только частицы вещества, а не электромагнитное поле, трактовались как квантовомеханические.

Эйнштейн был обеспокоен тем, что его теория казалась неполной, в силу того, что она не описывала направление спонтанного излучения фотона. Вероятностная природа движения световых частиц была впервые рассмотрена Исааком Ньютоном в его объяснении явления двойного лучепреломления (эффект расщепления в анизотропных средах луча света на две составляющие) и, вообще говоря, явления расщепления пучков света границей двух сред на отражённый и преломлённый пучки. Ньютон предположил, что «скрытые переменные», характеризующие световые частицы, определяют, в какой из двух расщеплённых лучей пойдёт данная частица[26] Аналогично и Эйнштейн, начиная дистанцироваться от квантовой механики, надеялся на возникновение более общей теории микромира, в которой не будет места случайности[41]. Примечательно, что введение Максом Борном вероятностной интерпретации волновой функции[97][98] было стимулировано поздней работой Эйнштейна, который искал более общую теорию[99].

Вторичное квантование

Основные статьи: Квантовая теория поля и Вторичное квантование
Различные электромагнитные моды (например, изображённые на рисунке) могут быть рассмотрены как независимые квантовые гармонические осцилляторы. Каждый фотон соответствует единичной энергии E = hν в своей электромагнитной моде

В 1910 году Петер Дебай получил формулу Планка, исходя из относительно простого предположения[100]. Он разложил электромагнитное поле в абсолютно чёрной полости по Фурье-модам и предположил, что энергия каждой моды является целым кратным величины [math]\displaystyle{ h\nu, }[/math] где [math]\displaystyle{ \nu }[/math] — соответствующая данной моде частота. Геометрическая сумма полученных мод представляла собой закон излучения Планка. Однако, используя этот подход, оказалось невозможным получить верную формулу для флуктуаций энергии теплового излучения. Решить эту задачу удалось Эйнштейну в 1909 году[14].

В 1925 году Макс Борн, Вернер Гейзенберг и Паскуаль Йордан дали несколько иную интерпретацию дебаевского подхода[101]. Используя классические представления, можно показать, что Фурье-моды электромагнитного поля — полная совокупность электромагнитных плоских волн, каждой из которых соответствует свой волновой вектор и своё состояние поляризации, — эквивалентны совокупности невзаимодействующих гармонических осцилляторов. С точки зрения квантовой механики, энергетические уровни таких осцилляторов определяются соотношением [math]\displaystyle{ E = nh\nu, }[/math] где [math]\displaystyle{ \nu }[/math] — частота осциллятора. Принципиально новым шагом стало то, что мода с энергией [math]\displaystyle{ E = nh\nu }[/math] рассматривалась здесь как состояние из [math]\displaystyle{ n }[/math] фотонов. Этот подход позволил получить правильную формулу для флуктуаций энергии излучения абсолютно чёрного тела.

В квантовой теории поля вероятность наступления события вычисляется как квадрат модуля суммы амплитуд вероятностей (комплексных чисел) всех возможных способов, которыми это событие может реализоваться, как на диаграмме Фейнмана, изображённой здесь

Поль Дирак пошёл ещё дальше[92][93]. Он рассматривал взаимодействие между зарядом и электромагнитным полем как небольшое возмущение, которое вызывает переходы в фотонных состояниях, изменяя числа фотонов в модах при сохранении полных энергии и импульса системы. Дирак, исходя из этого, смог получить коэффициенты Эйнштейна [math]\displaystyle{ A_{ij} }[/math] и [math]\displaystyle{ B_{ij} }[/math] из первых принципов и показал, что статистика Бозе — Эйнштейна для фотонов — естественное следствие корректного квантования электромагнитного поля (сам Бозе двигался в противоположном направлении — он получил закон излучения Планка для абсолютно чёрного тела, постулировав статистическое распределение Бозе — Эйнштейна). В то время ещё не было известно, что все бозоны, включая фотоны, подчиняются статистике Бозе — Эйнштейна.

Рассмотренный Дираком второй порядок приближения в рамках теории возмущений вводит понятие виртуального фотона, кратковременного промежуточного состояния электромагнитного поля; электростатическое и магнитное взаимодействия осуществляются посредством обмена такими виртуальными фотонами. В таких квантовых теориях поля амплитуда вероятности наблюдаемых событий вычисляется путём суммирования по всем возможным промежуточным путям, в том числе даже нефизическим; так, виртуальные фотоны не обязаны удовлетворять дисперсионному соотношению [math]\displaystyle{ E=pc, }[/math] выполняющемуся для физических безмассовых частиц, и могут иметь дополнительные поляризационные состояния (у реальных фотонов две поляризации, тогда как у виртуальных — три или четыре, в зависимости от использующейся калибровки).

Хотя виртуальные частицы и, в частности, виртуальные фотоны не могут наблюдаться непосредственно[102], они вносят измеримый вклад в вероятность наблюдаемых квантовых событий. Более того, расчёты во втором и высших порядках теории возмущений иногда приводят к появлению бесконечно больших значений для некоторых физических величин. Для устранения этих нефизических бесконечностей в квантовой теории поля разработан метод перенормировки[103][104]. Другие виртуальные частицы также могут вносить вклад в сумму; например, два фотона могут взаимодействовать косвенно посредством виртуальной электрон-позитронной пары[105][106]. Этот механизм будет лежать в основе работы Международного линейного коллайдера[107].

Математически метод вторичного квантования заключается в том, что квантовая система, состоящая из большого числа тождественных частиц, описывается с помощью волновых функций, в которых роль независимых переменных играют числа заполнения. Вторичное квантование осуществляется введением операторов, увеличивающих и уменьшающих число частиц в данном состоянии (чисел заполнения) на единицу. Эти операторы называют иногда операторами рождения и уничтожения. Математически свойства операторов заполнения и уничтожения задаются перестановочными соотношениями, вид которых определяется спином частиц. При таком описании волновая функция сама становится оператором[108].

В современных физических обозначениях квантовое состояние электромагнитного поля записывается как фоковское состояние, тензорное произведение состояний каждой электромагнитной моды:

[math]\displaystyle{ |n_{k_0}\rangle\otimes|n_{k_1}\rangle\otimes\dots\otimes|n_{k_n}\rangle\dots, }[/math]

где [math]\displaystyle{ |n_{k_i}\rangle }[/math] представляет собой состояние с числом фотонов [math]\displaystyle{ n_{k_i}, }[/math] находящихся в моде [math]\displaystyle{ k_i. }[/math] Создание нового фотона (например, излучённого в атомном переходе) в моде [math]\displaystyle{ k_i }[/math] записывается так:

[math]\displaystyle{ |n_{k_i}\rangle \rightarrow |n_{k_i}+1\rangle. }[/math]

Фотон как калибровочный бозон

Уравнения Максвелла, описывающие свободное электромагнитное поле, могут быть получены из представлений калибровочной теории как следствие выполнения требования локальной калибровочной инвариантности поля относительно преобразования фазы как функции пространственно-временных координат[109][110]. Для электромагнитного поля эта калибровочная симметрия отражает способность комплексных чисел изменять мнимую часть без воздействия на действительную, как в случае с действием или лагранжианом.

Квант такого калибровочного поля должен быть безмассовым незаряженным бозоном, пока симметрия не нарушится. Поэтому фотон (который как раз и является квантом электромагнитного поля) рассматривается в современной физике как безмассовая незаряженная частица с целым спином. Корпускулярная модель электромагнитного взаимодействия приписывает фотону спин, равный ±1; это означает, что спиральность фотона равна [math]\displaystyle{ \pm \hbar. }[/math] С точки зрения классической физики спин фотона можно интерпретировать как параметр, отвечающий за поляризационное состояние света (за направление вращения вектора напряжённости в циркулярно-поляризованной световой волне[111]). Виртуальные фотоны, введённые в рамках квантовой электродинамики, могут также находиться в нефизических поляризационных состояниях[109].

В Стандартной модели фотон является одним из четырёх калибровочных бозонов, осуществляющих электрослабое взаимодействие. Остальные три (W +, W − и Z 0) называются векторными бозонами и отвечают только за слабое взаимодействие. В отличие от фотона, у векторных бозонов есть масса, они обязаны быть массивными вследствие того, что слабое взаимодействие проявляется лишь на очень малых расстояниях, <10−15 см. Однако кванты калибровочных полей должны быть безмассовыми, появление у них массы нарушает калибровочную инвариантность уравнений движения. Выход из этого затруднения был предложен Питером Хиггсом, теоретически описавшим явление спонтанного нарушения электрослабой симметрии. Оно позволяет сделать векторные бозоны тяжёлыми без нарушения калибровочной симметрии в самих уравнениях движения[110].

Объединение фотона с калибровочными W- и Z-бозонами в электрослабом взаимодействии осуществили Шелдон Ли Глэшоу, Абдус Салам и Стивен Вайнберг, за что были удостоены Нобелевской премии по физике в 1979 году[112][113][114].

Важной проблемой квантовой теории поля является включение в единую калибровочную схему и сильного взаимодействия (так называемое «великое объединение»). Однако ключевые следствия посвящённых этому теорий, такие как распад протона, до сих пор не были обнаружены экспериментально[115].

Вклад фотонов в массу системы

Энергия системы, излучающей фотон с частотой [math]\displaystyle{ \nu }[/math], уменьшается на величину [math]\displaystyle{ E=h\nu, }[/math] равную энергии этого фотона. В результате масса системы уменьшается (если пренебречь переданным импульсом) на [math]\displaystyle{ {E}/{c^2} }[/math]. Аналогично, масса системы, поглощающей фотоны, увеличивается на соответствующую величину[116]

В квантовой электродинамике при взаимодействии электронов с виртуальными фотонами вакуума возникают расходимости, которые устраняются при помощи процедуры перенормировки. В результате масса электрона, стоящая в лагранжиане электромагнитного взаимодействия, отличается от экспериментально наблюдаемой массы. Несмотря на определённые математические проблемы, связанные с подобной процедурой, квантовая электродинамика позволяет с очень высокой точностью дать объяснение таких фактов, как аномальный дипольный момент лептонов[117] и сверхтонкая структура лептонных дуплетов (например, у мюония и позитрония)[118].

Тензор энергии-импульса электромагнитного поля отличен от нуля, поэтому фотоны гравитационно воздействуют на другие объекты, в соответствии с общей теорией относительности. И наоборот, фотоны сами испытывают воздействие гравитации других объектов. В отсутствие гравитации траектории фотонов прямолинейны. В гравитационном поле они отклоняются от прямых в связи с искривлением пространства-времени (см., например, гравитационная линза). Кроме этого, в гравитационном поле наблюдается так называемое гравитационное красное смещение (см. эксперимент Паунда и Ребки). Это свойственно не только отдельным фотонам, в точности такой же эффект был предсказан для классических электромагнитных волн в целом[119].

Фотоны в веществе

Основные статьи: Групповая скорость и Фотохимия

Свет распространяется в прозрачной среде со скоростью меньшей, чем [math]\displaystyle{ c }[/math] — скорость света в вакууме. Например, фотонам, испытывающим множество столкновений на пути от солнечного ядра, излучающего энергию, может потребоваться около миллиона лет, чтобы достичь поверхности Солнца[120]. Однако, двигаясь в открытом космосе, такие же фотоны долетают до Земли всего за 8,3 минуты. Величина, характеризующая уменьшение скорости света, называется показателем преломления вещества (обратите внимание, что пример выше с временем движения фотонов от солнечного ядра к поверхности никакого отношения к коэффициенту преломления и собственной скорости фотонов не имеет).

С классической точки зрения замедление может быть объяснено так. Под действием напряжённости электрического поля световой волны валентные электроны атомов среды начинают совершать вынужденные гармонические колебания. Колеблющиеся электроны начинают с определённым временем запаздывания излучать вторичные волны той же частоты и напряжённости, что и у падающего света, которые интерферируют с первоначальной волной, замедляя её[121]. В корпускулярной модели замедление может быть вместо этого описано смешиванием фотонов с квантовыми возмущениями в веществе (квазичастицами, подобными фононам и экситонам) с образованием поляритона. Такой поляритон имеет отличную от нуля эффективную массу, из-за чего уже не в состоянии двигаться со скоростью [math]\displaystyle{ c }[/math]. Эффект взаимодействия фотонов с другими квазичастицами может наблюдаться напрямую в эффекте Рамана и в рассеянии Мандельштама — Бриллюэна[122].

Аналогично, фотоны могут быть рассмотрены как частицы, всегда движущиеся со скоростью света [math]\displaystyle{ c }[/math], даже в веществе, но испытывающие смещение фазы (запаздывание или опережение) из-за взаимодействия с атомами, которые изменяют их длину волны и импульс, но не скорость[123]. Волновые пакеты, состоящие из этих фотонов, перемещаются со скоростью, меньшей [math]\displaystyle{ c }[/math]. С этой точки зрения фотоны как бы «голые», из-за чего рассеиваются на атомах, и их фаза изменяется. Тогда как с точки зрения, описанной в предыдущем абзаце, фотоны «одеты» посредством взаимодействия с веществом и перемещаются без рассеяния и смещения фазы, но с меньшей скоростью.

В зависимости от частоты свет распространяется в веществе с разной скоростью. Это явление в оптике называется дисперсией. При создании определённых условий можно добиться того, что скорость распространения света в веществе станет чрезвычайно малой (так называемый «медленный свет»). Суть метода в том, что используя эффект электромагнитно-индуцированной прозрачности удаётся получить среду с очень узким провалом в её спектре поглощения. При этом в области этого провала наблюдается чрезвычайно крутой ход показателя преломления. То есть на этом участке сочетаются огромная дисперсия среды (с нормальной спектральной зависимостью — возрастанием показателя преломления в сторону роста частоты) и её прозрачностью для излучения. Это обеспечивает значительное снижение групповой скорости света (при некоторых условиях до 0,091 мм/с)[124].

Фотоны также могут быть поглощены ядрами, атомами или молекулами, спровоцировав таким образом переход между их энергетическими состояниями. Показателен классический пример, связанный с поглощением фотонов зрительным пигментом палочек сетчатки родопсином, в состав которого входит ретиналь, производное ретинола (витамина A), ответственного за зрение человека, как было установлено в 1958 году американским биохимиком нобелевским лауреатом Джорджем Уолдом и его сотрудниками[125]. Поглощение фотона молекулой родопсина вызывает реакцию транс-изомеризации ретиналя, что приводит к разложению родопсина. Таким образом, в сочетании с другими физиологическими процессами, энергия фотона преобразуется в энергию нервного импульса[126]. Поглощение фотона может даже вызвать разрушение химических связей, как при фотодиссоциации хлора; такие процессы являются объектом изучения фотохимии[127][128].

Техническое применение

Основные статьи: Применение лазеров и Спектральный анализ

Существует множество технических устройств, которые так или иначе используют в своей работе фотоны. Ниже для иллюстрации приведены лишь некоторые из них.

Гелий-неоновый лазер. Светящийся луч в центре — это электрический разряд, порождающий свечение. Луч проецируется на экран справа в виде светящейся красной точки

Важным техническим устройством, использующим фотоны, является лазер. Его работа основана на явлении вынужденного излучения, рассмотренного выше. Лазеры применяются во многих областях технологии. С помощью обладающих высокой средней мощностью газовых лазеров осуществляются такие технологические процессы, как резка, сварка и плавление металлов. В металлургии они позволяют получить сверхчистые металлы. Сверхстабильные лазеры являются основой оптических стандартов частоты, лазерных сейсмографов, гравиметров и других точных физических приборов. Лазеры с перестраиваемой частотой (например, лазер на красителях) значительно улучшили разрешающую способность и чувствительность спектроскопических методов, позволив достичь наблюдения спектров отдельных атомов и ионов[129].

Лазеры широко используются в быту (лазерные принтеры, DVD, лазерные указки и др.).

Излучение и поглощение фотонов веществом используется в спектральном анализе. Атомы каждого химического элемента имеют строго определённые резонансные частоты, в результате чего именно на этих частотах они излучают или поглощают свет. Это приводит к тому, что спектры излучения и поглощения атомов и состоящих из них молекул индивидуальны, подобно отпечаткам пальцев у людей.

Эмиссионный спектр (спектр излучения) железа

По применяемым методам различают несколько типов спектрального анализа[130]:

  1. Эмиссионный, использующий спектры излучения атомов, реже — молекул. Этот вид анализа предполагает сжигание некоторого количества пробы в пламени газовой горелки, электрической дуге постоянного или переменного тока, электрической высоковольтной искре. Частным случаем эмиссионного анализа является люминесцентный анализ.
  2. Абсорбционный, использующий спектр поглощения, главным образом молекул, но может быть применён и для атомов. Здесь пробу целиком переводят в газообразное состояние и пропускают через неё свет от источника сплошного излучения. На выходе на фоне сплошного спектра наблюдается спектр поглощения испарённого вещества.
  3. Рентгеновский, использующий рентгеновские спектры атомов, а также дифракцию рентгеновских лучей при прохождении их через исследуемый объект для изучения его структуры. Главное достоинство метода в том, что рентгеновские спектры содержат немного линий, что значительно облегчает изучение состава пробы. Среди недостатков можно выделить невысокую чувствительность и сложность аппаратуры.

В качественном спектральном анализе определяется только состав пробы без указания на количественное соотношение компонентов. Последняя проблема решается в количественном спектральном анализе, на основании того, что интенсивность линий в спектре зависит от содержания соответствующего вещества в исследуемой пробе[131]. Таким образом по спектру вещества может быть определён его химический состав. Спектральный анализ — чувствительный метод, он широко применяется в аналитической химии, астрофизике, металлургии, машиностроении, геологической разведке и других отраслях науки.

Работа многих аппаратных генераторов случайных чисел основана на определении местоположения одиночных фотонов. Упрощённый принцип действия одного из них сводится к следующему. Для того, чтобы сгенерировать каждый бит случайной последовательности, фотон направляется на лучеделитель. Для любого фотона существует лишь две равновероятные возможности: пройти лучеделитель или отразиться от его грани. В зависимости от того, прошёл фотон через лучеделитель или нет, следующим битом в последовательность записывается «0» или «1»[132][133].

Фотонный двигатель

Основная статья: Фотонный двигатель

Фотоны имеют импульс, а потому при истекании из ракетного двигателя создают реактивную тягу. В связи с этим их предполагается применять в фотонных ракетных двигателях, при работе которых скорость истечения фотонов будет равна скорости света, соответственно и космические корабли с такими двигателями смогут разгоняться почти до скорости света и летать к далёким звёздам. Однако создание таких космических кораблей и двигателей — дело далёкого будущего, поскольку в настоящее время целый ряд проблем не может быть решён даже в теории.

Последние исследования

Основная статья: Квантовая оптика

В настоящее время считается, что свойства фотонов хорошо поняты с точки зрения теории. Стандартная модель рассматривает фотоны как калибровочные бозоны со спином, равным 1, с нулевой массой[134] и нулевым электрическим зарядом (последнее следует, в частности, из локальной унитарной симметрии U(1) и из опытов по электромагнитному взаимодействию). Однако физики продолжают искать несоответствия между экспериментом и положениями Стандартной модели. Постоянно повышается точность проводимых экспериментов по определению массы и заряда фотонов. Обнаружение хоть сколько-нибудь малой величины заряда или массы у фотонов нанесло бы серьёзный удар по Стандартной модели. Все эксперименты, проведённые до сих пор, показывают, что у фотонов нет ни электрического заряда[6][7][135], ни массы[135][136][137][138][139][140][141][142][143][144][145]. Наибольшая точность, с которой удалось измерить заряд фотона, равна 5⋅10−52 Кл (или 3⋅10−33 e); для массы — 1,1⋅10−52 кг (6⋅10−17 эВ/c2 или 1⋅10−22 me)[135].

Многие современные исследования посвящены применению фотонов в области квантовой оптики. Фотоны кажутся подходящими частицами для создания на их основе сверхпроизводительных квантовых компьютеров. Изучение квантовой запутанности и связанной с ней квантовой телепортации также является приоритетным направлением современных исследований[146]. Кроме этого, идёт изучение нелинейных оптических процессов и систем, в частности, явления двухфотонного поглощения, синфазной модуляции и оптических параметрических осцилляторов. Однако подобные явления и системы преимущественно не требуют использования в них именно фотонов. Они часто могут быть смоделированы путём рассмотрения атомов в качестве нелинейных осцилляторов. Нелинейный оптический процесс спонтанного параметрического рассеяния часто используется для создания перепутанных состояний фотонов[147]. Наконец, фотоны используются в оптической коммуникации, в том числе в квантовой криптографии[148].

См. также

Примечания

  1. ↑ Ширков, 1980, с. 451.
  2. ↑ 2,0 2,1 Удивительный мир внутри атомного ядра. Вопросы после лекции Архивная копия от 15 июля 2015 на Wayback Machine, ФИАН, 11 сентября 2007 года
  3. ↑ Черные дыры Керра помогли физикам взвесить фотоны Архивная копия от 28 декабря 2014 на Wayback Machine (2012)
  4. ↑ Pani Paolo, Cardoso Vitor, Gualtieri Leonardo, Berti Emanuele, Ishibashi Akihiro. Black-Hole Bombs and Photon-Mass Bounds (англ.) // Physical Review Letters. — 2012. — Vol. 109, iss. 13. — P. 131102 (5 p.). — doi:10.1103/PhysRevLett.109.131102.
  5. ↑ Particle Data Group Архивная копия от 25 декабря 2018 на Wayback Machine (2008)
  6. ↑ 6,0 6,1 Kobychev V. V., Popov S. B. Constraints on the photon charge from observations of extragalactic sources (англ.) // Astronomy Letters. — 2005. — Vol. 31. — P. 147—151. — doi:10.1134/1.1883345. — arXiv:hep-ph/0411398. (недоступная ссылка)
  7. ↑ 7,0 7,1 Altschul B. Bound on the Photon Charge from the Phase Coherence of Extragalactic Radiation (англ.) // Physical Review Letters. — 2007. — Vol. 98. — P. 261801.
  8. ↑ Ширков Д. В. Виртуальные частицы // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 282—283. — 707 с. — 100 000 экз.
  9. ↑ Комар А. А., Лебедев А. И. Электромагнитное взаимодействие // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 540—542. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
  10. ↑ Вайнберг С. Первые три минуты / Стивен Вайнберг; [пер. с англ. В. Строкова] — М.: Эксмо, 2011. — 208 с. — ISBN 978-5-699-46169-1 п. Реликтовое излучение, с. 84.
  11. ↑ Детлаф, Яворский, 2005, с. 485—487.
  12. ↑ 12,0 12,1 12,2 12,3 Тагиров Э. А. Фотон // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 826. — 928 с. — 100 000 экз.
  13. ↑ 13,0 13,1 13,2 13,3 13,4 Einstein А. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (trans. A Heuristic Model of the Creation and Transformation of Light) (нем.) // Annalen der Physik : magazin. — 1905. — Bd. 17. — S. 132—148.  (нем.). Английский перевод доступен в Викитеке.
  14. ↑ 14,0 14,1 14,2 14,3 Einstein А. Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung (trans. The Development of Our Views on the Composition and Essence of Radiation) (нем.) // Physikalische Zeitschrift : magazin. — 1909. — Bd. 10. — S. 817—825.  (нем.). Английский перевод доступен в Викитеке.
  15. ↑ Einstein А. Strahlungs-emission und -absorption nach der Quantentheorie (нем.) // Verhandlungen der Deutschen Physikalischen Gesellschaft : magazin. — 1916. — Bd. 18. — S. 318.  (нем.)
  16. ↑ 16,0 16,1 Einstein А. Zur Quantentheorie der Strahlung (нем.) // Mitteilungen der Physikalischen Geselschaft zu Zürich. — 1916. — Bd. 16. — S. 47. Также Physikalische Zeitschrift, 18, 121—128 (1917).  (нем.)
  17. ↑ Редкин Ю. Н. Часть 5. Физика атома, твердого тела и атомного ядра // Курс общей физики. — Киров: ВятГГУ, 2006. — С. 24. — 152 с.
  18. ↑ Фотохимия. Кругосвет. Дата обращения: 8 апреля 2009. Архивировано 11 августа 2011 года.
  19. ↑ Фролов С. Принцип квантового компьютера (недоступная ссылка). Дата обращения: 8 апреля 2009. Архивировано 19 октября 2002 года.
  20. ↑ Илья Леенсон. Льюис, Гильберт Ньютон. Кругосвет. Дата обращения: 13 марта 2009. Архивировано 11 августа 2011 года.
  21. ↑ Lewis G. N. The conservation of photons (англ.) // Nature. — 1926. — Vol. 118. — P. 874—875. (англ.)
  22. ↑ Rashed R. The Celestial Kinematics of Ibn al-Haytham (англ.) // Arabic Sciences and Philosophy[англ.]. — Cambridge University Press, 2007. — Vol. 17, no. 1. — P. 7—55 [19]. — doi:10.1017/S0957423907000355. (англ.)
  23. ↑ Descartes R. Discours de la méthode (Рассуждение о методе) (фр.). — Imprimerie de Ian Maire, 1637.  (фр.)
  24. ↑ Hooke R. Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon… (англ.). — London (UK): Royal Society, 1667. Архивная копия от 2 декабря 2008 на Wayback Machine
  25. ↑ Huygens C. Traité de la lumière (фр.). — 1678.  (фр.). An English translation Архивная копия от 24 сентября 2009 на Wayback Machine is available from Project Gutenberg (проект «Гутенберг»)
  26. ↑ 26,0 26,1 Newton I. Opticks (англ.). — 4th. — Dover (NY): Dover Publications, 1952. — P. Book II, Part III, Propositions XII—XX; Queries 25—29. — ISBN 0-486-60205-2. (англ.)
  27. ↑ Свет. Кругосвет. Дата обращения: 13 марта 2009. Архивировано 11 августа 2011 года.
  28. ↑ Buchwald J. Z. The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century (англ.). — University of Chicago Press, 1989. — ISBN 0-226-07886-8. (англ.)
  29. ↑ Maxwell J. C. A Dynamical Theory of the Electromagnetic Field (англ.) // Philosophical Transactions of the Royal Society of London : journal. — 1865. — Vol. 155. — P. 459—512. — doi:10.1098/rstl.1865.0008. (англ.) Эта статья была опубликована после доклада Максвелла Королевскому обществу 8 декабря 1864 года.
  30. ↑ Hertz H. Über Strahlen elektrischer Kraft (нем.) // Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin). — 1888. — S. 1297—1307.  (нем.)
  31. ↑ Детлаф, Яворский, 2005, с. 490—493.
  32. ↑ Зависимость люминесценции от частоты, с. 276f, фотоэлектрический эффект, раздел 1.4 в книге Alonso M., Finn E. J. Fundamental University Physics Volume III: Quantum and Statistical Physics (англ.). — Addison-Wesley, 1968. — ISBN 0-201-00262-0. (англ.)
  33. ↑ 33,0 33,1 Wien, W. Wilhelm Wien Nobel Lecture (1911). Дата обращения: 16 сентября 2006. Архивировано 11 августа 2011 года. (англ.)
  34. ↑ Planck M. Über das Gesetz der Energieverteilung im Normalspectrum (нем.) // Annalen der Physik. — 1901. — Bd. 4. — S. 553—563. — doi:10.1002/andp.19013090310.  (нем.)
  35. ↑ 35,0 35,1 Planck M. Max Planck’s Nobel Lecture (1920). Дата обращения: 16 сентября 2006. Архивировано 11 августа 2011 года. (англ.)
  36. ↑ Детлаф, Яворский, 2005, с. 485.
  37. ↑ Текст речи Аррениуса для Нобелевской премии по физике 1921 года (англ.). The Nobel Foundation (10 декабря 1922). Дата обращения: 13 марта 2009. Архивировано 11 августа 2011 года.
  38. ↑ Детлаф, Яворский, 2005, с. 495.
  39. ↑ 39,0 39,1 Compton A. A Quantum Theory of the Scattering of X-rays by Light Elements (англ.) // Physical Review. — 1923. — Vol. 21. — P. 483—502. — doi:10.1103/PhysRev.21.483. Архивировано 11 марта 2008 года. (англ.)
  40. ↑ Детлаф, Яворский, 2005, с. 497—500.
  41. ↑ 41,0 41,1 41,2 Pais, A. Subtle is the Lord: The Science and the Life of Albert Einstein (англ.). — Oxford University Press, 1982. — ISBN 0-198-53907-X. Архивная копия от 31 мая 2012 на Wayback Machine (англ.)
  42. ↑ Китайгородский А. И. Введение в физику. — 5-е изд. — М.: Наука, 1973. — 688 с.
  43. ↑ 43,0 43,1 Robert A. Millikan’s Nobel Lecture. Дата обращения: 16 сентября 2006. Архивировано 11 августа 2011 года. (англ.) Опубликовано 23 мая 1924 года.
  44. ↑ Редкин Ю. Н. Часть 5. Физика атома, твердого тела и атомного ядра // Курс общей физики. — Киров: ВятГГУ, 2006. — С. 12—13. — 152 с.
  45. ↑ Атома строение (недоступная ссылка). Кругосвет. Дата обращения: 13 марта 2009. Архивировано 11 августа 2011 года.
  46. ↑ Bohr N., Kramers H. A., Slater J. C. The Quantum Theory of Radiation (англ.) // Philosophical Magazine. — 1924. — Vol. 47. — P. 785—802. (англ.) Также Zeitschrift für Physik, 24, 69 (1924).
  47. ↑ Кудрявцев П. С. Курс истории физики. — 2-е изд. — М.: Просвещение, 1982. — 448 с. Архивная копия от 22 июня 2008 на Wayback Machine Архивированная копия (недоступная ссылка). Дата обращения: 13 марта 2009. Архивировано 22 июня 2008 года.
  48. ↑ Heisenberg W. Heisenberg Nobel lecture (1933). Дата обращения: 11 марта 2009. Архивировано 11 августа 2011 года.
  49. ↑ Мартинсон Л. К., Смирнов Е. В. Фотонный газ и его свойства (недоступная ссылка — история ). Igrflab.ru. Дата обращения: 15 марта 2009. (недоступная ссылка)
  50. ↑ Mandel, L. The case for and against semiclassical radiation theory (англ.) // Progress in Optics[англ.]. — North-Holland, 1976. — Vol. 13. — P. 27—69. (англ.)
  51. ↑ Результаты этих экспериментов не могут быть объяснены классической теорией света, так как в них сказываются антикорреляции, связанные с особенностями квантовых измерений. В 1974 году первый подобный эксперимент был проведён Клаузером, результаты эксперимента выявили нарушение неравенства Коши — Буняковского. В 1977 году Кимбл продемонстрировал подобный эффект для одинаково поляризованных фотонов, проходящих через анализатор. Некоторые из этих фотонов проходили сквозь анализатор, другие отражались, причём абсолютно случайным образом (Паргаманик Л. Э. Природа статистичности в квантовой механике // Концепция целостности: критика буржуазной методологии науки / Под ред. И. З. Цехмистро. — Харьков: Выща школа; Изд-во Харьковского госуниверситета, 1987. — 222 с. — 1000 экз.). Этот подход был упрощён Торном в 2004 году.
  52. ↑ Савельев И. В. . Курс общей физики. — 2-е изд. — М.: Наука, 1982. — Т. 3. — 304 с.
  53. ↑ Берестецкий, Лифшиц, Питаевский, 1989, с. 650—658.
  54. ↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — 240 с.
  55. ↑ Берестецкий, Лифшиц, Питаевский, 1989, с. 360—361.
  56. ↑ Перкинс Д. Введение в физику высоких энергий. — М.: Мир, 1975. — С. 28.
  57. ↑ Денисов С. П. Превращение излучения в вещество // Соросовский образовательный журнал. — 2000. — Вып. 4. — С. 84—89.
  58. ↑ Фейнман Р. Взаимодействие фотонов с адронами. — М.: Мир, 1975.
  59. ↑ Тагиров Э. А. Фотон // Физика микромира : маленькая энциклопедия / Гл. ред. Д. В. Ширков. — М.: Советская энциклопедия, 1980. — 528 с. — 50 000 экз.
  60. ↑ Aaboud M. et al. (ATLAS Collaboration). Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC (англ.) // Nature Physics. — 2017. — 14 August (vol. 13, no. 9). — P. 852—858. — ISSN 1745-2473. — doi:10.1038/nphys4208. Архивировано 12 июня 2020 года.
  61. ↑ Заметим, что при аннигиляции излучается минимум два фотона, а не один, поскольку в системе центра масс сталкивающихся частиц их суммарный импульс равен нулю, а один излучённый фотон всегда будет иметь ненулевой импульс. Закон сохранения импульса требует излучения, как минимум, двух фотонов с нулевым общим импульсом. Энергия фотонов, а, следовательно, и их частота, определяется законом сохранения энергии.
  62. ↑ Этот процесс является преобладающим при распространении гамма-лучей высоких энергий через вещество.
  63. ↑ Александр Берков. Относительности теория специальная (недоступная ссылка). Кругосвет. Дата обращения: 13 марта 2009. Архивировано 15 марта 2007 года.
  64. ↑ См., например, Appendix XXXII в Born M. Atomic Physics (англ.). — Blackie & Son, 1962.
  65. ↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — 670 с.
  66. ↑ Горелик В. С. Продольные и скалярные бозоны в материальных средах и в вакууме // Вестник Московского государственного технического университета им. Н. Э. Баумана. — Серия: Естественные науки. — 2015. — № 1 (58). — С. 36-55.
  67. ↑ Тирринг В. Е. Принципы квантовой электродинамики. — М.: Высшая школа, 1964. — С. 133.
  68. ↑ Taylor G. I. Interference fringes with feeble light (англ.) // Proceedings of the Cambridge Philosophical Society. — 1909. — Vol. 15. — P. 114—115.
  69. ↑ Ландсберг Г. С. § 209. Квантовые и волновые свойства фотона // Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 497—504. — 656 с. — ISBN 5922103512.
  70. ↑ Берестецкий, Лифшиц, Питаевский, 1989, с. § 3, c. 26—27 и § 4, c. 29.
  71. ↑ Фейнман Р., Лейтон Р., Сэндс М. 3 — излучение, волны, кванты; 4 — кинетика, теплота, звук // Фейнмановские лекции по физике. — 3-е изд. — М.: Мир, 1976. — Т. 1. — С. 218—220. — 496 с.
  72. ↑ См., например, с. 10f в Schiff L. I. Quantum Mechanics. — 3rd Ed. — McGraw-Hill, 1968. — ISBN 0070552878.
  73. ↑ Kramers H. A. Quantum Mechanics (англ.). — Amsterdam: North-Holland, 1958.
  74. ↑ Bohm D. Quantum Theory (англ.). — Dover Publications, 1989. — ISBN 0-486-65969-0.
  75. ↑ Newton T. D., Wigner E. P. Localized states for elementary particles (англ.) // Reviews of Modern Physics. — 1949. — Vol. 21. — P. 400—406. — doi:10.1103/RevModPhys.21.400.
  76. ↑ Берестецкий, Лифшиц, Питаевский, 1989, с. § 5, c. 29.
  77. ↑ Bialynicki-Birula I. On the wave function of the photon (англ.) // Acta Physica Polonica A. — 1994. — Vol. 86. — P. 97—116.
  78. ↑ Sipe J. E. Photon wave functions (англ.) // Physical Review A. — 1995. — Vol. 52. — P. 1875—1883. — doi:10.1103/PhysRevA.52.1875.
  79. ↑ Bialynicki-Birula I. Photon wave function (англ.) // Progress in Optics. — 1996. — Vol. 36. — P. 245—294. — doi:10.1016/S0079-6638(08)70316-0.
  80. ↑ Scully M. O., Zubairy M. S. Quantum Optics (англ.). — Cambridge (UK): Cambridge University Press, 1997. — ISBN 0-521-43595-1. Архивная копия от 8 марта 2020 на Wayback Machine
  81. ↑ 81,0 81,1 81,2 Василевский А. С., Мултановский В. В. Статистическая физика и термодинамика. — М.: Просвещение, 1985. — С. 163—167. — 256 с.
  82. ↑ Bose S. N. Plancks Gesetz und Lichtquantenhypothese (нем.) // Zeitschrift für Physik. — 1924. — Bd. 26. — S. 178—181. — doi:10.1007/BF01327326.
  83. ↑ Einstein A. Quantentheorie des einatomigen idealen Gases (нем.) // Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. — 1924. — Bd. 1924. — S. 261—267.
  84. ↑ Einstein A. Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung (нем.) // Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse. — 1925. — Bd. 1925. — S. 3—14.
  85. ↑ Anderson M. H. et al. Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor (англ.) // Science. — 1995. — Vol. 269. — P. 198—201. — doi:10.1126/science.269.5221.198. — PMID 17789847.
  86. ↑ Streater R. F., Wightman A. S. PCT, Spin and Statistics, and All That (англ.). — Addison-Wesley, 1989. — ISBN 020109410X.
  87. ↑ Р. Фейнман, Р. Лейтон, М. Сэндс. 3 — излучение, волны, кванты; 4 — кинетика, теплота, звук // Фейнмановские лекции по физике. — 3-е изд. — М.: Мир, 1976. — Т. 1. — С. 311—315. — 496 с.
  88. ↑ Einstein A. Strahlungs-emission und -absorption nach der Quantentheorie (нем.) // Verhandlungen der Deutschen Physikalischen Gesellschaft. — 1916. — Bd. 18. — S. 318—323.
  89. ↑ См. Section 1.4 в кн.: Wilson J., Hawkes F. J. B. Lasers: Principles and Applications (англ.). — New York: Prentice Hall, 1987. — ISBN 0-13-523705-X.
  90. ↑ См. с. 322 в статье: Einstein A. Strahlungs-emission und -absorption nach der Quantentheorie (нем.) // Verhandlungen der Deutschen Physikalischen Gesellschaft. — 1916. — Bd. 18. — S. 318—323.:

    Die Konstanten [math]\displaystyle{ A^n_m }[/math] and [math]\displaystyle{ B^n_m }[/math] würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären."
  91. ↑ Dirac P. A. M. On the Theory of Quantum Mechanics (англ.) // Proceedings of the Royal Society A. — 1926. — Vol. 112. — P. 661—677. — doi:10.1098/rspa.1926.0133.
  92. ↑ 92,0 92,1 Dirac P. A. M. The Quantum Theory of the Emission and Absorption of Radiation (англ.) // Proceedings of the Royal Society A. — 1927. — Vol. 114. — P. 243—265.
  93. ↑ 93,0 93,1 Dirac P. A. M. The Quantum Theory of Dispersion (англ.) // Proceedings of the Royal Society A. — 1927. — Vol. 114. — P. 710—728.
  94. ↑ Heisenberg W., Pauli W. Zur Quantentheorie der Wellenfelder (нем.) // Zeitschrift für Physik. — 1929. — Bd. 56. — S. 1. — doi:10.1007/BF01340129.
  95. ↑ Heisenberg W., Pauli W. Zur Quantentheorie der Wellenfelder (нем.) // Zeitschrift für Physik. — 1930. — Bd. 59. — S. 139. — doi:10.1007/BF01341423.
  96. ↑ Fermi E. Quantum Theory of Radiation (англ.) // Reviews of Modern Physics. — 1932. — Vol. 4. — P. 87. — doi:10.1103/RevModPhys.4.87.
  97. ↑ Born M. Zur Quantenmechanik der Stossvorgänge (нем.) // Zeitschrift für Physik. — 1926. — Bd. 37. — S. 863—867. — doi:10.1007/BF01397477.
  98. ↑ Born M. Zur Quantenmechanik der Stossvorgänge (нем.) // Zeitschrift für Physik. — 1926. — Bd. 38. — S. 803. — doi:10.1007/BF01397184.
  99. ↑ «Борн утверждал, что он был вдохновлён неопубликованными попытками Эйнштейна развить теорию, в которой точечноподобные фотоны вероятностно управлялись „полями-призраками“, подчинявшимися уравнениям Максвелла» (Pais A. Inward Bound: Of Matter and Forces in the Physical World (англ.). — Oxford University Press, 1986. — ISBN 0-198-51997-4.).
  100. ↑ Debye P. Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung (нем.) // Annalen der Physik. — 1910. — Bd. 33. — S. 1427—1434. — doi:10.1002/andp.19103381617.
  101. ↑ Born M., Heisenberg W., Jordan P. Quantenmechanik II (нем.) // Zeitschrift für Physik. — 1925. — Bd. 35. — S. 557—615. — doi:10.1007/BF01379806.
  102. ↑ Ефремов А. В. Виртуальные частицы // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 78. — 928 с. — 100 000 экз.
  103. ↑ Григорьев В. И. Возмущений теория // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 82. — 928 с. — 100 000 экз.
  104. ↑ Ефремов А. В. Перенормировка (ренормировка) // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 526—527. — 928 с. — 100 000 экз.
  105. ↑ Ициксон К., Зюбер Ж.-Б. 7.3.1. Рассеяние фотона на фотоне // Квантовая теория поля / Пер. с англ. под ред. Р. М. Мир-Касимова.. — М.: Мир, 1984. — Т. 1. — С. 427—431. — 448 с. — 8000 экз. Архивная копия от 15 сентября 2018 на Wayback Machine
  106. ↑ Ициксон К., Зюбер Ж.-Б. 8.2. Перенормировка // Квантовая теория поля / Пер. с англ. под ред. Р. М. Мир-Касимова.. — М.: Мир, 1984. — Т. 2. — С. 22—43. — 400 с. — 8000 экз. Архивная копия от 15 сентября 2018 на Wayback Machine
  107. ↑ Weiglein G. Electroweak Physics at the ILC (англ.) // Journal of Physics: Conference Series. — 2008. — Vol. 110. — P. 042033. — doi:10.1088/1742-6596/110/4/042033.
  108. ↑ Ефремов А. В. Вторичное квантование // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 94. — 928 с. — 100 000 экз.
  109. ↑ 109,0 109,1 Райдер Л. Квантовая теория поля / Пер. с англ. С. И. Азакова под ред. Р. А. Мир-Касимова. — Волгоград: Платон, 1998. — 512 с. — ISBN 5-66022-361-3.
  110. ↑ 110,0 110,1 Ефремов А. В. Калибровочная симметрия // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 237—239. — 928 с. — 100 000 экз.
  111. ↑ Редкин Ю. Н. Часть 4. Оптика // Курс общей физики. — Киров: ВятГГУ, 2003. — С. 80. — 132 с.
  112. ↑ Sheldon Glashow Nobel lecture Архивная копия от 18 апреля 2008 на Wayback Machine, delivered 8 December 1979.
  113. ↑ Abdus Salam Nobel lecture Архивная копия от 18 апреля 2008 на Wayback Machine, delivered 8 December 1979.
  114. ↑ Steven Weinberg Nobel lecture Архивная копия от 18 апреля 2008 на Wayback Machine, delivered 8 December 1979.
  115. ↑ Глава 14 в Hughes I. S. Elementary particles (англ.). — 2nd Ed. — Cambridge University Press, 1985. — ISBN 0-521-26092-2.
  116. ↑ Раздел 10.1 в Dunlap R. A. An Introduction to the Physics of Nuclei and Particles (англ.). — Brooks/Cole, 2004. — ISBN 0-534-39294-6.
  117. ↑ Ициксон К., Зюбер Ж.-Б. 7.2.1. Эффективное взаимодействие и аномальный магнитный момент // Квантовая теория поля / Пер. с англ. под ред. Р. М. Мир-Касимова.. — М.: Мир, 1984. — Т. 1. — С. 418—421. — 448 с. — 8000 экз. Архивная копия от 15 сентября 2018 на Wayback Machine
  118. ↑ Ициксон К., Зюбер Ж.-Б. 10.3. Сверхтонкое расщепление в позитронии // Квантовая теория поля / Пер. с англ. под ред. Р. М. Мир-Касимова.. — М.: Мир, 1984. — Т. 2. — С. 151—168. — 400 с. — 8000 экз. Архивная копия от 15 сентября 2018 на Wayback Machine
  119. ↑ Разделы 9.1 (гравитационный вклад фотонов) и 10.5 (влияние гравитации на свет) в Stephani H., Stewart J. General Relativity: An Introduction to the Theory of Gravitational Field (англ.). — Cambridge University Press, 1990. — ISBN 0-521-37941-5.
  120. ↑ Naeye R. Through the Eyes of Hubble: Birth, Life and Violent Death of Stars (англ.). — CRC Press, 1998. — P. 16. — ISBN 0-750-30484-7. Архивная копия от 23 ноября 2016 на Wayback Machine
  121. ↑ Касьянов, В. А. Физика 11 класс. — 3-е изд. — М.: Дрофа, 2003. — С. 228—229. — 416 с. — ISBN 5-7107-7002-7.
  122. ↑ Поляритоны в разделе 10.10.1, рассеяние Рамана и Бриллюэна в разделе 10.11.3 Patterson J. D., Bailey B. C. Solid-State Physics: Introduction to the Theory (англ.). — Springer, 2007. — ISBN 3-540-24115-9.
  123. ↑ Ch 4 in Hecht E. Optics (англ.). — Addison Wesley, 2001. — ISBN 9780805385663.
  124. ↑ Е. Б. Александров, В. С. Запасский. Медленный свет: за фасадом сенсации. Элементы.Ру. Дата обращения: 5 апреля 2009. Архивировано 21 августа 2011 года.
  125. ↑ УОЛД (Wald), Джордж. Электронная библиотека «Наука и техника» (4 мая 2001). Дата обращения: 5 апреля 2009. Архивировано 9 сентября 2011 года.
  126. ↑ И. Б. Федорович. Родопсин // Большая советская энциклопедия.
  127. ↑ Раздел 11-5C в Pine, S. H.; Hendrickson, J. B.; Cram, D. J.; Hammond, G. S. Organic Chemistry (неопр.). — 4th. — McGraw-Hill Education, 1980. — ISBN 0-07-050115-7. (англ.)
  128. ↑ Нобелевская лекция Джорджа Уолда, 12 декабря 1967 года The Molecular Basis of Visual Excitation Архивная копия от 23 апреля 2016 на Wayback Machine (англ.).
  129. ↑ Жаботинский М. Е. Лазер // Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1983. — С. 337—340. — 928 с. — 100 000 экз.
  130. ↑ А. А. Бабушкин, П. А. Бажулин, Ф. А. Королев, Л. В. Левшин, В. К. Прокофьев, А. Р. Стриганов. Методы спектрального анализа. — М.: Издательство Московского университета, 1962. — С. 6—20. — 510 с.
  131. ↑ Спектральный анализ. Chemport.ru. Дата обращения: 8 февраля 2009. Архивировано 7 ноября 2011 года.
  132. ↑ Jennewein T. et al. A fast and compact quantum random number generator (англ.) // Review of Scientific Instruments. — 2000. — Vol. 71. — P. 1675—1680. — doi:10.1063/1.1150518.
  133. ↑ Stefanov A. et al. Optical quantum random number generator (англ.) // Journal of Modern Optics. — 2000. — Vol. 47. — P. 595—598. — doi:10.1080/095003400147908.
  134. ↑ Именно из-за отсутствия у фотона массы, ему необходимо двигаться в вакууме с максимально возможной скоростью — скоростью света. Он может существовать лишь в таком движении. Любая остановка фотона равносильна его поглощению
  135. ↑ 135,0 135,1 135,2 γ Mass. γ Charge. Архивная копия от 15 сентября 2018 на Wayback Machine In: M. Tanabashi et al. (Particle Data Group). 2018 Review of Particle Physics (англ.) // Phys. Rev. D. — 2018. — Vol. 98. — P. 030001.
  136. ↑ Spavieri G., Rodriguez M. Photon mass and quantum effects of the Aharonov-Bohm type (англ.) // Physical Review A. — 2007. — Vol. 75. — P. 052113. — doi:10.1103/PhysRevA.75.052113.
  137. ↑ Goldhaber A. S. Terrestrial and Extraterrestrial Limits on The Photon Mass (англ.) // Reviews of Modern Physics. — 1971. — Vol. 43. — P. 277—296. — doi:10.1103/RevModPhys.43.277.
  138. ↑ Fischbach E. et al. New Geomagnetic Limits on the Photon Mass and on Long-Range Forces Coexisting with Electromagnetism (англ.) // Physical Review Letters. — 1994. — Vol. 73. — P. 514—517. — doi:10.1103/PhysRevLett.73.514.
  139. ↑ Davis L., Goldhaber A. S., Nieto M. M. Limit on Photon Mass Deduced from Pioneer-10 Observations of Jupiter’s Magnetic Field (англ.) // Physical Review Letters. — 1975. — Vol. 35. — P. 1402—1405. — doi:10.1103/PhysRevLett.35.1402.
  140. ↑ Luo J. et al. Determination of the limit of photon mass and cosmic magnetic vector with rotating torsion balance (англ.) // Physical Review A. — 1999. — Vol. 270. — P. 288—292.
  141. ↑ Schaeffer B. E. Severe limits on variations of the speed of light with frequency (англ.) // Physical Review Letters. — 1999. — Vol. 82. — P. 4964—4966. — doi:10.1103/PhysRevLett.82.4964.
  142. ↑ Luo J. et al. New experimental limit on the photon rest mass with a rotating torsion balance (англ.) // Physical Review Letters. — 2003. — Vol. 90. — P. 081801. — doi:10.1103/PhysRevLett.90.081801.
  143. ↑ Williams E. R., Faller J. E., Hill H. A. New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass (англ.) // Physical Review Letters. — 1971. — Vol. 26. — P. 721—724. — doi:10.1103/PhysRevLett.26.721.
  144. ↑ Lakes R. Experimental Limits on the Photon Mass and Cosmic Magnetic Vector Potential (англ.) // Physical Review Letters. — 1998. — Vol. 80. — P. 1826. — doi:10.1103/PhysRevLett.80.1826.
  145. ↑ Adelberger E., Dvali G., Gruzinov A. Photon Mass Bound Destroyed by Vortices (англ.) // Physical Review Letters. — 2007. — Vol. 98. — P. 010402. — doi:10.1103/PhysRevLett.98.010402.
  146. ↑ Алексей Паевский. Телепортация вышла на поток. Gazeta.ru. Дата обращения: 19 апреля 2009. Архивировано 19 января 2012 года.
  147. ↑ Физика квантовой информации / Под ред. Д. Боумейстера, А. Экерта, А. Цайлингера. — М.: Постмаркет, 2002. — С. 79—85.
  148. ↑ Мария Чехова. Квантовая оптика. Кругосвет. Дата обращения: 19 апреля 2009. Архивировано 21 августа 2011 года.

Литература

  • Clauser J. F. Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect (англ.) // Phys. Rev. D. — 1974. — Vol. 9. — P. 853—860.
  • Kimble H. J., Dagenais M., Mandel L. Photon Anti-bunching in Resonance Fluorescence (англ.) // Phys. Rev. Lett.. — 1977. — Vol. 39. — P. 691.
  • Физика микромира : маленькая энциклопедия / Гл. ред. Д. В. Ширков. — М.: Советская энциклопедия, 1980. — 528 с. — 50 000 экз.
  • Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
  • Ахиезер А. И., Берестецкий В. Б. . Квантовая электродинамика. — М.: Наука, 1969. — 623 с. — 20 000 экз.
  • Grangier P., Roger G., Aspect A. Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences (англ.) // Europhysics Letters. — 1986. — Vol. 1. — P. 501—504.
  • Thorn J. J. et al. Observing the quantum behavior of light in an undergraduate laboratory (англ.) // American Journal of Physics. — 2004. — Vol. 72. — P. 1210—1219.
  • Pais A. Subtle is the Lord: The Science and the Life of Albert Einstein (англ.). — Oxford University Press, 1982. — P. 364—388, 402—415. Интересная история о становлении теории фотона.
  • Нобелевская лекция Рея Глаубера «100 лет кванту света». Дата обращения: 16 сентября 2006. Архивировано 21 августа 2011 года. 8 декабря 2005 года. (англ.) Ещё одно изложение истории фотона, ключевые фигуры, создавшие теорию когерентных состояний фотона.
  • Детлаф А. А., Яворский Б. М. Курс физики. — 5-е изд. — М.: ACADEMA, 2005. — 720 с. — ISBN 5-7695-2312-3.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Фотон&oldid=17189830