Формула Планка

Излучение абсолютно чёрных тел различной температуры по закону Планка

Фо́рмула Пла́нка (зако́н Пла́нка) — формула, описывающая спектральную плотность излучения, которое создаётся абсолютно чёрным телом определённой температуры. Формула была открыта Максом Планком в 1900 году и названа по его фамилии. Её открытие сопровождалось появлением гипотезы о том, что энергия может принимать только дискретные значения. Эта гипотеза некоторое время после открытия не считалась значимой, но, как принято считать, дала рождение квантовой физике.

Формула

Формула Планка — выражение для спектральной плотности излучения, создаваемого абсолютно чёрным телом определённой температуры. Встречаются различные формы записи этой формулы.

Энергетическая яркость

Формула, выражающая спектральную плотность энергетической яркости, выглядит следующим образом:

[math]\displaystyle{ B_\nu (\nu, T) = \frac{2 h \nu^3}{c^2} \frac{1}{e^\frac{h \nu}{kT} - 1}, }[/math]

где [math]\displaystyle{ \nu }[/math] — частота излучения, [math]\displaystyle{ T }[/math] — температура абсолютно чёрного тела, [math]\displaystyle{ h }[/math] — постоянная Планка, [math]\displaystyle{ c }[/math] — скорость света, [math]\displaystyle{ k }[/math] — постоянная Больцмана. В системе СИ величина [math]\displaystyle{ B_\nu }[/math] в этой формуле имеет размерность Вт·м⁻²·Гц⁻¹·ср⁻¹. Её физический смысл — энергетическая яркость в малом диапазоне частот [math]\displaystyle{ (\nu; \nu + d \nu) }[/math], делённая на [math]\displaystyle{ d \nu }[/math]. Можно использовать аналогичную формулу, в которой энергетическая яркость будет функцией длины волны [math]\displaystyle{ \lambda }[/math], а не частоты:

[math]\displaystyle{ B_\lambda (\lambda, T) = \frac{2 h c^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math].

В этом случае [math]\displaystyle{ B_\lambda }[/math] имеет размерность Вт·м⁻²·м⁻¹·ср⁻¹ и соответствует энергетической яркости в малом диапазоне длин волн [math]\displaystyle{ (\lambda; \lambda + d \lambda) }[/math], делённой на [math]\displaystyle{ d \lambda }[/math].

Излучательная способность

Излучательная способность на частоте [math]\displaystyle{ \nu }[/math] или длине волны [math]\displaystyle{ \lambda }[/math] — это мощность излучения на единицу площади в интервале частот [math]\displaystyle{ (\nu; \nu + d \nu) }[/math] или длин волн [math]\displaystyle{ (\lambda; \lambda + d \lambda) }[/math], делённая, соответственно, на [math]\displaystyle{ d \nu }[/math] или [math]\displaystyle{ d \lambda }[/math]. Она может быть выражена формулами:

[math]\displaystyle{ \varepsilon_\nu (\nu, T) = \frac{2 \pi h \nu^3}{c^2} \frac{1}{e^\frac{h \nu}{kT} - 1} }[/math],

[math]\displaystyle{ \varepsilon_\lambda (\lambda, T) = \frac{2 \pi h c^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math].

Таким образом, излучательная способность тела численно в [math]\displaystyle{ \pi }[/math] раз больше яркости, если телесный угол в ней измеряется в стерадианах. Величины [math]\displaystyle{ \varepsilon_\nu }[/math] и [math]\displaystyle{ \varepsilon_\lambda }[/math] имеют размерности, соответственно, Вт·м⁻²·Гц⁻¹ и Вт·м⁻²·м⁻¹.

Спектральная плотность энергии

Ещё одна форма записи описывает спектральную объёмную плотность энергии излучения абсолютно чёрного тела. По аналогии с предыдущими формулами, она равна плотности энергии в малом диапазоне частот или длин волн, делённой на ширину этого диапазона:

[math]\displaystyle{ u_\nu (\nu, T) = \frac{8 \pi h \nu^3}{c^3} \frac{1}{e^\frac{h \nu}{kT} - 1} }[/math],

[math]\displaystyle{ u_\lambda (\lambda, T) = \frac{8 \pi h c}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math].

В системе СИ величины [math]\displaystyle{ u_\nu }[/math] и [math]\displaystyle{ u_\lambda }[/math] имеют размерности, равные, соответственно, Дж·м⁻³·Гц⁻¹ и Дж·м⁻³·м⁻¹. Кроме того, спектральная плотность энергии связана с излучательной способностью соотношением [math]\displaystyle{ \varepsilon = \frac{c}{4} u }[/math].

Применимость

Спектр Солнца (жёлтый цвет) и спектр абсолютно чёрного тела температурой 5777 K (серый цвет)

Формула Планка применима для излучения, которое находится в тепловом равновесии с веществом при определённой температуре. Она применима для абсолютно чёрных тел любой формы вне зависимости от состава и структуры при условии, что размеры излучающего тела и деталей его поверхности гораздо больше длин волн, на которых тело в основном излучает.

В случае если тело не является абсолютно чёрным, то спектр его равновесного теплового излучения не описывается законом Планка, но связан с ним законом излучения Кирхгофа. Согласно этому закону, отношение излучательной и поглощательной способностей тела одинаково для всех длин волн и зависит только от температуры. Так, например, при одной температуре распределение энергии в спектре абсолютно серого тела будет таким же, как и в спектре абсолютно чёрного, но суммарная энергетическая яркость излучения будет меньше.

Формула Планка также используется и для описания реальных тел, спектр излучения которых отличается от планковского. Для этого вводится понятие эффективной температуры тела: это та температура, при которой абсолютно чёрное тело излучает столько же энергии на единицу площади, что и данное тело. Аналогичным образом определяется яркостная температура, равная температуре абсолютно чёрного тела, излучающего столько же энергии на единицу площади на определённой длине волны, и цветовая температура, равная температуре абсолютно чёрного тела с таким же распределением энергии в определённом участке спектра. Например, для Солнца эффективная температура составляет около 5780 K, а яркостная температура, в зависимости от длины волны, принимает различные значения: на длине волны 1500 Å она достигает минимального значения в 4200 K, а в видимом диапазоне на длине волны 5500 Å составляет около 6400 K, в то время как для абсолютно чёрного тела температуры, определяемые таким образом, совпадают.

История открытия

Предыстория

Определение закона теплового излучения представляло интерес с 1859 года, когда Густав Кирхгоф открыл закон излучения Кирхгофа, согласно которому отношение излучательной и поглощательной способностей универсально для всех тел. Следовательно, функция излучения абсолютно чёрного тела, поглощательная способность которого равна единице для всех длин волн, должна совпадать с функцией этого отношения.

К концу XIX века спектр излучения абсолютно чёрного тела уже был известен экспериментально. В 1896 году Вильгельм Вин эмпирически описал его законом излучения Вина, однако получить ни его теоретическое обоснование, ни какой-либо вывод физикам на тот момент не удавалось. Хотя Вин в своей работе приводил обоснование закона, оно было недостаточно строгим, чтобы эта проблема считалась решённой.

Макс Планк был одним из тех, кто пытался теоретически обосновать закон излучения Вина. Он исходил из того, что излучатели являются линейными гармоническими осцилляторами, у которых установилось равновесие между испусканием и поглощением; определив связь между энтропией и энергией осцилляторов, он смог подтвердить закон излучения Вина.

Однако дальнейшие эксперименты показали, что закон излучения Вина неточно описывает спектр теплового излучения в длинноволновой области. В октябре 1900 года Планк представил формулу, которая с точностью до констант совпадала с современным законом Планка. В тот же день было выяснено, что формула хорошо описывает экспериментальные данные, но при этом она не имела под собой теоретической основы. Планк вывел её лишь на основании того, что в предельном случае для коротких волн она должна переходить в закон Вина, но, в отличие от него, согласовываться с экспериментальными данными для длинных волн.

Открытие

Менее чем через два месяца после сообщения о получении формулы Планк представил её теоретический вывод на заседании Немецкого физического общества. В нём использовалось соотношение для энтропии, введённое Людвигом Больцманом, в котором рассматривается число возможных микроскопических состояний системы. Планк, чтобы иметь возможность использовать методы комбинаторики и оценить таким образом энтропию, сделал допущение, что полная энергия состоит из целого числа конечных элементов энергии — квантов.

Несмотря на то, что в этом выводе появились кванты и была введена и впервые использована постоянная Планка, ни сам Планк, ни его коллеги не поняли всей глубины открытия. Например, Планк считал, что дискретность энергии не имеет никакого физического смысла и является лишь математическим приёмом. Другие физики также не придали этому значения и не считали, что это предположение противоречит классической физике. Лишь после публикации Хендрика Лоренца в 1908 году научное сообщество пришло к мнению, что кванты действительно имеют физический смысл. Сам Планк впоследствии называл ввод квантов «актом отчаяния», вызванным тем, что «теоретическое объяснение должно быть найдено любой ценой, сколь высокой она ни была бы». Несмотря на всё это, день, когда формула Планка была обоснована, — 14 декабря 1900 года — считается днём рождения квантовой физики.

Пользуясь соображениями классической физики, в 1900 году лорд Рэлей, а в 1905 году Джеймс Джинс вывели закон Рэлея — Джинса. К такому же результату, независимо от них, приходил в своих работах и сам Планк. Вывод этого закона мало отличался от вывода закона Планка (см. ниже), за исключением того, что средняя энергия излучения [math]\displaystyle{ \langle\varepsilon\rangle }[/math] была принята равной [math]\displaystyle{ kT }[/math], согласно теореме о равном распределении энергии по степеням свободы. С точки зрения классической физики ход вывода не вызывал сомнений, однако закон Рэлея — Джинса не только серьёзно расходился с экспериментальными данными везде, кроме длинноволновой области, но и предсказывал бесконечно большую мощность излучения на коротких волнах. Этот парадокс указал на то, что в классической физике всё же имеются фундаментальные противоречия, и стал дополнительным аргументом в пользу квантовой гипотезы. Пауль Эренфест в 1911 году впервые назвал его ультрафиолетовой катастрофой.

В 1918 году Макс Планк стал лауреатом Нобелевской премии по физике, и хотя официально он был награждён за открытие квантов, это открытие было тесно связано с выводом закона Планка.

Вывод формулы Планка

Вывод через распределение Больцмана

Формула Планка выводится следующим образом.

При выводе рассматривается абсолютно чёрное тело малых размеров с температурой [math]\displaystyle{ T }[/math], расположенное внутри куба с ребром длины [math]\displaystyle{ l }[/math], внутренние стенки которого идеально отражают излучение. В результате испускание и поглощение света уравновесятся, а излучение будет распределено равномерно по всему внутреннему пространству куба. Внутри куба будет поддерживаться некоторая плотность энергии [math]\displaystyle{ u(T) }[/math]. Тогда спектральной плотностью энергии будет называться величина [math]\displaystyle{ u_{\omega}(\omega, T) }[/math], равная плотности энергии на единичный интервал угловых частот вблизи [math]\displaystyle{ \omega }[/math].

При выборе малой площади [math]\displaystyle{ \Delta S }[/math] на поверхности абсолютно чёрного тела можно рассчитать, сколько энергии на неё падает. Плотность энергии, падающей под углом [math]\displaystyle{ \theta }[/math] к нормали из телесного угла [math]\displaystyle{ d\Omega }[/math], равна [math]\displaystyle{ d\tilde{u} = u(T) \frac{d \Omega}{4 \pi} }[/math], так как излучение равномерно распределено по всем направлениям в телесном угле [math]\displaystyle{ 4 \pi }[/math] стерадиан. Свет движется со скоростью [math]\displaystyle{ c }[/math], а значит, за время [math]\displaystyle{ \Delta t }[/math] на поверхность падает энергия [math]\displaystyle{ dw }[/math]:

[math]\displaystyle{ dw = c \, d \tilde u \, \Delta t \, \Delta S \cos \theta = \frac{c}{4 \pi} u(T) \cos \theta \sin \theta \, d \theta \, d \varphi \, \Delta S \, \Delta t }[/math].

Суммой энергии, приходящей со всех направлений, будет поток [math]\displaystyle{ \Phi }[/math]:

[math]\displaystyle{ \Phi = \frac{c}{4\pi} u(T) \int_0^{2\pi} d \varphi \int_0^{\pi / 2} \cos \theta \sin \theta \, d \theta = \frac{c}{4} u(T) }[/math].

Такое же количество энергии будет излучать та же единица площади абсолютно чёрного тела, а значит, как для всего потока, так и для любого диапазона частот или длин волн будет справедливо соотношение [math]\displaystyle{ \varepsilon = \frac{c}{4} u }[/math].

Так как внутри куба одновременно присутствуют и излучаемые, и отражённые волны, поле теплового излучения должно представлять собой их суперпозицию, то есть иметь вид стоячих электромагнитных волн. Для определения их параметров вводятся декартова система координат вдоль рёбер куба и соответствующие орты [math]\displaystyle{ \vec{e}_x, \vec{e}_y, \vec{e}_z }[/math]. Для волны, которая распространяется строго вдоль оси [math]\displaystyle{ x }[/math], должно выполняться [math]\displaystyle{ l = n_x \frac{\lambda}{2} }[/math], где [math]\displaystyle{ n_x }[/math] — натуральное число: то есть полуцелое число волн должно иметь суммарную длину ровно [math]\displaystyle{ l }[/math]. Волновой вектор такой волны равен [math]\displaystyle{ \vec{k} = k_x \vec{e}_x }[/math], где [math]\displaystyle{ k_x = \frac{2\pi}{\lambda} }[/math] — волновое число, ограничение для которого принимает вид [math]\displaystyle{ k_x = n_x \frac{\pi}{l} }[/math].

Для волн, распространяющихся вдоль осей [math]\displaystyle{ y }[/math] и [math]\displaystyle{ z }[/math], рассуждения аналогичны; волну, которая распространяется в любом другом направлении, можно представлять в виде суперпозиции волн, которые распространяются вдоль осей: [math]\displaystyle{ \vec{k} = k_x \vec{e}_x + k_y \vec{e}_y + k_z \vec{e}_z }[/math]. Следовательно, [math]\displaystyle{ k_x = n_x \frac{\pi}{l}, k_y = n_y \frac{\pi}{l}, k_z = n_z \frac{\pi}{l} }[/math], где [math]\displaystyle{ n_x, n_y, n_z }[/math] — независимые друг от друга натуральные числа либо нули. Тогда волновое число любой волны представляется как [math]\displaystyle{ k = \sqrt{k_x^2 + k_y^2 + k_z^2} = \frac{\pi}{l} \sqrt{n_x^2 + n_y^2 + n_z^2} }[/math], а частота как [math]\displaystyle{ \omega = \frac{\pi c}{l} \sqrt{n_x^2 + n_y^2 + n_z^2} }[/math]. Каждой тройке этих параметров соответствует одна стоячая волна.

С помощью безразмерной величины [math]\displaystyle{ R = \frac{\omega l}{\pi c} }[/math] можно определить число стоячих волн частотой не более [math]\displaystyle{ \omega }[/math]. Это число [math]\displaystyle{ \tilde{N} }[/math] равно числу комбинаций [math]\displaystyle{ n_x, n_y, n_z }[/math], для которых [math]\displaystyle{ R^2 \geq n_x^2 + n_y^2 + n_z^2 }[/math]. Тогда можно оценить [math]\displaystyle{ \tilde{N} }[/math] как восьмую часть объёма шара с радиусом [math]\displaystyle{ R }[/math]:

[math]\displaystyle{ \tilde{N} = \frac{1}{8} \cdot \frac{4}{3}\pi R^3 = \frac{1}{6} \cdot \frac{\omega^3 l^3}{\pi^2 c^3} = \frac{1}{6} \cdot \frac{\omega^3}{\pi^2 c^3} V, }[/math]

где [math]\displaystyle{ V }[/math] — пространство, в котором заключено излучение. Так как электромагнитные волны — поперечные, в каждом направлении могут распространяться по две волны, поляризованных взаимно перпендикулярно, и реальное число волн [math]\displaystyle{ N }[/math] увеличивается ещё в два раза:

[math]\displaystyle{ N = 2 \tilde{N} = \frac{1}{3} \cdot \frac{\omega^3}{\pi^2 c^3} V }[/math].

Если продифференцировать это выражение по частоте, получится число стоячих волн с длинами волн в интервале [math]\displaystyle{ (\omega; \omega + d \omega) }[/math]:

[math]\displaystyle{ dN = \frac{\omega^2 d \omega}{\pi^2 c^3} V }[/math].

Можно взять за [math]\displaystyle{ \langle\varepsilon\rangle }[/math] среднюю энергию стоячей электромагнитной волны с частотой [math]\displaystyle{ \omega }[/math]. Если умножить количество стоячих волн [math]\displaystyle{ dN }[/math] на [math]\displaystyle{ \langle\varepsilon\rangle }[/math] и разделить полученное значение на [math]\displaystyle{ V }[/math] и на [math]\displaystyle{ d \omega }[/math], получится спектральная плотность энергии излучения:

[math]\displaystyle{ u_{\omega} = \frac{\omega^2}{\pi^2 c^3} \langle\varepsilon\rangle }[/math].

Для дальнейшего вывода закона Планка необходимо учитывать эффекты квантовой физики, а именно — то, что энергия излучается конечными по величине порциями, по величине равными [math]\displaystyle{ E = \hbar \omega }[/math] ([math]\displaystyle{ \hbar = \frac{h}{2\pi} }[/math] — постоянная Дирака); соответственно, возможные значения энергии излучения равны [math]\displaystyle{ \varepsilon_n = n\hbar\omega }[/math], где [math]\displaystyle{ n }[/math] — любое натуральное число. Таким образом, средняя энергия излучения [math]\displaystyle{ \langle\varepsilon\rangle }[/math] равна:

[math]\displaystyle{ \langle\varepsilon\rangle = \sum_{n = 0}^\infty P_n \varepsilon_n, }[/math]

где [math]\displaystyle{ P_n }[/math] — вероятность того, что излучение будет иметь энергию, равную [math]\displaystyle{ \varepsilon_n }[/math]. Вероятность описывается распределением Больцмана по энергиям с некоторой константой [math]\displaystyle{ A }[/math]:

[math]\displaystyle{ P_n = Ae^{-\frac{\varepsilon_n}{kT}} }[/math].

С учётом [math]\displaystyle{ \sum_{n = 0}^\infty P_n = 1 }[/math], для [math]\displaystyle{ A }[/math] верно:

[math]\displaystyle{ A = \left(\sum_{n = 0}^\infty e^{-\frac{\varepsilon_n}{kT}}\right)^{-1} }[/math].

Таким образом, [math]\displaystyle{ \langle\varepsilon\rangle }[/math] выражается как:

[math]\displaystyle{ \langle \varepsilon \rangle = \frac{\sum_{n = 0}^{\infty} n\hbar\omega e^{-\frac{n\hbar\omega}{kT}}}{\sum_{n = 0}^{\infty} e^{-\frac{n\hbar\omega}{kT}}} = \hbar\omega \frac{\sum_{n = 0}^{\infty} n e^{-n\xi}}{\sum_{n = 0}^{\infty} e^{-n\xi}} }[/math].

Здесь [math]\displaystyle{ \xi = \frac{\hbar\omega}{kT} }[/math]. Знаменатель раскладывается по формуле суммы геометрической прогрессии, а числитель представляется как производная знаменателя по [math]\displaystyle{ \xi }[/math]:

[math]\displaystyle{ S = \sum_{n = 0}^{\infty} e^{-n \xi} = \frac{1}{1 - e^{-\xi}} }[/math],

[math]\displaystyle{ \sum_{n = 0}^{\infty} ne^{-n \xi} = -\frac{dS}{d\xi} = \frac{e^{-\xi}}{(1 - e^{-\xi})^2} }[/math].

Получается выражение для средней энергии:

[math]\displaystyle{ \langle\varepsilon\rangle = \frac{\hbar\omega}{e^\frac{\hbar\omega}{kT} - 1} }[/math].

Если подставить [math]\displaystyle{ \langle\varepsilon\rangle }[/math] в формулу для спектральной плотности энергии излучения, получится один из окончательных вариантов формулы Планка:

[math]\displaystyle{ u_{\omega} = \frac{\hbar \omega^3}{\pi^2 c^3} \frac{1}{e^\frac{\hbar\omega}{kT} - 1} }[/math].

Соотношение [math]\displaystyle{ \varepsilon = \frac{c}{4} u }[/math] позволяет получить формулу для излучательной способности:

[math]\displaystyle{ \varepsilon_{\omega} = \frac{\hbar \omega^3}{4 \pi^2 c^2} \frac{1}{e^\frac{\hbar\omega}{kT} - 1} }[/math].

Если разделить на [math]\displaystyle{ \pi }[/math], получится выражение для спектральной плотности яркости:

[math]\displaystyle{ B_{\omega} = \frac{\hbar \omega^3}{4 \pi^3 c^2} \frac{1}{e^\frac{\hbar\omega}{kT} - 1} }[/math].

Эти величины можно выразить через другие параметры — например, циклическую частоту [math]\displaystyle{ \nu }[/math] или длину волны [math]\displaystyle{ \lambda }[/math]. Для этого нужно учесть, что по определению выполняются соотношения [math]\displaystyle{ B_\omega d \omega = B_\nu d \nu }[/math], [math]\displaystyle{ B_\nu d \nu = -B_\lambda d \lambda }[/math] (минус появляется из-за того, что про росте длины волны уменьшается частота) и аналогичные формулы для излучательной способности и плотности энергии. Так, для перехода к циклическим частотам нужно заменить [math]\displaystyle{ \omega = 2\pi\nu }[/math] (при этом [math]\displaystyle{ \hbar = \frac{h}{2\pi} }[/math], так что [math]\displaystyle{ h\nu = \hbar\omega }[/math]) и домножить на [math]\displaystyle{ \frac{d \omega}{d \nu} = 2 \pi }[/math], тогда формулы примут вид:

[math]\displaystyle{ u_\nu = \frac{8 \pi h \nu^3}{c^3} \frac{1}{e^\frac{h \nu}{kT} - 1} }[/math],

[math]\displaystyle{ \varepsilon_\nu = \frac{2 \pi h \nu^3}{c^2} \frac{1}{e^\frac{h \nu}{kT} - 1} }[/math],

[math]\displaystyle{ B_\nu = \frac{2 h \nu^3}{c^2} \frac{1}{e^\frac{h \nu}{kT} - 1} }[/math].

Аналогичным образом получаются формулы для длин волн. После замены [math]\displaystyle{ \nu = \frac{c}{\lambda} }[/math] и домножения на [math]\displaystyle{ \frac{d \nu}{d \lambda} = -\frac{c}{\lambda^2} }[/math]:

[math]\displaystyle{ u_\lambda = \frac{8 \pi h c}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math],

[math]\displaystyle{ \varepsilon_\lambda = \frac{2 \pi h c^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math],

[math]\displaystyle{ B_\lambda = \frac{2 h c^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda k T} - 1} }[/math].

Вывод через статистику Бозе — Эйнштейна

Если рассматривать равновесное излучение как фотонный газ, к нему можно применить статистику Бозе — Эйнштейна. Она определяет среднее число частиц [math]\displaystyle{ \langle n_i \rangle }[/math] в [math]\displaystyle{ i }[/math]-м квантовом состоянии с энергией [math]\displaystyle{ E_i }[/math]:

[math]\displaystyle{ \langle n_i \rangle = \frac{1}{e^\frac{E_i - \mu}{kT} - 1} }[/math].

В этой формуле [math]\displaystyle{ \mu }[/math] — химический потенциал газа. Для фотонного газа он равен нулю, поэтому формула для него представима в следующем виде:

[math]\displaystyle{ \langle n \rangle = \frac{1}{e^\frac{\hbar\omega}{kT} - 1} }[/math].

Если умножить среднее число фотонов [math]\displaystyle{ \langle n \rangle }[/math] на их энергию [math]\displaystyle{ \hbar \omega }[/math], получится та же средняя энергия [math]\displaystyle{ \langle \varepsilon \rangle }[/math], что и выведенная из распределения Больцмана. При подстановке её в формулу для спектральной плотности энергии [math]\displaystyle{ u_{\omega} = \frac{\omega^2}{\pi^2 c^3} \langle\varepsilon\rangle }[/math] получится закон Планка.

Вывод через спонтанное и вынужденное излучения

Формула Планка также может быть выведена из рассмотрения механизмов спонтанного и вынужденного излучений атомов.

В этом выводе, предложенном Эйнштейном в 1916 году, рассматриваются [math]\displaystyle{ N_m }[/math] и [math]\displaystyle{ N_n }[/math] атомов на уровнях с энергией [math]\displaystyle{ E_m }[/math] и [math]\displaystyle{ E_n }[/math] соответственно. Тогда количество переходов с высшего уровня [math]\displaystyle{ E_n }[/math] на низший [math]\displaystyle{ E_m }[/math] в единицу времени пропорционально [math]\displaystyle{ N_n }[/math] и может быть записано как [math]\displaystyle{ A^m_n N_n }[/math]. При вынужденном излучении количество переходов в единицу времени пропорционально [math]\displaystyle{ N_n }[/math] и спектральной плотности излучения на частоте перехода [math]\displaystyle{ u(\omega_{mn}) }[/math], то есть может быть записано как [math]\displaystyle{ B^m_n N_n u(\omega_{mn}) }[/math]. Количество же переходов в единицу времени из-за поглощения пропорционально [math]\displaystyle{ N_m }[/math] и [math]\displaystyle{ u(\omega_{mn}) }[/math] и записывается как [math]\displaystyle{ B^n_m N_m u(\omega_{mn}) }[/math].

Величины [math]\displaystyle{ A^m_n, B^m_n, B^n_m }[/math] — характеристики только самого атома и выбранных энергетических уровней, называемые коэффициентами Эйнштейна. Если поле излучения равновесное и имеет температуру [math]\displaystyle{ T }[/math], то условие детального равновесия выглядит следующим образом:

[math]\displaystyle{ A^m_n N_n + B^m_n N_n u(\omega_{mn}) = B^n_m N_m u(\omega_{mn}) }[/math].

В пределе [math]\displaystyle{ T \rightarrow \infty }[/math] можно пренебречь спонтанным излучением по сравнению с вынужденным, и тогда условие равновесия примет вид [math]\displaystyle{ B^m_n N_n = B^n_m N_m }[/math]. Так как при [math]\displaystyle{ T \rightarrow \infty }[/math] будет выполняться [math]\displaystyle{ N_n = N_m }[/math], а коэффициенты Эйнштейна не зависят от температуры, будет верно равенство [math]\displaystyle{ B^m_n = B^n_m }[/math], что справедливо для простых уровней; для кратных уровней нужно дополнительно учитывать коэффициенты кратности. В дальнейшем можно рассматривать только простые уровни, так как плотность энергии излучения не зависит от деталей строения вещества.

Можно воспользоваться распределением Больцмана:

[math]\displaystyle{ \frac{N_n}{N_m} = e^\left(\frac{E_n - E_m}{kT}\right) }[/math].

При применении его к условию равновесия получается:

[math]\displaystyle{ u(\omega_{mn}) = \frac{\alpha(\omega_{mn})}{e^\left(\frac{\hbar \omega_{mn}}{kT}\right) - 1}, }[/math]

где [math]\displaystyle{ \alpha(\omega_{mn}) = \frac{A^m_n}{B^m_n} }[/math]. Эта величина не зависит от температуры и может быть найдена из условия, что для высоких температур должна быть справедлива формула Рэлея — Джинса:

[math]\displaystyle{ u(\omega_{mn}) = \frac{\alpha(\omega_{mn}) kT}{\hbar{\omega_{mn}}} }[/math],

[math]\displaystyle{ \alpha(\omega_{mn}) = \frac{\hbar \omega^3_{mn}}{\pi^2 c^3} }[/math].

Энергетические уровни могут быть взяты произвольным образом, поэтому индексы [math]\displaystyle{ m }[/math] и [math]\displaystyle{ n }[/math] можно убрать и использовать формулу для произвольных частот. При подстановке [math]\displaystyle{ \alpha(\omega) }[/math] в исходную формулу для [math]\displaystyle{ u(\omega) }[/math] получается формула Планка. Таким образом, важным следствием справедливости формулы Планка является существование вынужденных переходов, которые необходимы для реализации лазерной генерации.

Связь с другими формулами

Закон Рэлея — Джинса

Синим и чёрным цветами обозначены спектры, соответствующие закону Планка и закону Рэлея — Джинса при одной температуре. Видно, что во втором случае наблюдается неограниченный рост мощности при уменьшении длины волны

Закон Рэлея — Джинса — приближение закона Планка, хорошо работающее при [math]\displaystyle{ h c \ll \lambda kT }[/math] (то есть в диапазоне больших длин волн и малых частот), но сильно расходящееся с ним при [math]\displaystyle{ h c }[/math], сравнимых или больших [math]\displaystyle{ \lambda kT }[/math]. В законе Рэлея — Джинса используется приближение [math]\displaystyle{ e^{\frac{hc}{\lambda kT}} \approx 1 + \frac{hc}{\lambda kT} }[/math], справедливое при малых [math]\displaystyle{ \frac{hc}{\lambda kT} }[/math], поэтому приближение выглядит следующим образом:

[math]\displaystyle{ B_\lambda = \frac{2 h c^2}{\lambda^5} \frac{\lambda kT}{hc} = \frac{2ckT}{\lambda^4} }[/math].

В рамках классической физики в результате вывода закона излучения получается именно закон Рэлея — Джинса. Однако при малых длинах волн закон Рэлея — Джинса не только расходится с экспериментом, но и предсказывает неограниченный рост мощности излучения при приближении длины волны к нулю. Этот парадокс получил название ультрафиолетовой катастрофы (см. выше).

Закон излучения Вина

Спектры излучения по закону Планка (зелёный), в приближении Рэлея — Джинса (красный) и в приближении Вина (синий). Оси имеют логарифмический масштаб; температура тела — 0,008 К

Закон излучения Вина — приближение закона Планка, хорошо работающее при [math]\displaystyle{ h c \gg \lambda kT }[/math] — в области малых длин волн и больших частот. Закон излучения Вина предполагает, что при [math]\displaystyle{ h c \gg \lambda kT }[/math] единицей в знаменателе формулы Планка можно пренебречь и считать [math]\displaystyle{ e^{\frac{hc}{\lambda kT}} - 1 \approx e^{\frac{hc}{\lambda kT}} }[/math]. Тогда формула принимает вид:

[math]\displaystyle{ B_\lambda = \frac{2 h c^2}{\lambda^5} e^{-\frac{hc}{\lambda kT}} }[/math].

Закон Стефана — Больцмана

Плотность потока энергии соответствует площади под графиком функции. По закону Стефана — Больцмана она пропорциональна четвёртой степени температуры

Закон Стефана — Больцмана — выражение, описывающее излучение абсолютно чёрного тела во всём электромагнитном диапазоне. Оно выводится из закона Планка интегрированием по частоте или, в зависимости от формы записи, по длине волны:

[math]\displaystyle{ B(T) = \int_0^\infty{B_\nu} d\nu = \int_0^\infty{B_\lambda} d\lambda }[/math],

[math]\displaystyle{ B(T) = \frac{2h}{c^2} \int_0^\infty \frac{\nu^3 d \nu}{e^{\frac{h\nu}{kT}} - 1} }[/math].

Заменим [math]\displaystyle{ x = \frac{h\nu}{kT} }[/math], тогда [math]\displaystyle{ d\nu = \frac{kT}{h}dx }[/math]:

[math]\displaystyle{ B(T) = \frac{2h}{c^2} \frac{k^4}{h^4} T^4 \int_0^\infty \frac{x^3 d x}{e^x - 1} }[/math].

Этот определённый интеграл равен [math]\displaystyle{ \frac{\pi^4}{15} }[/math]. Можно выразить [math]\displaystyle{ B(T) = AT^4 }[/math], где [math]\displaystyle{ A }[/math] — константа:

[math]\displaystyle{ A = \frac{2 k^4}{c^2 h^3} \frac{\pi^4}{15} }[/math].

Плотность потока энергии при этом в [math]\displaystyle{ \pi }[/math] раз больше энергетической яркости, поэтому для вычисления первой используется коэффициент [math]\displaystyle{ \sigma = \pi A }[/math], называемый постоянной Стефана — Больцмана, равный 5,67⋅10⁻⁸ Вт·м⁻²·K⁻⁴. Мощность излучения с единичной площади [math]\displaystyle{ F }[/math] в таком случае может быть выражена как [math]\displaystyle{ F = \sigma T^4 }[/math]. Это выражение и называется законом Стефана — Больцмана.

Закон смещения Вина

По закону смещения Вина длина волны, на которой достигается максимальная излучательная способность, обратно пропорциональна температуре

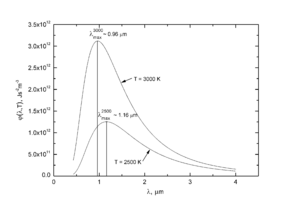
Закон смещения Вина связывает длину волны, на которой излучательная способность абсолютно чёрного тела максимальна, с его температурой. Он выводится из закона Планка дифференцированием его по частоте или длине волны, в зависимости от формы записи, и приравниванием производной к нулю, который достигается в максимуме функции. При этом получается соотношение [math]\displaystyle{ \lambda_{max}T = b }[/math], где [math]\displaystyle{ b }[/math] — константа, равная 0,0029 м·K. Таким образом, при увеличении температуры длина волны максимума уменьшается.

Хотя для частот можно проделать аналогичную процедуру, частоту максимума спектральной плотности нельзя рассчитать по формуле [math]\displaystyle{ \nu_{max} = \frac{c}{\lambda_{max}} }[/math], так как связь между частотой и длиной волны нелинейна, а излучательная способность рассчитывается по излучению на единичном интервале частот или длин волн.

Применение

Для абсолютно чёрного тела спектр описываемый законом Планка однозначно связан с его температурой. Поэтому закон находит применение в пирометрии, то есть дистанционном определении температуры горячих тел. В случае отличия спектра тела от излучения абсолютно чёрного тела пирометр измеряет эффективную температуру, которая называется радиационной [math]\displaystyle{ T_r }[/math]. Зная отношение испускательной способности исследуемого тела к испускательной способности абсолютно чёрного тела [math]\displaystyle{ Q_T=E_T/\varepsilon_T\lt 1 }[/math], которая показывает отличие от формулы Планка, можно найти реальную температуру [math]\displaystyle{ T=T_r/(Q_T)^{1/4} }[/math]. Для многих практических важных материалов значения [math]\displaystyle{ Q_T }[/math] известны.

Литература

• Кононович Э. В.; Мороз В. И. Общий курс астрономии / Под ред. В. В. Иванова. — 2-е, испр. — М.: Едиториал УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
• Сивухин Д. В. Общий курс физики. — М.: Физматлит МФТИ, 2002. — Т. 4. Оптика. — 792 с. — ISBN 5-9221-0228-1.
• Джеммер М. Эволюция понятий квантовой механики. — М.: Наука, 1985. — 384 с.
• Ельяшевич М. А. Планка закон излучения // Физическая энциклопедия. — М.: БРЭ, 1992. — Т. 3. — С. 625—626.
• Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 5th Edition. — Berlin: Springer, 2007. — 510 p. — ISBN 978-3-540-34143-7.
• Ландсберг Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот.. — М.: Физматлит, 2003. — 848 с. — ISBN 5-9221-0314-8.