Тензорное произведение

Тензорное произведение — операция над векторными пространствами, а также над элементами (векторами, матрицами, операторами, тензорами и т. д.) перемножаемых пространств.

Тензорное произведение линейных пространств [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] есть линейное пространство, обозначаемое [math]\displaystyle{ A \otimes B }[/math]. Для элементов [math]\displaystyle{ a \in A }[/math] и [math]\displaystyle{ b \in B }[/math] их тензорное произведение [math]\displaystyle{ a \otimes b }[/math] лежит в пространстве [math]\displaystyle{ A \otimes B }[/math].

Обозначение тензорного произведения произошло по аналогии с обозначением для декартова произведения множеств.

Тензорное произведение линейных (векторных) пространств

Конечномерные пространства

Пусть [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] — конечномерные векторные пространства над полем [math]\displaystyle{ K }[/math], [math]\displaystyle{ \{ e_i \}_{i=1\dots n} }[/math] — базис в [math]\displaystyle{ A }[/math], [math]\displaystyle{ \{ f_k \}_{k=1\dots m} }[/math] — базис в [math]\displaystyle{ B }[/math]. Тензорным произведением [math]\displaystyle{ A \otimes B }[/math] пространств [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] будем называть векторное пространство, порождённое элементами [math]\displaystyle{ e_i \otimes f_k }[/math], называемыми тензорными произведениями базисных векторов. Тензорное произведение [math]\displaystyle{ a \otimes b }[/math] произвольных векторов [math]\displaystyle{ a \in A,~b\in B }[/math] можно определить, полагая операцию [math]\displaystyle{ \otimes }[/math] билинейной:

[math]\displaystyle{ (\lambda a_1 + \mu a_2) \otimes b = \lambda\, a_1 \otimes b + \mu\, a_2 \otimes b,~~\lambda,\mu \in K }[/math]

[math]\displaystyle{ a \otimes (\lambda b_1 + \mu b_2) = \lambda\, a \otimes b_1 + \mu\, a \otimes b_2,~~\lambda,\mu \in K }[/math]

При этом тензорное произведение произвольных векторов [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] выражается как линейная комбинация базисных векторов [math]\displaystyle{ e_i \otimes f_k }[/math]. Элементы в [math]\displaystyle{ A \otimes B }[/math], представимые в виде [math]\displaystyle{ a \otimes b }[/math], называются разложимыми.

Хотя тензорное произведение пространств определяется через выбор базисов, его геометрические свойства не зависят от этого выбора.

Определение с помощью универсального свойства

Тензорное произведение — это в некотором смысле наиболее общее пространство, в которое можно билинейно отобразить исходные пространства. А именно, для любого другого пространства [math]\displaystyle{ C }[/math] и билинейного отображения [math]\displaystyle{ \otimes^\prime: A \times B \to C }[/math] существует единственное линейное отображение [math]\displaystyle{ f: A \otimes B \to C }[/math] такое, что

[math]\displaystyle{ \otimes^\prime = f \circ \otimes , }[/math]

где [math]\displaystyle{ \circ }[/math] обозначает композицию функций.

В частности, отсюда следует, что тензорное произведение не зависит от выбора базисов в [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math], так как все удовлетворяющие универсальному свойству пространства [math]\displaystyle{ A \otimes B }[/math] оказываются канонически изоморфны.

Таким образом, задание произвольного билинейного отображения [math]\displaystyle{ L^2 \ni \varphi: A \times B \to C }[/math] эквивалентно заданию линейного отображения [math]\displaystyle{ L \ni \varphi: A \otimes B \to C }[/math]: пространства [math]\displaystyle{ \ L^2(A \times B, C) }[/math] и [math]\displaystyle{ L(A\otimes B, C) }[/math] являются канонически изоморфными.

Произведение более чем двух пространств

Приведенное универсальное свойство может быть продолжено на произведения более чем двух пространств. Например, пусть [math]\displaystyle{ V_1 }[/math], [math]\displaystyle{ V_2 }[/math], и [math]\displaystyle{ V_3 }[/math] — три векторных пространства. Тензорное произведение [math]\displaystyle{ V_1\otimes V_2\otimes V_3 }[/math] вместе с трилинейным отображением из прямого произведения

[math]\displaystyle{ \varphi:V_1\times V_2\times V_3 \to V_1\otimes V_2\otimes V_3 }[/math]

имеет такой вид, что любое трилинейное отображение [math]\displaystyle{ F }[/math] из прямого произведения в векторное пространство [math]\displaystyle{ W }[/math]

[math]\displaystyle{ F:V_1\times V_2\times V_3\to W }[/math]

единственным образом пропускается через тензорное произведение:

[math]\displaystyle{ F=L\circ\varphi }[/math]

где [math]\displaystyle{ L }[/math] — линейное отображение. Тензорное произведение характеризуется этим свойством однозначно, с точностью до изоморфизма. Результат приведенной конструкции совпадает с повторением тензорного произведения двух пространств. Например, если [math]\displaystyle{ V_1 }[/math], [math]\displaystyle{ V_2 }[/math] и [math]\displaystyle{ V_3 }[/math] — три векторных пространства, то существует (естественный) изоморфизм

[math]\displaystyle{ V_1\otimes V_2\otimes V_3\cong V_1\otimes(V_2\otimes V_3)\cong(V_1\otimes V_2)\otimes V_3. }[/math]

В общем случае тензорное произведение произвольного индексированного семейства множеств [math]\displaystyle{ V_i }[/math], [math]\displaystyle{ i\in I }[/math] определяется как универсальный объект для полилинейных отображений из прямого произведения [math]\displaystyle{ \textstyle\prod_{i\in I} V_i }[/math].

Пусть [math]\displaystyle{ n }[/math] — произвольное натуральное число. Тогда [math]\displaystyle{ n }[/math]-й тензорной степенью пространства [math]\displaystyle{ V }[/math] называется тензорное произведение [math]\displaystyle{ n }[/math] копий [math]\displaystyle{ V }[/math]:

[math]\displaystyle{ V^{\otimes n} \;\overset{\mathrm{def}}{=}\; \underbrace{V\otimes\cdots\otimes V}_{n}. }[/math]

Функториальность

Тензорное произведение действует также на линейных отображениях. Пусть [math]\displaystyle{ A\colon U_1 \to U_2 }[/math], [math]\displaystyle{ B\colon W_1 \to W_2 }[/math] — линейные операторы. Тензорное произведение операторов [math]\displaystyle{ A\otimes B\colon U_1\otimes W_1 \to U_2\otimes W_2 }[/math] определяется по правилу

[math]\displaystyle{ (A\otimes B)(u\otimes w) = (A u)\otimes (B w),~~ u\in U_1,\,w\in W_1 }[/math]

После этого определения тензорное произведение становится бифунктором из категории векторных пространств в себя, ковариантным по обоим аргументам.

Если матрицы операторов A и B при некотором выборе базисов имеют вид

[math]\displaystyle{ \mathrm{A} = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix} }[/math]

[math]\displaystyle{ \mathrm{B} = \begin{bmatrix} b_{11} & \cdots & b_{1q} \\ \vdots & \ddots & \vdots \\ b_{p1} & \cdots & b_{pq} \end{bmatrix} }[/math]

то матрица их тензорного произведения запишется в базисе, образованном тензорным произведением базисов, в виде блочной матрицы

[math]\displaystyle{ \mathrm{A} \otimes \mathrm{B} = \begin{bmatrix} a_{11} B & \cdots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1} B & \cdots & a_{mn} B \end{bmatrix} = }[/math]

[math]\displaystyle{ = \begin{bmatrix} a_{11} b_{11} & a_{11} b_{12} & \cdots & a_{11} b_{1q} & \cdots & \cdots & a_{1n} b_{11} & a_{1n} b_{12} & \cdots & a_{1n} b_{1q} \\ a_{11} b_{21} & a_{11} b_{22} & \cdots & a_{11} b_{2q} & \cdots & \cdots & a_{1n} b_{21} & a_{1n} b_{22} & \cdots & a_{1n} b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{11} b_{p1} & a_{11} b_{p2} & \cdots & a_{11} b_{pq} & \cdots & \cdots & a_{1n} b_{p1} & a_{1n} b_{p2} & \cdots & a_{1n} b_{pq} \\ \vdots & \vdots & & \vdots & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \vdots & & \vdots & & \ddots & \vdots & \vdots & & \vdots \\ a_{m1} b_{11} & a_{m1} b_{12} & \cdots & a_{m1} b_{1q} & \cdots & \cdots & a_{mn} b_{11} & a_{mn} b_{12} & \cdots & a_{mn} b_{1q} \\ a_{m1} b_{21} & a_{m1} b_{22} & \cdots & a_{m1} b_{2q} & \cdots & \cdots & a_{mn} b_{21} & a_{mn} b_{22} & \cdots & a_{mn} b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{p1} & a_{m1} b_{p2} & \cdots & a_{m1} b_{pq} & \cdots & \cdots & a_{mn} b_{p1} & a_{mn} b_{p2} & \cdots & a_{mn} b_{pq} \end{bmatrix} }[/math]

Соответствующая операция над матрицами называется кронекеровским произведением, по имени Леопольда Кронекера.

Частные случаи

Тензорное произведение двух векторов

(Матричное) умножение вектора-столбца справа на вектор-строку описывет их тензорное произведение:

[math]\displaystyle{ \mathbf{a} \otimes \mathbf{b} \leftrightarrow \begin{bmatrix}a_1 \\ a_2 \\ a_3 \\ a_4\end{bmatrix} \begin{bmatrix}b_1 & b_2 & b_3\end{bmatrix} = \begin{bmatrix}a_1b_1 & a_1b_2 & a_1b_3 \\ a_2b_1 & a_2b_2 & a_2b_3 \\ a_3b_1 & a_3b_2 & a_3b_3 \\ a_4b_1 & a_4b_2 & a_4b_3\end{bmatrix}. }[/math]

Свойства

• [math]\displaystyle{ \dim A\otimes B = \dim A \cdot \dim B }[/math]

Следующие алгебраические свойства основаны на каноническом изоморфизме:

• Ассоциативность

[math]\displaystyle{ (A \otimes B)\otimes C \simeq A \otimes(B \otimes C) }[/math]

• Формально говоря, тензорное произведение не коммутативно, но существует естественный изоморфизм [math]\displaystyle{ A \otimes B \to B \otimes A }[/math]
• Линейность

[math]\displaystyle{ A \otimes (B \oplus C) \simeq (A\otimes B) \oplus (A \otimes C) }[/math]

[math]\displaystyle{ \oplus }[/math] — внешняя сумма линейных пространств.

Тензорное произведение модулей

Пусть [math]\displaystyle{ A_1,A_2,\dots,A_n }[/math] — модули над некоторым коммутативным кольцом [math]\displaystyle{ R }[/math]. Тензорным произведением модулей называется модуль [math]\displaystyle{ B }[/math] над [math]\displaystyle{ R }[/math], данный вместе с полилинейным отображением [math]\displaystyle{ f\colon A_1\times \dots \times A_n \to B }[/math] и обладающий свойством универсальности, то есть такой, что для всякого модуля [math]\displaystyle{ C }[/math] над [math]\displaystyle{ R }[/math] и любого полилинейного отображения [math]\displaystyle{ g\colon A_1\times \dots \times A_n \to C }[/math] существует единственный гомоморфизм модулей [math]\displaystyle{ h\colon B \to C }[/math] такой, что диаграмма

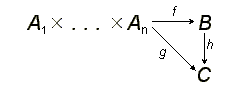
коммутативна. Тензорное произведение обозначается [math]\displaystyle{ A_1 \otimes\ldots\otimes A_n }[/math]. Из универсальности тензорного произведения следует, что оно определено однозначно с точностью до изоморфизма.

Для доказательства существования тензорного произведения любых модулей над коммутативным кольцом построим свободный модуль [math]\displaystyle{ M }[/math], образующими которого будут n-ки элементов модулей [math]\displaystyle{ (x_1,\dots,x_n) }[/math] где [math]\displaystyle{ x_i \in A_i }[/math]. Пусть [math]\displaystyle{ N }[/math] — подмодуль [math]\displaystyle{ M }[/math], порождаемый следующими элементами:

1. [math]\displaystyle{ (x_1,\dots,x_i + y_i,\dots,x_n) - (x_1,\dots,x_i,\dots,x_n) - (x_1,\dots,y_i,\dots,x_n) }[/math]
2. [math]\displaystyle{ (x_1,\dots,\lambda x_i,\dots,x_n) - \lambda(x_1,\dots,x_i,\dots,x_n) }[/math]

Тензорное произведение определяется как фактормодуль [math]\displaystyle{ B=M/N }[/math], класс [math]\displaystyle{ (x_1,\dots,x_n) + N }[/math] обозначается [math]\displaystyle{ x_1 \otimes \dots \otimes x_n }[/math], и называется тензорным произведением элементов [math]\displaystyle{ x_i }[/math], a [math]\displaystyle{ f }[/math] определяется как соответствующее индуцированное отображение.

Из 1) и 2) следует что отображение [math]\displaystyle{ f\colon A_1\times \dots \times A_n \to B }[/math] полилинейно. Докажем, что для любого модуля [math]\displaystyle{ C }[/math] и любого полилинейного отображения [math]\displaystyle{ g\colon A_1\times \dots \times A_n \to C }[/math] существует единственный гомоморфизм модулей [math]\displaystyle{ h }[/math], такой, что [math]\displaystyle{ g = h \circ f }[/math].

В самом деле, так как [math]\displaystyle{ M }[/math] свободен, то существует единственное отображение [math]\displaystyle{ h^* }[/math], делающее диаграмму

коммутативной, а в силу того, что [math]\displaystyle{ g }[/math] полилинейно, то на [math]\displaystyle{ N }[/math] [math]\displaystyle{ h^*(N) = 0 }[/math], отсюда, переходя к индуцированному отображению, получаем, что [math]\displaystyle{ h\colon M/N \to C }[/math], будет тем самым единственным гомоморфизмом, существование которого и требовалось доказать.

Элементы [math]\displaystyle{ A_1 \otimes \dots \otimes A_n }[/math], представимые в виде [math]\displaystyle{ x_1 \otimes \dots \otimes x_n }[/math], называются разложимыми.

Если [math]\displaystyle{ f_i\colon A_i \to B_i }[/math] — изоморфизмы модулей, то индуцированный гомоморфизм, соответствующий билинейному отображению

[math]\displaystyle{ f_1\otimes\dots\otimes f_n\colon A_1\otimes\dots\otimes A_n \to B_1\otimes\dots\otimes B_n }[/math]

существующий по свойству универсальности, называется тензорным произведением гомоморфизмов [math]\displaystyle{ f_i }[/math].

Особенно простой случай получается в случае свободных модулей. Пусть [math]\displaystyle{ e_{i 1},\dots,e_{i n} }[/math] — базис модуля [math]\displaystyle{ A_i }[/math]. Построим свободный модуль [math]\displaystyle{ F }[/math] над нашим кольцом, имеющий в качестве базиса элементы, соответствующие n-кам [math]\displaystyle{ (e_{1 m}, e_{2 p}, \dots, e_{n s}) }[/math], определив отображение [math]\displaystyle{ f(e_{1 m}, e_{2 p}, \dots, e_{n s}) \to (e_{1 m}, e_{2 p}, \dots, e_{n s}) }[/math] и распространив его на [math]\displaystyle{ A_1 \times \dots \times A_n }[/math] по линейности. Тогда [math]\displaystyle{ F }[/math] является тензорным произведением, где [math]\displaystyle{ (e_{1 m}, e_{2 p}, \dots, e_{n s}) }[/math] является тензорным произведением элементов [math]\displaystyle{ e_{1m} \otimes e_{2p} \otimes \dots\otimes e_{ns} }[/math]. Если число модулей и все их базисы конечны, то

[math]\displaystyle{ \mathrm{rank} (A_1 \otimes \dots \otimes A_n) = \mathrm{rank}\, A_1 \cdot \dots \cdot \mathrm{rank}\, A_n }[/math].

Литература

• Винберг Э. Б. Курс алгебры. — 3-е изд. — М.: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7.
• Ленг С. Алгебра. — М.: Мир, 1967.
• Ван дер Варден Б. Л. Алгебра. — М.: Наука, 1976. — 648 с.

См. также

• Свёртка тензора
• Тензор
• Тензорное поле
• Тензорная алгебра
• Тензорное произведение графов