Диаграммы Фейнмана

Диаграмма Фейнмана — графическое представление математических уравнений, описывающих взаимодействия субатомных частиц в рамках квантовой теории поля. Этот инструмент изобрёл американский физик Ричард Фейнман в конце 1940-х годов, во время его работы в Корнельском университете, для выполнения расчётов рассеяния частиц.
Взаимодействие между субатомными частицами требует сложных вычислений, которые трудно понять интуитивно. Диаграммы Фейнмана обеспечивают простую систему визуализации для упрощения этих формул. Эта система произвела революцию во всей теоретической физике, затем её применили в прикладной физике.
Вычисления амплитуды вероятности выполняются с использованием интегралов в комплексной плоскости от большого количества переменных. Эти конкретные интегралы имеют регулярную структуру, которая позволяет представлять их в виде наборов диаграмм. Диаграмма Фейнмана представляет вклад траекторий частиц, которые соединяются, а затем разделяются на этой диаграмме. Технически — это графическое представление математического слагаемого в ряду теории возмущений.
Несмотря на свой внешний вид, диаграммы Фейнмана не отображают физических явлений. Единственными реальными элементами являются частицы, входящие и исходящие линии графа, а не взаимодействия, учитываемые диаграммой.
История

Диаграммы Фейнмана произвели революцию в физике элементарных частиц, сделав доступными вычисления посредством простых рисунков и абстрактных концепций[2]. Диаграммы позже использовалась в ядерной физике, в теории гравитации или в физике твёрдого тела: они получили распространение в многих областях физики[3]. Джулиан Швингер сравнил их с появлением компьютера[4][Note 1]:
точно так же, как микрочип последних лет, диаграмма Фейнмана демократизировала вычисления.
Их значимость такова, что историки науки отнесли их к определённой категории: Эндрю Уорвик придумал термин «теоретическая технология», и Урсула Клейн[англ.] — «бумажные инструменты»[5].
Фейнман изобрёл диаграммную технику для выполнения расчётов дисперсии в квантовой электродинамике. Чтобы упростить свои вычисления амплитуд вероятностей, он связал математические термины с графиками, представляющими частицы линиями, а их взаимодействия — вершинами, пересечением этих линий[6]. Его первой идеей было создание системы обозначений, позволяющей ему производить громоздкие вычисления, необходимые в квантовой электродинамике[7]. Когда он представил их весной 1948 года, вряд ли кто-либо из физиков осознал их значение[Note 2]. Но в последующие месяцы каждый принял их со своими собственными условностями. Несмотря на начало стандартизации в 1949 году, были разработаны и другие семейства диаграмм для различных целей, заменив существующие инструменты[8].
В течение первых шести лет диаграммы распространились среди около сотни физиков из уст в уста и в научных статьях; первые книги на английском языке по этой теме появились в 1955 году[Note 3][9]. Они распространились в основном благодаря работе Фримена Дайсона, который прибыл в Корнелл в 1947 году для работы с Гансом Бете. Коллега Фейнмана много обсуждал с ним этот графический метод, облегчающий вычисления перенормировок. Он также изучил чисто алгебраический метод Джулиана Швингера, а также методы Синъитиро Томонаги и, наконец, продемонстрировал, что эти три подхода эквивалентны, создав, кроме того, руководство по применению диаграмм Фейнмана, в то время как последний ещё не опубликовал статью по этой теме[10].
До Фейнмана несколько ранее используемых графических представлений для более интуитивного понимания концепций квантовой механики были далеко не такими полными. В частности, использовалась диаграмма переходов между энергетическими уровнями (вдохновлённая диаграммами спектроскопии) и диаграмма, придуманная Грегором Вентцелем для описания процессов обмена между частицами[Note 4][11]. Фейнмана также вдохновили диаграммы Минковского, используемые в специальной теории относительности[12].
Описание

Диаграммы Фейнмана — это графические представления слагаемых, используемых в пертурбативных вычислениях. Несмотря на то, что они никогда не были стандартизированы, существует множество соглашений, в частности потому, что они имеют очень разные приложения, помимо описания взаимодействия между частицами[13]. По своей природе в квантовой физике они представляют собой элегантный способ перейти от описания процесса взаимодействия электронов и фотонов к математической формуле, которая задаёт его амплитуду вероятности[14]. Со временем диаграммы стали языком, на котором физики могут рассказывать о своих расчётах[15].
Эти диаграммы, которые, по всей видимости, визуально представляют взаимодействия между частицами, на самом деле являются мощным математическим инструментом. Ричард Фейнман создал их для выполнения вычислений в квантовой электродинамике[3]. Затем они были обобщены на все взаимодействия, в которых участвуют известные элементарные частицы, то есть на электромагнитное, сильное и слабое взаимодействия. Фермионы представлены линией со стрелками, антифермионы — линией со стрелкой в противоположном направлении, калибровочные бозоны имеют различные изображения: фотон — волнистой линией, глюон — закольцованной линией, бозоны W, Z и Хиггса — пунктирной линией, сопровождаемой символами частиц (W+, W-, Z, H); бозоны переносчики слабого взаимодействия (W+, W-, Z) иногда изображаются той же волнистой линией, что и фотон[16].
- Элементарные частицы
-
фермион -
антифермион -
фотон -
глюон -
массивный бозон
Примеры диаграмм где используется нескольких типов частиц.
- Наиболее вероятные реакции рождения бозона Хиггса[17]
-
-
-
-
Духи Фадеева — Попова нарисованы линией из точек[18].
- Вершина антидух-дух-глюон
-
Представление других частиц
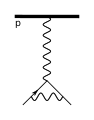
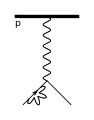
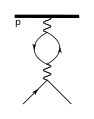
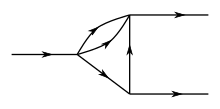
Поскольку диаграммы Фейнмана не стандартизированы даже для элементарных взаимодействий, некоторые из них могут иметь очень разные представления, часто адаптированные к используемому контексту. Протон, который представляет собой составную частицу, может отображаться в виде линии со стрелкой, сопровождаемой буквой [math]\displaystyle{ p }[/math], круг, который в более общем виде представляет адроны[19], или три параллельные линии, изображающие два u-кварка и один d-кварк[20][21][22].
- Адронные представления
-
Атом водорода (протон и электрон).
-
Кварк-антикварковая аннигиляция из двух адронов.
-
Бета-распад нейтрона на протон.
-
Ещё одна форма бета-распада.
Условные обозначения
Световое или электронное явление, представленное на диаграмме Фейнмана, называется «последовательность»[23]. Последовательности происходят в пространстве-времени, изображающемся в системе отсчета с пространством по оси абсцисс, упрощённым до одного измерения вместо трёх, и временем по ординате[24]. Фейнман предпочёл направить время вверх, этот выбор был чисто произвольным, но физики элементарных частиц, похоже, все больше предпочитают ориентацию слева направо[Note 5][12][25].
- Соглашения о пространстве и времени
-
Время направлено вверх — соглашение Фейнмана -
Время направлено направо — общепринятое соглашение
Фермионы представлены прямой линией со стрелкой, а частицы, переносчики взаимодействий (бозоны), — волнистой или пунктирной линиями. Последовательность испускания или поглощения фотона называется «соединение» или «связь»; она представлена вершиной — точкой соединения линий[26]. Связь называет излучение или поглощение по-разному, потому что оба явления имеют одинаковую амплитуду, равную постоянной тонкой структуры [math]\displaystyle{ \alpha }[/math] для квантовой электродинамики[1] или константе связи сильного ядерного взаимодействия [math]\displaystyle{ \alpha_s }[/math] для квантовой хромодинамики[27].
Схема построена из трёх элементов: вершины, в которых сохраняются энергия и импульс, внешние линии представляют входящие и исходящие реальные частицы, а внутренние линии обозначают виртуальные частицы[15]. С каждой линией или вершиной связан множитель, который вносит вклад в амплитуду вероятности описанного процесса, фактор, связанный с виртуальной частицей (внутренней линией), называется пропагатором[28].
Свойства

Взаимодействие описывается набором диаграмм Фейнмана и определяется входящими (начальными) и исходящими (конечными) частицами. Можно измерить свойства этих частиц, такие как их энергия или их импульс, и убедиться, что они соответствуют уравнению эквивалентности массы и энергии Эйнштейна,
- [math]\displaystyle{ E^2 - p^2c^2 = m^2 c^4\, }[/math]
в его релятивистской версии (сохранение 4-импульса)[29]. Говорят, что наблюдаемые таким образом частицы находятся на массовой поверхности[30][31].
С другой стороны, все линии, что находятся посередине, не поддаются измерению: они обозначают виртуальные частицы, которые не подчиняются соотношению эквивалентности массы и энергии, и не ограничены скоростью света, а также не обязаны следовать по стреле времени. Говорят, что они находятся вне массовой поверхности[32][31].
Чтобы проанализировать физический процесс, входящие и выходящие частицы которого известны, диаграммы Фейнмана позволяют представить бесконечное количество возможных процессов, которые происходят между этими внешними линиями. Каждая диаграмма соответствует, благодаря правилам Фейнмана, комплексному числу[Note 6], а сумма всех этих чисел с точностью до множителя равна амплитуде рассеяния реакции[31]. Эффективность этого метода заключается в том, что каждая вершина связана с коэффициентом, пропорциональным константе связи, которая имеет очень маленькое значение. Например, в квантовой электродинамике стоит постоянная тонкой структуры[1]:
- [math]\displaystyle{ \alpha = \frac{e^2}{\hbar c} \approx \frac{1}{137}\,. }[/math]
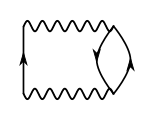
Поскольку множители диаграммы умножаются, для получения её амплитуды, все диаграммы с большим количеством вершин имеют незначительный вклад; поэтому диаграммы с более чем четырьмя вершинами в квантовой электродинамике[31] используются редко, поскольку получается хорошее приближение с шестью значащими цифрами[33].
- Примеры четырёхвершинных диаграмм
-
-
-
-
Данные процессы включающие четыре вершины имеют одну петлю, поэтому называются однопетлевыми. Диаграммы без петель называются древесными. Если в диаграмме используется n петель, то соответствующая диаграмма называется n-петлевой. Петлевые диаграммы описывают радиационные поправки, которые исчезают в классическом пределе при [math]\displaystyle{ \hbar\rightarrow 0\, }[/math][31].

В особых случаях необходимо повысить точность вычислений до более высоких порядков. Например, в 2012 году, чтобы вычислить значение постоянной тонкой структуры, группа физиков использовала измеренный ранее аномальный магнитный момент электрона для сравнения с теоретическим расчётом в десятом порядке теории возмущений, включающим 12672 диаграмм Фейнмана. Полученная ошибка для оценки постоянной тонкой структуры составила менее одной миллиардной доли[34].
Фундаментальные взаимодействия
Диаграммы Фейнмана используются для описания трёх фундаментальных взаимодействий, помимо гравитации.
Квантовая электродинамика

В этой теории три основных правила позволяют генерировать все физические явления, которые связаны со светом и электронами[23]:
- фотон переходит из одной точки в другую;
- электрон переходит из одной точки в другую;
- электрон испускает или поглощает фотон.
В более общем подходе квантовая электродинамика имеет дело с взаимодействиями между заряженными частицами (включая электроны и их античастицы — позитроны) и электромагнитным полем (векторами сил которого являются фотоны); на диаграммах Фейнмана электрон представлен стрелкой, направленной по оси времени, позитрон — стрелкой, направленной в противоположном направлении, а фотон — волнистой линией[Note 7][35][36].
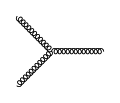
Взаимодействия между этими тремя частицами сводятся к единому узору при вершине, состоящему из входящей стрелки, исходящей стрелки и связи с фотоном. В зависимости от ориентации этой вершины во времени получается шесть возможных взаимодействий[37][15].
-
Электрон излучает фотон : [math]\displaystyle{ e^- \to e^- + \gamma }[/math]
-
Электрон поглощает фотон : [math]\displaystyle{ e^- + \gamma \to e^- }[/math]
-
Позитрон излучает фотон : [math]\displaystyle{ e^+ \to e^+ + \gamma }[/math]
-
Позитрон поглощает фотон : [math]\displaystyle{ e^+ + \gamma \to e^+ }[/math]
-
Позитрон и электрон аннигилируют в фотоне : [math]\displaystyle{ e^+ + e^- \to \gamma }[/math]
-
Фотон создает электрон и позитрон : [math]\displaystyle{ \gamma \to e^- + e^+ }[/math]
Все взаимодействия между заряженными частицами и светом строятся из этих основных кирпичиков, и только их, потому что они подчиняются законам сохранения, в частности, сохранению энергии, сохранению импульса и сохранению электрического заряда. Любое более сложное взаимодействие — это комбинация этих шести вершин[38].
Квантовая хромодинамика
В 1968 году Ричард Фейнман показал, что его диаграммы также можно применить к сильному взаимодействию, поэтому они позволяют описывать квантовую хромодинамику, добавляя новые правила. Таким образом, фундаментальным процессом, аналогичным электрон-фотонной реакции в электродинамике, является кварк-глюонная реакция, в которой сохраняется цветовой заряд (но не аромат). У глюонов, несущих подобно кваркам цветовые заряды (в отличие от фотонов, которые являются нейтральными), есть вершины, содержащие только глюоны[39].
- Вершина квантовой хромодинамики
-
Вершина кварк глюон КХД
-
Вершина 3 глюона КХД
-
Вершина 4 глюона КХД
Изучение сильных взаимодействий с диаграммами Фейнмана возможно благодаря свойству асимптотической свободы, которое позволяет применять теорию возмущений к кваркам и глюонам: на очень коротком расстоянии это взаимодействие становится слабым[40][41]. Затем определяется константа связи сильного взаимодействия для вершины, отмечено как [math]\displaystyle{ \alpha_s }[/math] — это эквивалент постоянной тонкой структуры в квантовой электродинамике. Сложность квантовой хромодинамики связана с тем, что на кварки сильно влияют непертурбативные силы. Фиксируя на очень больших уровнях импульсов, где связь слабая, значение [math]\displaystyle{ \alpha_s }[/math] позволяет рассчитать результат процесса рассеяния при высоких энергиях[42].
Слабое взаимодействие
В слабом взаимодействии участвуют три его калибровочных бозона, W-бозон в двух его состояниях, [math]\displaystyle{ W^+ }[/math] и [math]\displaystyle{ W^- }[/math], а также бозон [math]\displaystyle{ Z^0 }[/math][43]. Эти переносчики обычно изображаются пунктирной или волнистой линией (такой же, как у фотона) с буквой соответствующего бозона. Прямая линия со стрелками продолжается здесь до кварков и других лептонов, с соответствующими им символами[44].
- Вершина электрослабого взаимодействия (без символов)
-
-
-
-
-
-
Значение
Диаграммы Фейнмана не являются представлением траектории частиц. Математически они представляют собой графический способ отображения содержания теоремы Вика[45][46]. Действительно, при каноническом квантовании оценке квантовой теории поля диаграмма соответствует члену разложения Вика в теории возмущений для эволюции матрицы рассеяния[47].
Расчёт амплитуды в теории возмущений
Ни один метод не позволяет вычислить точные решения уравнений, задающих состояние квантовой системы, поэтому необходимо прибегать к приближениям, называемым рядами теории возмущений. Диаграммы Фейнмана позволяют визуализировать и легко систематизировать члены этих рядов[48].
Теория позволяет предсказывать значения сечений рассеяния процессов; эти значения сравниваются с результатами экспериментов по физике элементарных частиц, чтобы оценить надёжность данной теоретической модели. Обычно используется дифференциал этого эффективного сечения, который является функцией квадрата модуля амплитуды рассеяния, обозначаемого как [math]\displaystyle{ \mathcal{M} }[/math]:
- [math]\displaystyle{ \mathrm{d} \sigma = \frac{1}{E^2} \, |\mathcal{M}|^2 \mathrm{d} \Omega \,, }[/math]
где [math]\displaystyle{ E }[/math] — предполагаемая равная энергия каждого из двух пучков частиц, участвовавших в эксперименте[49].
Общей формулы для расчёта амплитуды [math]\displaystyle{ \mathcal{M} }[/math] нет, но ряд теории возмущений может приближаться к точному значению[50].
Диаграммы Фейнмана — это графические обозначения членов бесконечного ряда, используемых для выполнения этих вычислений в теории возмущений. Каждая диаграмма представляет собой один из алгебраических членов ряда теории возмущений[51]. Эта алгебраическая сумма, разложение амплитуды рассеяния, эквивалентна серии диаграмм Фейнмана. Таким образом, каждый член связан с графом, который предлагает сценарий поведения в терминах частиц и их взаимодействий, причём каждый сценарий связан с другим своими входящими и исходящими линиями[52]. Переход от одного представления к другому позволяет выполнять вычисления в том виде, что кажется наиболее простым или наиболее подходящим[53].
Одним из первых основных результатов этих диаграмм является то, что они дают графический инструмент для вычисления элементов матрицы рассеяния в любом порядке теории возмущений[54].
Вершина

Заряд электрона [math]\displaystyle{ e }[/math] очень мал — его значение [math]\displaystyle{ e^2 \approx \tfrac{1}{137} }[/math] в правильно подобранных единицах[Note 8]. Когда вычисляется вклад взаимодействия с одиночным фотоном, он пропорционален [math]\displaystyle{ e^2 }[/math], с двумя фотонами — он пропорционален [math]\displaystyle{ e^4 }[/math], с тремя — возникает фактор [math]\displaystyle{ e^6 }[/math], что примерно в 10 000 раз меньше, чем [math]\displaystyle{ e^2 }[/math]. Даже если кажется, что эта идея приводит к очень быстрому устранению вклада незначительных взаимодействий, их практический расчёт чрезвычайно сложен: ученик Вернера Гейзенберга попытался вычислить вклад для двух фотонов (в [math]\displaystyle{ e^4 }[/math]), но в итоге получились сотни слагаемых[1].
В диаграмме Фейнмана вклад пертурбативного члена очевиден: вершина даёт вклад, равный [math]\displaystyle{ e }[/math], тогда все множители можно классифицировать в соответствии с их вкладом, [math]\displaystyle{ e^2 }[/math], [math]\displaystyle{ e^4 }[/math], [math]\displaystyle{ e^6 }[/math] и др.[55]. Чтобы найти вероятность изменения квантового состояния изучаемого явления, остаётся только вычислить те члены, которые необходимы для желаемой точности, исключив бесконечное количество других возможных случаев[56].
Виртуальные частицы
На заре квантовой электродинамики в 1930-х годах расчёты в простейших случаях, таких как знание вероятности рассеяния двух электронов, часто давали бесконечные значения: были возможны только приближения, но как только мы захотели бы найти более точные значения, то возникала бесконечность. Это связано с тем, что виртуальные фотоны, которыми обмениваются заряженные частицы в этом взаимодействии, могут иметь очень высокую энергию, если они используют её в течение очень короткого времени. Помимо неограниченных энергий, количество виртуальных частиц также не ограничено: алгебраические уравнения требуют количества слагаемых, которое растёт экспоненциально с числом фотонов[57].
Вычисление интеграла по путям, который даёт вероятность перехода квантовой частицы из одной точки в другую, требует сложения вкладов всех возможных путей между этими двумя точками, а также учёта вкладов невозможных путей[58]. Точный расчёт невозможен, потому что необходимо было бы суммировать бесконечное количество промежуточных состояний[59]. Диаграммы Фейнмана позволяют найти желаемую вероятность среди этой бесконечности возможностей, причём с помощью чрезвычайно простых правил[60].
Пропагаторы
В диаграммах Фейнмана пропагаторами являются вклады виртуальных частиц. Их название происходит от того факта, что они описывают распространение этих частиц, которые движутся свободно, за исключением точек излучения или поглощения[61]. Ричард Фейнман применил функции Грина к элементарным частицам в форме особого оператора квантовой теории поля, который он назвал пропагатором[62].
Для свободного бозона уравнение Клейна — Гордона даёт уравнение движения:
- [math]\displaystyle{ (p^2 - m^2)\psi(p) = 0\,, }[/math]
где [math]\displaystyle{ \psi(p) }[/math] — скалярная волновая функция. Функция Грина [math]\displaystyle{ G(p) }[/math] является решением следующего уравнения в импульсном пространстве[63]:
- [math]\displaystyle{ (p^2 - m^2)G(p) = \delta^4(p)\,, }[/math]
где символ [math]\displaystyle{ \delta }[/math] обозначает распределение Дирака, с [math]\displaystyle{ \delta^4(p) = \delta(p_0)\delta(p_1)\delta(p_2)\delta(p_3)\,. }[/math]
- [math]\displaystyle{ G(p) = \frac{\delta^4(p)}{p^2 - m^2}\,. }[/math]
Фейнман интерпретировал [math]\displaystyle{ G(p) }[/math] как амплитуду вероятности, связанную с бозоном, распространяющимся с четырёхимпульсом [math]\displaystyle{ p }[/math], что входит в выражение[61]:
- [math]\displaystyle{ \frac{i}{p^2 - m^2}\,. }[/math]
Аналогичным образом он определяет оператор для вершин (отвечающие за испускание или поглощение бозона), что приводит к правилам Фейнмана, позволяющим вычислять амплитуды, описываемые его диаграммами[62].
Представление

Согласно принципу неопределенности Гейзенберга, мы не можем приписать частице траекторию. Нильс Бор интерпретирует его радикально, утверждая, что квантовые явления невозможно представить[6]. Диаграммы Фейнмана, кажется, противоречат этому утверждению, прямо показывая, что может происходить на атомном уровне. Аналогия со следами, оставляемыми частицами в пузырьковых камерах, подкрепляет эту идею[64]. Однако эти диаграммы никоим образом не отображают физические события[65]. Они могут даже вводить в заблуждение, потому что противоречат явлению, которое иллюстрируют: например, в рассеянии Баба электрон и позитрон притягиваются друг к другу, в то время как на их диаграмме линии в конечном итоге раздвигаются, и частицы, кажется, отталкиваются друг от друга[33].
С физической точки зрения диаграмма Фейнмана соответствует бесконечному набору событий, сумме всех возможных и невозможных путей, представленных интегралом по траекториям. Более того, у неё нет масштаба, её вершины и линии не являются ни частицами, ни расстояниями[65]. С математической точки зрения диаграммы, используемые в квантовой теории поля, представляют собой только члены суммы амплитуд вероятностей, аппроксимации в ряде теории возмущений. Такая диаграмма соответствует ненаблюдаемым событиям, называемым «виртуальными частицами»[66].
Ричард Фейнман предостерёг от образного использования его диаграмм. Он рассматривал их только как помощь в интерпретации уравнений теории поля[11]. Он также нашёл их забавными, когда начал их рисовать, и они не были интуитивно понятными, когда он представил их другим физикам[67].
Однако их успех связан с тем, что они оказались ценным подспорьем для визуализации и манипулирования рядами теории возмущений, особенно потому, что каждый алгебраический член имеет соответствующую диаграмму Фейнмана[52]. Таким образом Джулиан Швингер выделил их образовательные и нефизические достоинства[68].
Если максимально упростить, то можно сказать, что диаграммы Фейнмана показывают рассеяние электронов и фотонов в абстрактной форме. Но большинство физиков избегают использования этой аналогии[69] .
Эти диаграммы иногда путают с диаграммами Минковского, существовавшими до фейнмановских и интуитивно описывающими свойства пространства-времени в специальной теории относительности[70].
Правила Фейнмана
Правила Фейнмана переводят диаграмму непосредственно во вклад [math]\displaystyle{ \mathcal{M} }[/math], они ставят в соответствие каждому элементу алгебраический множитель, и произведение этих множителей даёт значение этого вклада (сумма вкладов даёт приблизительное значение [math]\displaystyle{ \mathcal{M} }[/math])[50].
Для последующих алгебраических формул используется система естественных единиц, где приведённая постоянная Планка [math]\displaystyle{ \hbar }[/math] и скорость света [math]\displaystyle{ c }[/math] являются единицами, поэтому: [math]\displaystyle{ \hbar = c = 1 }[/math].
Квантовая электродинамика
Правила Фейнмана для расчета [math]\displaystyle{ -i\mathcal{M} }[/math] в квантовой электродинамике[71]:
| Категория | Символ | Спин | Частица (ы) | Коэффициент умножения |
|---|---|---|---|---|
| Внешние линии | 0 | входящий бозон | 1 | |
| 0 | исходящий бозон | 1 | ||
| 0 | входящий антибозон | 1 | ||
| 0 | исходящий антибозон | 1 | ||
| ½ | входящий фермион | [math]\displaystyle{ u }[/math] | ||
| ½ | уходящий фермион | [math]\displaystyle{ \bar u }[/math] | ||
| ½ | входящий антифермион | [math]\displaystyle{ \bar v }[/math] | ||
| ½ | исходящий антифермион | [math]\displaystyle{ v }[/math] | ||
| 1 | входящий фотон | [math]\displaystyle{ \epsilon_{\mu} }[/math] | ||
| 1 | исходящий фотон | [math]\displaystyle{ \epsilon^*_{\mu} }[/math] | ||
| Пропагаторы (внутренние линии) |
0 | бозон | [math]\displaystyle{ \frac{i}{q^2 - m^2} }[/math] | |
| ½ | фермион | [math]\displaystyle{ \frac{i(q\!\!\!/ + m)}{q^2 - m^2} }[/math] | ||
| 1 | безмассовая частица (фотон) |
[math]\displaystyle{ \frac{-ig_{\mu\nu}}{q^2} }[/math] | ||
| 1 | массивная частица (бозон) |
[math]\displaystyle{ \frac{-i(g_{\mu\nu} - q_{\mu}q_{\nu}/m^2)}{q^2 - m^2} }[/math] | ||
| Вершина | 
|
[math]\displaystyle{ -ig_e\gamma^{\mu} }[/math] |
- [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] — дираковские спиноры, причём для [math]\displaystyle{ u(p) }[/math] нормирован: [math]\displaystyle{ \bar u(p)u(p) = 2m }[/math],
- [math]\displaystyle{ \epsilon_{\mu} }[/math] — вектор круговой поляризации фотона,
- [math]\displaystyle{ m }[/math] — масса частицы,
- [math]\displaystyle{ i }[/math] — мнимая единица,
- [math]\displaystyle{ q\!\!\!/ = \gamma^\mu q_\mu }[/math] — обозначение для четырёхимпульса [math]\displaystyle{ q_\mu }[/math] и матрицы Дирака [math]\displaystyle{ \gamma^\mu }[/math],
- [math]\displaystyle{ g_{\mu\nu} }[/math] — метрика Минковского,
- [math]\displaystyle{ g_e }[/math] — заряд электрона.
Квантовая хромодинамика
Правила Фейнмана в квантовой хромодинамике[27]:
Слабое взаимодействие
Правила Фейнмана для слабого взаимодействия[72]:
| Категория | Символ | Частица (ы) | Коэффициент умножения | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Вершина | 
|
W-бозон, лептон и его нейтрино | [math]\displaystyle{ \frac{-ig_w}{2\sqrt2}\gamma^\mu(1 - \gamma^5) }[/math] | ||||||||||||||

|
qi — это u-кварк, c-кварк или t-кварк, qj — это d-кварк, s-кварк или b-кварк |
[math]\displaystyle{ \frac{-ig_w}{2\sqrt2}\gamma^\mu(1 - \gamma^5)U_{ij} }[/math] (где U — это CKM-матрица) | |||||||||||||||

|
Z0 бозон, f — кварк или лептон | [math]\displaystyle{ \frac{-ig_z}{2}\gamma^\mu(c_V^f - c_A^f\gamma^5) }[/math]
| |||||||||||||||

|
3 бозона | [math]\displaystyle{ ig_w\cos\theta_w [g_{\nu\lambda}(q_1-q_2)_\mu }[/math]
[math]\displaystyle{ + }[/math] [math]\displaystyle{ g_{\lambda\mu}(q_2-q_3)_\nu }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ g_{\mu\nu}(q_3-q_1)_\lambda] }[/math] | |||||||||||||||

|
2 W-бозона и фотон | [math]\displaystyle{ ig_e [g_{\nu\lambda}(q_1-q_2)_\mu }[/math]
[math]\displaystyle{ + }[/math] [math]\displaystyle{ g_{\lambda\mu}(q_2-q_3)_\nu }[/math] [math]\displaystyle{ + }[/math] [math]\displaystyle{ g_{\mu\nu}(q_3-q_1)_\lambda] }[/math] | |||||||||||||||

|
2 W-бозона и 2 Z-бозона | [math]\displaystyle{ -ig_w^2\cos^2\theta_w (2g_{\mu\nu}g_{\lambda\sigma} - g_{\mu\lambda}g_{\nu\sigma} - g_{\mu\sigma}g_{\nu\lambda}) }[/math] | |||||||||||||||

|
2 W+ бозона и 2 W- бозона | [math]\displaystyle{ ig_w^2 (2g_{\mu\lambda}g_{\nu\sigma} - g_{\mu\nu}g_{\lambda\sigma} - g_{\mu\sigma}g_{\nu\lambda}) }[/math] | |||||||||||||||

|
2 W-бозона и 2 фотона | [math]\displaystyle{ -ig_e^2 (2g_{\mu\nu}g_{\lambda\sigma} - g_{\mu\lambda}g_{\nu\sigma} - g_{\mu\sigma}g_{\nu\lambda}) }[/math] | |||||||||||||||

|
2 W-бозона, Z-бозон и фотон | [math]\displaystyle{ -ig_e g_w \cos\theta_w (2g_{\mu\nu}g_{\lambda\sigma} - g_{\mu\lambda}g_{\nu\sigma} - g_{\mu\sigma}g_{\nu\lambda}) }[/math] |
Приложения
Большинство известных свойств частиц были определены экспериментами связанными с рассеянием частиц[73]. Одной из целей диаграмм Фейнмана является вычисление теоретического эффективного сечения рассеяния и сравнения его с экспериментальными значениями. Как только правила Фейнмана установлены, достаточно применить этот рецепт к данному физическому процессу, чтобы вычислить его амплитуду: выбрать сталкивающиеся и вылетающие частицы, нарисовать все возможные диаграммы с нужной точностью, написать формулы для амплитуд каждой диаграммы, согласно правилам, и просуммировать все эти формулы, чтобы получить амплитуду процесса[74].
Реакция [math]\displaystyle{ e^+ e^- \rightarrow \mu^+ \mu^- }[/math]
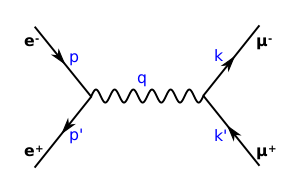
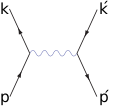
Реакция аннигиляции электрон-позитронной пары, дающая пару мюон-антимюон, является простейшей и наиболее важной в квантовой электродинамике[75].
Амплитуда перехода этой реакции записывается:
- [math]\displaystyle{ \mathcal{M} \sim \langle \mu^+ \mu^- \mid H_I \mid \gamma \rangle^{\mu} \langle \gamma \mid H_I \mid e^+e^- \rangle_{\mu}\,, }[/math]
где [math]\displaystyle{ \mid e^+e^- \rangle }[/math] — множитель, соответствующий внешним линиям диаграммы для позитрона и электрона, [math]\displaystyle{ \langle \mu^+ \mu^- \mid }[/math] — фактор для антимюона и мюона, [math]\displaystyle{ H_I }[/math] — вершины (часть оператора Гамильтона отвечающего за взаимодействия), [math]\displaystyle{ \mid \gamma \rangle \langle \gamma \mid }[/math], оператор внутренней линии фотона[76].
Используя правила Фейнмана:
- [math]\displaystyle{ \mathcal{M} = \overline{v}^{s'}({p'})(-ie\gamma^{\mu})u^s(p) (\frac{-ig_{\mu\nu}}{q^2}) \overline{u}^{r}({k})(-ie\gamma^{\nu})v^{r'}(k')\,, }[/math]
где [math]\displaystyle{ u }[/math], [math]\displaystyle{ v }[/math], [math]\displaystyle{ \overline{u} }[/math] и [math]\displaystyle{ \overline{v} }[/math] — спиноры внешних линий, причем [math]\displaystyle{ s }[/math], [math]\displaystyle{ s' }[/math], [math]\displaystyle{ r }[/math], и [math]\displaystyle{ r' }[/math] их спины, [math]\displaystyle{ -ie\gamma^{\mu} }[/math] и [math]\displaystyle{ -ie\gamma^{\nu} }[/math] — вершины ([math]\displaystyle{ H_I }[/math]) и [math]\displaystyle{ \frac{-ig_{\mu\nu}}{q^2} }[/math] соответствует линии фотона (оператор [math]\displaystyle{ \mid \gamma \rangle \langle \gamma \mid }[/math])[77][78].
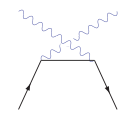
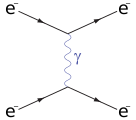
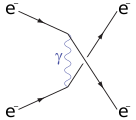
Рассеяние Баба
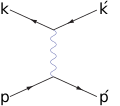
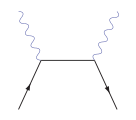
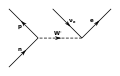
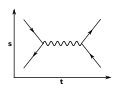
Рассеяние Баба — это процесс рассеяния между элементарной частицей и её античастицей, то есть электроном и позитроном в квантовой электродинамике[79]. Он описывается двумя диаграммами: классического рассеяния и аннигиляции с рождением пар[80].
-
Аннигиляция (s канал)
-
Рассеяние (t канал)
Каналы [math]\displaystyle{ s }[/math] и [math]\displaystyle{ t }[/math] определяются переменными Мандельштама[81]. Благодаря правилам Фейнмана запишем для каждой диаграммы (и, следовательно, для каждого канала) матричный элемент:
- [math]\displaystyle{ \mathcal M_s = \bar v(k) \mathrm i e \gamma^\mu u(p) \frac{\mathrm i g_{\mu\nu}}{(k + p)^2} \bar u(p') \mathrm i e \gamma^\nu v(k')\,, }[/math]
- [math]\displaystyle{ \mathcal M_t = \bar v(k) \mathrm i e \gamma^\rho v(k') \frac{\mathrm i g_{\rho\sigma}}{(k' - k)^2} \bar u(p') \mathrm i e \gamma^\sigma u(p)\,, }[/math]
где [math]\displaystyle{ k }[/math] и [math]\displaystyle{ k' }[/math] — четырёхимпульсы позитрона, [math]\displaystyle{ p }[/math] и [math]\displaystyle{ p' }[/math] — электрона, [math]\displaystyle{ v }[/math] и [math]\displaystyle{ \bar v }[/math] — позитронные спиноры, [math]\displaystyle{ u }[/math] и [math]\displaystyle{ \bar u }[/math] — электронные, [math]\displaystyle{ \gamma^\mu }[/math], [math]\displaystyle{ \gamma^\nu }[/math], [math]\displaystyle{ \gamma^\rho }[/math] и [math]\displaystyle{ \gamma^\sigma }[/math] — матрицы Дирака[82].
Эффект Комптона
Эффект Комптона — это неупругое рассеяние фотона веществом. Следующие диаграммы дают представление о двух возможных порядках поглощения и испускания фотонов[83].
- Эффект Комптона
-
Последний фотон, испущенный после
-
Последний фотон, испущенный до
Если мы напишем этот процесс [math]\displaystyle{ e^-(p)\gamma(k) \to e^-(p')\gamma(k') }[/math] с участием [math]\displaystyle{ \epsilon }[/math] исходный фотон и [math]\displaystyle{ \epsilon' }[/math] рассеянный фотон, то правила Фейнмана дают для амплитуд двух диаграмм[84][85]:
- [math]\displaystyle{ \mathcal M_1 = \bar u(p') (-ie\gamma^\mu) \frac{i(q\!\!\!/ + m)}{q^2 - m^2} (-ie\gamma^\mu) u(p) \epsilon'_\mu \epsilon_\nu\,, }[/math]
- [math]\displaystyle{ \mathcal M_2 = \bar u(p') (-ie\gamma^\mu) \frac{i(q\!\!\!/ + m)}{q^2 - m^2} (-ie\gamma^\mu) u(p) \epsilon'_\nu \epsilon_\mu\,. }[/math]
Рассеяние Мёллера
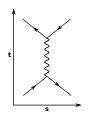
Мёллеровское рассеяние[англ.] описывает рассеяние двух электронов: [math]\displaystyle{ e^- e^- \rightarrow e^- e^- }[/math], и включает каналы [math]\displaystyle{ t }[/math] и [math]\displaystyle{ u }[/math] Мандельштама[81].
-
Канал t
-
Канал u
Лэмбовский сдвиг
Лэмбовский сдвиг представляет собой разницу между двумя определёнными уровнями тонкой структуры атома водорода [math]\displaystyle{ 2S_{1/2} }[/math] и [math]\displaystyle{ 2P_{1/2} }[/math]. Первые три вклада в этот сдвиг представлены следующими диаграммами, дающими по порядку перенормировку массы электрона, его аномального магнитного момента и поляризации вакуума, что в сумме дают 1058 MHz по сравнению с предсказанием для сдвига из уравнения Дирака, которое даёт вырождение[86].
- Первые три вклада в лэмбовский сдвиг
-
1017 MHz
-
68 MHz
-
-27 MHz
Квантовые флуктуации вакуума


Фотоны, излучаемые, а затем повторно поглощаемые одним и тем же электроном, являются виртуальными фотонами из-за взаимодействия с квантовыми флуктуациями в вакууме. Следующие диаграммы также представляют собственно-энергетические части электрона с несколькими петлями[88].
- Петли собственной энергетической части
-
-
-
Реакция [math]\displaystyle{ e^+ e^- \rightarrow }[/math] адроны

В квантовой хромодинамике электрон-позитронная аннигиляция, которая рождает пару кварков, включает в качестве первой поправки три различные диаграммы, все с обменом глюоном[89].
- Вклады порядка α
-
-
-
Критика и другие теории
Диаграммы Фейнмана используются для расчёта амплитуд рассеяния уже более 60 лет, но, несмотря на их эффективность, они не позволяют справиться со сложными реакциями даже на самых современных компьютерах: количество членов, необходимых для учёта более высокого порядка теории возмущений, увеличивается экспоненциально. Новая методика под названием «метод унитарности» преодолевает эту проблему[90]. В квантовой хромодинамике анализ рассеяния двух глюонов, дающий три глюона, оказался слишком сложен на языке диаграмм. Этот новый метод даёт простую формулу, которая умещается на странице и позволяет понять реакцию, используя принцип унитарности, принцип, неявный в диаграммах Фейнмана, поскольку он маскируется сложностью вычислений. Хотя этот принцип использовался в 1960-х годах, он был выдвинут этой новой техникой. Это позволяет избежать необходимости прибегать к виртуальным частицам, источнику сложности диаграмм: когда метод Фейнмана складывает все возможные диаграммы реакции, включая те, которые кажутся невозможными, даже если они в конечном итоге компенсируют друг друга, метод унитарности рассматривает только полезные реакции[91].
Использование вне элементарных взаимодействий
Формализм диаграмм Фейнмана, в их графическом представлении или в виде лежащих в их основе математических идеях, используется во многих областях физики[92].
В ядерной физике процессы близки к элементарным взаимодействиям. Уравнения и измерения аналогичны, поскольку амплитуды также рассчитываются для проверки сечений[93].
Точно так же в физике конденсированного состояния, наиболее важной подобластью которой является физика твердого тела, теоретическое описание использует объекты, называемые квазичастицами, которые могут быть описаны функциями Грина и, следовательно, пропагаторами, как для элементарных частиц. Таким образом, эти взаимодействия рассчитываются с помощью диаграмм Фейнмана[94].
- Диаграммы для других разделов физики
-
Ядерная физика -
Собственная энергетическая часть в физике конденсированного состояния
В искусстве

Ричард Фейнман купил пикап в 1975 году и зарегистрировал номер QANTUM. На машине он нарисовал придуманные им схемы. Пикап, проданный женой, после смерти учёного, продолжал использоваться. Шеймус Блэкли купил машину в 2012 году и переделал стёртые диаграммы, чтобы пересечь Соединённые Штаты с передвижной выставкой, организованной Эдвардом Тафти и лабораторией Ферми[95][96].
Этот пикап появился в 2015 году в третьем эпизоде девятого сезона телесериала «Теория большого взрыва» под названием «Коррозия мальчишника»[97][98]. В этой серии, в которой участвуют два физика, много ссылок на Фейнмана и несколько раз показаны его диаграммы; электронно-мюонная реакция появляется, в частности, в тринадцатом эпизоде первого сезона, «Теория Большого взрыва (сезон 1)», чтобы решить исход состязания между двумя командами-финалистами физического конкурса[99].
Инженер-физик Эндрю Чараламбус (англ. Andrew Charalambous) создал множество произведений искусства, изображающих диаграммы Фейнмана, как из-за энтузиазма, так и для их популяризации[100][101].
Содержащиеся в диаграммах идеи, такие как античастицы, представленные указывающими в противоположном направлении времени стрелками, вдохновили нескольких писателей-фантастов: концепция обратной причинности, обоснованная теорией Фейнмана, появляется в романе Стивена Бакстера «Время» для передачи сообщений в прошлое или в фильме «Детонатор» Шейна Кэррута для путешествий во времени[102][103].
Примечания и ссылки
Комментарии
- ↑ Like the silicon chip of more recent years, the Feynman diagram was bringing computation to the masses.
- ↑ Эта презентация проходила в горах Поконо и поэтому называется конференция в Поконо[англ.].
- ↑ Две книги были опубликованы в 1953 г., одна в Японии (Умэдзава), а другая в России (Ахиезер и Берестецкий), но не были переведены на английский язык до 1956 и 1957 гг. соответственно.
- ↑ Dans Einführung in die Quantentheorie der Wellenfelder, paru en 1943.
- ↑ Исторически направление времени вверх исходило из диаграммы Минковского.
- ↑ Амплитуды вероятности являются комплексными функциями.
- ↑ Фейнман использовал интерпретацию Эрнста Штюкельберга для представления позитронов (и других античастиц) как сущностей, уходящих в прошлое.
- ↑ Эта константа связи, [math]\displaystyle{ \alpha = \tfrac{1}{137{,}035\,999\,074(44)} }[/math], что даёт [math]\displaystyle{ e \approx-0,0854245 }[/math], — постоянная тонкой структуры.
Примечания
- ↑ 1,0 1,1 1,2 1,3 Kaiser, 2005, p. 158.
- ↑ O’Dowd, 2017, 3 secondes.
- ↑ 3,0 3,1 Rosenbaum, 2009, p. 151—152.
- ↑ Wüthrich, 2011, p. 1.
- ↑ Kaiser, 2005, p. 9.
- ↑ 6,0 6,1 Rosenbaum, 2009, p. 152.
- ↑ Wüthrich, 2011, p. 5.
- ↑ Kaiser, 2005, p. 17.
- ↑ Kaiser, 2005, p. 27.
- ↑ Kaiser, 2005, p. 161.
- ↑ 11,0 11,1 Rosenbaum, 2009, p. 157.
- ↑ 12,0 12,1 Kaiser, 2005, p. 363.
- ↑ Martin, Rothen, 1990, p. 323.
- ↑ Peskin, Schroeder, 1995, p. 3.
- ↑ 15,0 15,1 15,2 Marleau, 2017, p. 79.
- ↑ Peskin, Schroeder, 1995, p. 716.
- ↑ Baglio, Djouadi, 2011, p. 5—7.
- ↑ Marleau, 2017, p. 315.
- ↑ Ченг и Ли, 1987, с. 452.
- ↑ Ченг и Ли, 1987, с. 243.
- ↑ Griffiths, 2008, p. 321.
- ↑ Griffiths, 2008, p. 319.
- ↑ 23,0 23,1 Feynman, 1992, p. 119.
- ↑ Feynman, 1992, p. 120.
- ↑ Griffiths, 2004, p. 57.
- ↑ Feynman, 1992, p. 126.
- ↑ 27,0 27,1 Griffiths, 2004, p. 283.
- ↑ Marleau, 2017, p. 81.
- ↑ O’Dowd, 2017, 5 min 25 s.
- ↑ Taillet, Villain, Febvre, 2013, entrée «couche de masse», p. 152.
- ↑ 31,0 31,1 31,2 31,3 31,4 Ширков, Д. В. Фёйнмана диаграммы // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 277279. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ O’Dowd, 2017, 5 min 58 s.
- ↑ 33,0 33,1 Griffiths, 2004, p. 59.
- ↑ Tatsumi Aoyama (2012). «Tenth-Order QED Contribution to the Electron g – 2 and an Improved Value of the Fine Structure Constant» (en). Physical Review Letters 109 (11—14): 4. arXiv:1205.5368. doi:10.1103/PhysRevLett.109.111807.
- ↑ Feynman, 1949, p. 753.
- ↑ O’Dowd, 2017, 2 min 2 s.
- ↑ O’Dowd, 2017, 2 min 59 s.
- ↑ O’Dowd, 2017, 4 min 30 s.
- ↑ Griffiths, 2004, p. 61.
- ↑ Peskin, Schroeder, 1995, p. 548.
- ↑ Kaiser, 2005, p. 374.
- ↑ Peskin, Schroeder, 1995, p. 551.
- ↑ Griffiths, 2004, p. 301.
- ↑ Ченг и Ли, 1987, с. 588—593.
- ↑ Martin, Rothen, 1990, p. 369.
- ↑ Martin, Rothen, 1990, p. 373.
- ↑ Бьёркен и Дрелл, т. 2, 1978, с. 190.
- ↑ Wüthrich, 2011, p. 2.
- ↑ Peskin, Schroeder, 1995, p. 4.
- ↑ 50,0 50,1 Peskin, Schroeder, 1995, p. 5.
- ↑ Rosenbaum, 2009, p. 158.
- ↑ 52,0 52,1 Rosenbaum, 2009, p. 159.
- ↑ Rosenbaum, 2009, p. 162.
- ↑ Wüthrich, 2011, p. 16.
- ↑ Kaiser, 2005, p. 160.
- ↑ O’Dowd, 2017, 1 min 28 s.
- ↑ Kaiser, 2005, p. 157.
- ↑ O’Dowd, 2017, 25 secondes.
- ↑ O’Dowd, 2017, 57 secondes.
- ↑ O’Dowd, 2017, 1 min 12 s.
- ↑ 61,0 61,1 Marleau, 2017, p. 19.
- ↑ 62,0 62,1 Marleau, 2017, p. 20.
- ↑ Marleau, 2017, p. 13.
- ↑ Rosenbaum, 2009, p. 153.
- ↑ 65,0 65,1 Rosenbaum, 2009, p. 154.
- ↑ Rosenbaum, 2009, p. 155.
- ↑ Kaiser, 2005, p. 51.
- ↑ Rosenbaum, 2009, p. 160.
- ↑ Wüthrich, 2011, p. 3.
- ↑ Rosenbaum, 2009, p. 156.
- ↑ Griffiths, 2004, p. 380.
- ↑ Griffiths, 2004, p. 381.
- ↑ Marleau, 2017, p. 59.
- ↑ Marleau, 2017, p. 80—81.
- ↑ Peskin, Schroeder, 1995, p. 131.
- ↑ Peskin, Schroeder, 1995, p. 6.
- ↑ Peskin, Schroeder, 1995, p. 10.
- ↑ Griffiths, 2008, p. 246.
- ↑ Биленький, 1990, с. 143.
- ↑ Пескин и Шрёдер, 2001, с. 165.
- ↑ 81,0 81,1 Peskin, Schroeder, 1995, p. 157.
- ↑ Griffiths, 2008, p. 247—248.
- ↑ Marleau, 2017, p. 45.
- ↑ Marleau, 2017, p. 131.
- ↑ Griffiths, 2008, p. 249.
- ↑ Jean-Christophe Pain (28 octobre 2013). «Willis Eugene Lamb (1913–2008) La passion de la précision». Reflets de la physique (36): 27—29. doi:10.1051/refdp/201336027..
- ↑ Peskin, Schroeder, 1995, p. 336.
- ↑ Marleau, 2017, p. 23.
- ↑ Peskin, Schroeder, 1995, p. 549.
- ↑ Bern, Dixon, Kosower, 2012, p. 36.
- ↑ Bern, Dixon, Kosower, 2012, p. 39.
- ↑ Биленький, 1971, с. 3.
- ↑ Blokhintsev, 2003.
- ↑ Mattuck, 1992, p. 12.
- ↑ Ralph Leighton. The Feynman Van (англ.). feynman.com. Дата обращения: 29 octobre 2017. Архивировано 30 ноября 2017 года..
- ↑ Kathryn Jepsen. Saving the Feynman van (англ.). symmetrymagazine.org (2014). Дата обращения: 29 octobre 2017. Архивировано 30 сентября 2017 года..
- ↑ The Bachelor Party Corrosion (англ.). bigbangtheory.wikia.com. Дата обращения: 29 octobre 2017. Архивировано 29 октября 2017 года..
- ↑ CHUCK LORRE PRODUCTIONS, #503 (англ.). chucklorre.com. Дата обращения: 29 octobre 2017. Архивировано 29 октября 2017 года..
- ↑ Richard Feynman (англ.). bigbangtheory.wikia.com. Дата обращения: 29 octobre 2017. Архивировано 29 октября 2017 года..
- ↑ Katherine Wright. Arts & Culture: Feynman for All (англ.). APS (23 juin 2016). Дата обращения: 29 octobre 2017. Архивировано 29 октября 2017 года.
- ↑ Andrew Charalambous. Feynman inspired art (англ.) (pdf). cds.cern.ch (2016). Дата обращения: 29 octobre 2017. Архивировано 1 января 2022 года..
- ↑ Time Radio (англ.). sf-encyclopedia.com (4 mai 2015). Дата обращения: 29 octobre 2017. Архивировано 30 октября 2017 года..
- ↑ Grant Watson. “The answer was unknowable” (англ.). fictionmachine.com (18 juin 2014). Дата обращения: 29 octobre 2017. Архивировано 29 октября 2017 года..
Библиография
Книги и статьи
- Биленький, Самоил Михелевич. Введение в диаграммную технику Фейнмана. — М.: Атомиздат, 1971. — 216 с.
- Биленький С. М. Введение в диаграммы Фейнмана и физику электрослабого взаимодействия. — М.: Энергоатомиздат, 1990. — 327 с. — ISBN 5-283-03930-7.
- Бьёркен Дж. Д., Дрелл С. Д. Релятивистская квантовая теория. Релятивистские квантовые поля. — М.: Наука, 1978. — Т. 2. — 408 с.
- * Пескин М., Шрёдер Д. Введение в квантовую теорию поля / Ред. пер. А. А. Белавин. — Ижевск: РХД, 2001. — 784 с.
- Ченг Т.-П., Ли Л.-Ф. Калибровочные теории в физике элементарных частиц. — М.: Мир, 1987. — 624 с.
- Julien Baglio (2011). «Higgs production at the lHC» (en). Journal of High Energy Physics. arXiv:1012.0530. doi:10.1007/JHEP03(2011)055. Проверено 14 november 2017..
- Zvi Bern, Lance J. Dixon, David A. Kosower (2012). «Loops, Trees and the Search for New Physics» (en) (pdf). Scientific American 306 (5). doi:10.1038/scientificamerican0512-34..
- L. D. Blokhintsev (2003). «Feynman diagrams in nuclear physics at low and intermediate energies» (en) (pdf). Selected topics in theoretical physics and astrophysics: 99—104..
- Feynman, Richard. Lumière et matière : une étrange histoire. — Paris : InterEditions Seuil, 1992. — ISBN 9782020147583.
- Richard Feynman (1949). «The Theory of Positrons» (en). Physical Review 76 (6): 749—759. 1949Positrons. Проверено 8 october 2017..
- Griffiths, David. Introduction to elementary particles. — New York : Wiley, 2004. — ISBN 9780471603863.
- Griffiths, David. Introduction to elementary particles. — 2nd ed.. — Wiley-VCH, 2008. — 468 с. — ISBN 978-3-527-40601-2.
- 't Hooft, Gerardus. Diagrammar..
- Kaiser, David. Drawing theories apart : the dispersion of Feynman diagrams in postwar physics. — Chicago : University of Chicago Press, 2005. — ISBN 0226422666.
- David Kaiser (2005). «Physics and Feynman’s Diagrams» (en). American Scientist 93: 156—165. 2005Physics. Проверено 8 october 2017.
- Marleau, Luc. Introduction à la physique des particules. — 2017. — P. 413.
- Martin, Philippe. Problèmes à N-corps et champs quantiques : Cours élémentaire. — Lausanne : Presses polytechniques et universitaires romandes, 1990. — ISBN 2880741939.
- Mattuck, Richard. A guide to Feynman diagrams in the many-body problem. — New York : Dover Publications, 1992. — ISBN 9780486670478.
- Peskin, Michael. An Introduction To Quantum Field Theory. — New York : Westview Press, 1995. — ISBN 0201503972.
- Alexis Rosenbaum (2009). «Sur le statut des diagrammes de Feynman en théorie quantique des champs». Philosophia Scientiæ 13 (2): 151—166. doi:10.4000/philosophiascientiae.301. Проверено 19 september 2017.
- Taillet, Richard. Dictionnaire de physique : + de 6000 termes, nombreuses références historiques, 3700 référence bibliographiques. — Bruxelles : De Boeck, 2013. — ISBN 9782804175542.
- Veltman, Martinus. Diagrammatica : the path to Feynman rules. — Cambridge : Cambridge University Press, 1994. — ISBN 0521456924.
- Wüthrich, Adrian. The genesis of Feynman diagrams. — Dordrecht New York : Springer Science+Business Media B.V, 2011. — ISBN 9789048192274.
- Zee, A. Quantum field theory in a nutshell. — Princeton, N.J : Princeton University Press, 2010. — ISBN 9780691140346.
Конференции и видео
- Gilles Cohen-Tannoudji. Les diagrammes de Feynman, la partition du modèle standard (MP3, MP4, MOV, WMV). École normale supérieure (Paris): Collectif Histoire Philosophie Sciences.
- Matt O’Dowd. Solving the Impossible in Quantum Field Theory (YouTube). PBS Space Time.
- Matt O’Dowd. The Secrets of Feynman Diagrams (YouTube). PBS Space Time.
Связанная статья
Внешняя ссылка
- Lincoln, Don. Feynman diagrams (англ.). YouTube (2016).
- Aivazis, Alec. Draw Feynman Diagram Online (англ.). Дата обращения: 23 января 2022. (англ.) Онлайн-инструмент для рисования диаграмм Фейнмана
- The JaxoDraw team. JaxoDraw (англ.). Дата обращения: 23 января 2022. (англ.) Программа для рисования диаграмм Фейнмана.
- Goossens, Michel. Drawing Feynman Diagrams with LaTeX and METAFONT (or METAPOST) (англ.). Дата обращения: 23 января 2022. (англ.) Построение диаграмм Фейнмана в LaTeX
- Dimm, Bill. Drawing Feynman Diagrams with LaTeX and METAFONT (or METAPOST) (англ.). Дата обращения: 23 января 2022. (англ.) Построение диаграмм Фейнмана на C++









![Электрон излучает фотон : [math]\displaystyle{ e^- \to e^- + \gamma }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_electron_emits_photon.svg&width=119)
![Электрон поглощает фотон : [math]\displaystyle{ e^- + \gamma \to e^- }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_electron_absorbs_photon.svg&width=119)
![Позитрон излучает фотон : [math]\displaystyle{ e^+ \to e^+ + \gamma }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_positron_emits_photon.svg&width=119)
![Позитрон поглощает фотон : [math]\displaystyle{ e^+ + \gamma \to e^+ }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_positron_absorbs_photon.svg&width=119)
![Позитрон и электрон аннигилируют в фотоне : [math]\displaystyle{ e^+ + e^- \to \gamma }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_electron_and_positron_annihilate.svg&width=119)
![Фотон создает электрон и позитрон : [math]\displaystyle{ \gamma \to e^- + e^+ }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Basic_Feynman_diagram_-_pair_production.svg&width=119)