Спин

Спин (от англ. spin, букв. — «вращение, вращать(-ся)») — собственный момент импульса элементарных частиц, имеющий как квантовую, так и классическую природу и тесно связанный с представлениями группы вращений и группы Лоренца (классические аспекты спина см. в книгах H.C. Corben, Classical and Quantum Theories of Spinning Particles (Holden-Day, San Francisco, 1968), Alexei Deriglazov, Classical Mechanics (Second Edition,  Springer 2017), Пенроуз и Риндлер, Спиноры и пространство-время). Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

Спин измеряется в единицах ħ (приведённой постоянной Планка, или постоянной Дирака) и равен ħJ, где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число (оно есть число, характеризующее представления группы вращений и группы Лоренца, то есть сколько в нём собственно квантовости и сколько неквантовости, сейчас неизвестно), которое обычно называют просто спином (одно из квантовых чисел). Спин свободной частицы измерить нельзя, так как для измерения требуется внешнее магнитное поле, а оно делает частицу несвободной.

В связи с этим говорят о целом или полуцелом спине частицы. Полуцелый спин фундаментальнее, так как "из него" можно построить целый спин, но обратное невозможно (см. книгу Пенроуза и Риндлера).

Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантово-механического явления, не имеющего аналогии в классической механике: обменного взаимодействия.

Вектор спина является единственной величиной, характеризующей ориентацию частицы в квантовой механике. Из этого положения следует, что: при нулевом спине у частицы не может существовать никаких векторных и тензорных характеристик; векторные свойства частиц могут описываться только аксиальными векторами; частицы могут иметь магнитные дипольные моменты и не могут иметь электрических дипольных моментов; частицы могут иметь электрический квадрупольный момент и не могут иметь магнитный квадрупольный момент; отличный от нуля квадрупольный момент возможен лишь у частиц при спине, не меньшем единицы.

Спиновый момент электрона или другой элементарной частицы, однозначно отделённый от орбитального момента, никогда не может быть определён посредством опытов, к которым применимо классическое понятие траектории частицы.

Число компонент волновой функции, описывающей элементарную частицу в квантовой механике, растёт с ростом спина элементарной частицы. Элементарные частицы со спином [math]\displaystyle{ 0 }[/math] описываются однокомпонентной волновой функцией (скаляр), со спином [math]\displaystyle{ \frac{1}{2} }[/math] описываются двухкомпонентной волновой функцией (спинор), со спином [math]\displaystyle{ 1 }[/math] описываются трёхкомпонентной волновой функцией (вектор), со спином [math]\displaystyle{ 2 }[/math] описываются пятикомпонентной волновой функцией (тензор).

Что такое спин — на примерах

Пример объекта, который требует поворота на 720° для возврата в начальное положение

Основной источник: Видеозапись лекции - что такое спин (неопр.).

Хотя термин «спин» относится только к квантовым свойствам частиц, свойства некоторых циклически действующих макроскопических систем тоже могут быть описаны неким числом, которое показывает, на сколько частей нужно разделить цикл вращения некоего элемента системы, чтобы она вернулась в состояние, неотличимое от начального.

Легко представить себе спин, равный 0: это точка — она со всех сторон выглядит одинаково, как её ни крути.

Примером спина, равного 1, может служить большинство обычных предметов без какой-либо симметрии: если такой предмет повернуть на 360°, то этот предмет вернётся в своё первоначальное состояние. Для примера — можно положить ручку на стол, и после поворота на 360° ручка опять будет лежать так же, как и до поворота.

В качестве примера спина, равного 2, можно взять любой предмет с одной осью центральной симметрии: если его повернуть на 180°, он будет неотличим от исходного положения, и получается, что за один полный оборот он становится неотличим от исходного положения 2 раза. Примером из жизни может служить обычный карандаш, только заточённый с двух сторон или не заточённый вообще — главное чтобы был без надписей и однотонный — и тогда после поворота на 180° он вернётся в положение, неотличимое от исходного. Хокинг в качестве примера приводил обычную игральную карту типа короля или дамы

Четырёхтактный двигатель возвращается в исходное состояние при повороте коленчатого вала на 720°, что является неким аналогом полуцелого спина

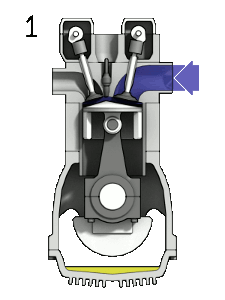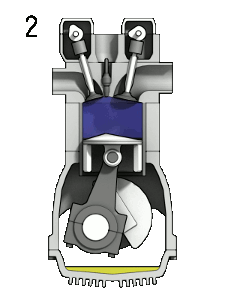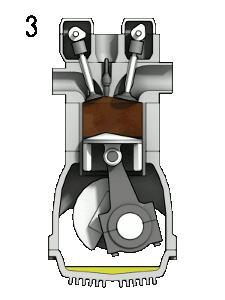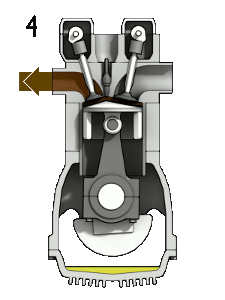
А вот с полуцелым спином, равным ¹/₂ немножко сложнее: в исходное положение система возвращается после 2 полных оборотов, то есть после поворота на 720°. Примеры:

• Если взять ленту Мёбиуса и представить, что по ней ползёт муравей, тогда, сделав один оборот (пройдя 360°), муравей окажется в той же точке, но с другой стороны листа, а чтобы вернуться в точку, откуда он начал, придётся пройти все 720°.
• Четырёхтактный двигатель внутреннего сгорания. При повороте коленчатого вала на 360° поршень вернётся в исходное положение (например, верхнюю мёртвую точку), но распределительный вал вращается в 2 раза медленнее и совершит полный оборот при повороте коленчатого вала на 720°. То есть при повороте коленчатого вала на 2 оборота двигатель внутреннего сгорания вернётся в то же состояние. В этом случае третьим измерением будет положение распределительного вала.

На подобных примерах можно проиллюстрировать сложение спинов:

• Два заточенных только с одной стороны одинаковых карандаша («спин» каждого — 1), скреплённые боковыми сторонами друг с другом так, что острый конец одного будет рядом с тупым концом другого (↑↓). Такая система вернётся в неотличимое от начального состояния при повороте всего на 180°, то есть «спин» системы стал равным двум.
• Многоцилиндровый четырёхтактный двигатель внутреннего сгорания («спин» каждого из цилиндров которого равен 1/2). Если все цилиндры работают одинаково, то состояния, при которых поршень находится в начале такта рабочего хода в любом из цилиндров, будут неотличимы. Следовательно, двухцилиндровый двигатель будет возвращаться в состояние, неотличимое от исходного, через каждые 360° (суммарный «спин» — 1), четырёхцилиндровый — через 180° («спин» — 2), восьмицилиндровый — через 90° («спин» — 4).

Свойства спина

Любая частица может обладать двумя видами углового момента: орбитальным угловым моментом и спином.

В отличие от орбитального углового момента, который порождается движением частицы в пространстве, спин не связан с движением в пространстве. Спин — это внутренняя, исключительно квантовая характеристика, которую нельзя объяснить в рамках релятивистской механики. Если представлять частицу (например, электрон) как вращающийся шарик, а спин как момент, связанный с этим вращением, то оказывается, что поперечная скорость движения оболочки частицы должна быть выше скорости света, что недопустимо с позиции релятивизма.

В частности, было бы совершенно бессмысленным представлять себе собственный момент элементарной частицы, как результат ее вращения „вокруг собственной оси“

Будучи одним из проявлений углового момента, спин в квантовой механике описывается векторным оператором спина [math]\displaystyle{ \hat{\vec{s}}, }[/math] алгебра компонент которого полностью совпадает с алгеброй операторов орбитального углового момента [math]\displaystyle{ \hat{\vec{\ell}}. }[/math] Однако, в отличие от орбитального углового момента, оператор спина не выражается через классические переменные, иными словами, это только квантовая величина. Следствием этого является тот факт, что спин (и его проекции на какую-либо ось) может принимать не только целые, но и полуцелые значения (в единицах постоянной Дирака ħ).

Спин испытывает квантовые флуктуации. В результате квантовых флуктуаций строго определённое значение может иметь только одна компонента спина — например, [math]\displaystyle{ J_{z} }[/math]. При этом компоненты [math]\displaystyle{ J_{x}, J_{y} }[/math] флуктуируют вокруг среднего значения. Максимально возможное значение компоненты [math]\displaystyle{ J_{z} }[/math] равно [math]\displaystyle{ J }[/math]. В то же время квадрат [math]\displaystyle{ J^2 }[/math] всего вектора спина равен [math]\displaystyle{ J(J+1) }[/math]. Таким образом, [math]\displaystyle{ J_{x}^{2}+J_{y}^{2}=J^{2}-J_{z}^{2} \geqslant J }[/math]. При [math]\displaystyle{ J=\frac{1}{2} }[/math] среднеквадратические значения всех компонентов из-за флуктуаций равны [math]\displaystyle{ \widehat{J_{x}^{2}} = \widehat{J_{y}^{2}} =\widehat{J_{z}^{2}} = \frac{1}{4} }[/math].

Вектор спина меняет своё направление при преобразовании Лоренца. Ось этого поворота перпендикулярна импульсу частицы и относительной скорости систем отсчёта.

Примеры

Ниже указаны спины некоторых микрочастиц.

спин	общее название частиц	примеры
0	скалярные частицы	π-мезоны, K-мезоны, хиггсовский бозон, атомы и ядра 4He, чётно-чётные ядра, парапозитроний
1/2	спинорные частицы	электрон, кварки, мюон, тау-лептон, нейтрино, протон, нейтрон, атомы и ядра 3He
1	векторные частицы	фотон, глюон, W- и Z-бозоны, векторные мезоны, ортопозитроний
3/2	спин-векторные частицы	Ω-гиперон, Δ-резонансы
2	тензорные частицы	гравитон, тензорные мезоны

На июль 2004 года максимальным спином среди известных барионов обладал барионный резонанс Δ(2950) со спином [math]\displaystyle{ 15/2 }[/math]. Среди долгоживущих изотопов химических элементов максимальным спином обладает изотоп висмута ²⁰⁹Bi, его спин составляет [math]\displaystyle{ 9/2 }[/math]. Некоторые короткоживущие изотопы и особенно изомеры могут иметь очень высокий спин, например у изотопа таллия^205m2Tl спин [math]\displaystyle{ 35/2 }[/math], а изотоп полония ^211m3Po имеет спин [math]\displaystyle{ 43/2 }[/math].

История

В 1922 году опыт Штерна — Герлаха подтвердил наличие у атомов спина и факт пространственного квантования направления их магнитных моментов.

Сам термин «спин» в науку ввели С. Гаудсмит и Д. Уленбек в 1925 г..

В 1924 году, ещё до точной формулировки квантовой механики, Вольфганг Паули ввёл новую, двухкомпонентную внутреннюю степень свободы для описания валентного электрона в щелочных металлах. В 1927 году он же модифицировал недавно открытое уравнение Шрёдингера для учёта спиновой переменной. Модифицированное таким образом уравнение носит сейчас название уравнение Паули. При таком описании у электрона появляется новая спиновая часть волновой функции, которая описывается спинором — «вектором» в абстрактном (то есть не связанном прямо с обычным) двумерном спиновом пространстве.

В 1928 году Поль Дирак построил релятивистскую теорию спина и ввёл уже четырёхкомпонентную величину — биспинор.

Математически теория спина оказалась очень продуктивной, и в дальнейшем по аналогии с ней была построена теория изоспина.

Спин и магнитный момент

Орбитальный магнитный момент электрона внутри атома кратен магнетону Бора. Но помимо орбитального момента количества движения [math]\displaystyle{ M_l }[/math], обусловленного движением вокруг атомного ядра, электрон обладает собственным механическим моментом — спином [math]\displaystyle{ s = 1/2 }[/math] (в единицах ħ), а также спиновым магнитным моментом (который по факту не кратен магнетону Бора). Спиновый магнитный момент [math]\displaystyle{ \mu_s = g_e \mu_B s }[/math], где [math]\displaystyle{ g_e }[/math] — g-фактор электрона, равный для электрона по данным экспериментов ~2,00231930436153.

Спин и статистика

Вследствие того, что все элементарные частицы одного и того же сорта тождественны, волновая функция системы из нескольких одинаковых частиц должна быть либо симметричной (то есть не изменяется), либо антисимметричной (домножается на −1) относительно перестановки местами двух любых частиц. В первом случае говорят, что частицы подчиняются статистике Бозе — Эйнштейна и называются бозонами. Во втором случае частицы описываются статистикой Ферми — Дирака и называются фермионами.

Оказывается, именно значение спина частицы говорит о том, каковы будут эти симметрийные свойства. Сформулированная Вольфгангом Паули в 1940 году теорема о связи спина со статистикой утверждает, что частицы с целым спином (s = 0, 1, 2, …) являются бозонами, а частицы с полуцелым спином (s = 1/2, 3/2, …) — фермионами.

Обобщение спина

Введение спина является удачным применением новой физической идеи: постулирование того, что существует пространство состояний, никак не связанных с перемещением частицы в обычном пространстве. Обобщение этой идеи в ядерной физике привело к понятию изотопического спина, который действует в особом изоспиновом пространстве. В дальнейшем при описании сильных взаимодействий были введены внутреннее цветовое пространство и квантовое число «цвет» — более сложный аналог спина.

Спин классических систем

Понятие спина было введено в квантовой теории. Тем не менее, в релятивистской механике можно определить спин классической (не квантовой) системы как собственный момент импульса. Классический спин является 4-вектором и определяется следующим образом:

[math]\displaystyle{ S_\nu = \frac{1}{2}\,\varepsilon_{\nu\alpha\beta\gamma}\,L^{\alpha\beta}\,U^\gamma, }[/math]

где

[math]\displaystyle{ L^{\alpha\beta}=\sum (x^\alpha p^\beta-x^\beta p^\alpha) }[/math] — тензор полного момента импульса системы (суммирование проводится по всем частицам системы);

[math]\displaystyle{ U^{\alpha}=P^\alpha/M }[/math] — суммарная 4-скорость системы, определяемая при помощи суммарного 4-импульса [math]\displaystyle{ P^\alpha=\sum p^\alpha }[/math] и массы M системы;

[math]\displaystyle{ \varepsilon_{\nu\alpha\beta\gamma} }[/math] — тензор Леви-Чивиты.

В силу антисимметрии тензора Леви-Чивиты, 4-вектор спина всегда ортогонален к 4-скорости [math]\displaystyle{ U^{\alpha}. }[/math] В системе отсчёта, в которой суммарный импульс системы равен нулю, пространственные компоненты спина совпадают с вектором момента импульса, а временная компонента равна нулю.

Именно поэтому спин называют собственным моментом импульса.

В квантовой теории поля это определение спина сохраняется. В качестве момента импульса и суммарного импульса выступают интегралы движения соответствующего поля. В результате процедуры вторичного квантования 4-вектор спина становится оператором с дискретными собственными значениями.

См. также

• Прецессия Томаса
• Спин-орбитальное взаимодействие
• Преобразование Гольштейна — Примакова
• Спинор
• Теорема Паули (Теорема о связи спина со статистикой)
• Синглет
• Спин-запрещенные реакции

Литература

• Физическая энциклопедия / Под ред. А. М. Прохорова. — М.: Большая российская энциклопедия, 1994. — ISBN 5-85270-087-8.
• Richard G. Milner. A Short History of Spin (англ.) // Contribution to the XVth International Workshop on Polarized Sources, Targets, and Polarimetry. — Charlottesville, Virginia, USA, September 9-13, 2013. — arXiv:1311.5016.
• Широков Ю.М., Юдин Н.П. Ядерная физика. — М.: Наука, 1972. — 672 с.
• Ширков Д. В. Физика микромира. — М.: Советская энциклопедия, 1980. — 527 с.
• Паули В. Общие принципы волновой механики. — М.: ОГИЗ, 1947. — 333 с.

Статьи

• (1949) «A precise method of determining the faraday by magnetic resonance». Physical Review 76 (12): 1877–1878. doi:10.1103/PhysRev.76.1877.2. .
• Cohen-Tannoudji, Claude. Quantum Mechanics / Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë. — 2 volume set. — John Wiley & Sons, 2006. — ISBN 978-0-471-56952-7.
• Condon, E. U. Especially Chapter 3 // The Theory of Atomic Spectra / E. U. Condon, G. H. Shortley. — Cambridge University Press, 1935. — ISBN 978-0-521-09209-8.