Список объектов, названных в честь Леонарда Эйлера
(перенаправлено с «Тождество Эйлера»)
Существует множество математических и физических объектов, названных в честь Леонарда Эйлера, что породило шуточное фольклорное правило: «В математике принято называть открытие именем второго человека, который его сделал — иначе пришлось бы всё называть именем Эйлера»[1].

Теоремы
- Теорема Эйлера в теории чисел — обобщение малой теоремы Ферма.
- Теорема вращения Эйлера — утверждение, что любое движение твёрдого тела в трёхмерном пространстве, имеющее неподвижную точку, является вращением тела вокруг некоторой оси.
- Теорема Эйлера в планиметрии — зависимость между радиусами вписанной и описанной окружностей треугольника.
- Теорема Эйлера о четырёхугольниках — связь между сторонами выпуклого четырёхугольника и его диагоналями.
- Пентагональная теорема Эйлера о производящей функции для числа разбиений.
- Гипотеза Эйлера в теории чисел — утверждение, что для любого натурального числа [math]\displaystyle{ n \gt 2 }[/math] никакую n-ю степень натурального числа нельзя представить в виде суммы из [math]\displaystyle{ (n - 1) }[/math] натуральных чисел, возведённых в [math]\displaystyle{ n }[/math]-ю степень. Опровергнуто.
- Теорема Эйлера для многогранников — связь между числом вершин, рёбер и граней многогранника. Также имеет смысл для планарного графа.
- Теорема Эйлера для однородных функций — утверждение, что дифференцируемая функция [math]\displaystyle{ f(x_1,x_2,...,x_n) }[/math] является однородной с порядком однородности [math]\displaystyle{ q }[/math], тогда и только тогда, когда выполнено соотношение Эйлера: [math]\displaystyle{ \sum x_k f'_{x_k}(x_1,x_2,...,x_n) = qf(x_1,x_2,...,x_n). }[/math]
Уравнения
- Уравнения Эйлера — Лагранжа — основные формулы вариационного исчисления, c помощью которых ищутся экстремумы функционалов, зависящих от неизвестной функции и её производной.
- Уравнения Эйлера — Пуассона — обобщение уравнения Эйлера — Лагранжа на случай, когда функционал зависит от неизвестной функции и её производных выше первого порядка.
- Уравнения Эйлера (механика твёрдого тела) — описывают вращение твердого тела.
- Уравнение Эйлера (гидродинамика) — описывает движение идеальной (невязкой) сжимаемой жидкости или газа.
- Уравнение Коши — Эйлера — линейное дифференциальное уравнение определённого типа, допускающее явное решение.
- Эйлеровы точки либрации (коллинеарные точки).
- Уравнение Эйлера — Бернулли — описывает равновесие балки.
Функции
- Функция Эйлера [math]\displaystyle{ \varphi(n) }[/math] — количество натуральных чисел, не превосходящих [math]\displaystyle{ n }[/math] и взаимно простых с ним. *:[math]\displaystyle{ \varphi(n)=n\prod_{p\mid n}\left(1-\frac{1}{p}\right),\;\;n\gt 1, }[/math]
- где [math]\displaystyle{ p }[/math] — простое число и пробегает все значения, участвующие в разложении [math]\displaystyle{ n }[/math] на простые сомножители.
- Функция Эйлера — модулярная функция [math]\displaystyle{ \phi(q)=\prod_{k=1}^\infty(1-q^k), \; |q| \le 1 }[/math]. Является классическим примером, показывающим связь между комбинаторикой и комплексным анализом.
Тождества
- Тождество Эйлера в теории чисел
- Тождество Эйлера в комплексном анализе — частный случай формулы Эйлера, связывающий пять фундаментальных чисел математики.
- Тождество Эйлера о кватернионах, «тождество Эйлера о четырёх квадратах» (алгебра) — теорема о том, что произведение сумм четырёх квадратов является суммой четырёх квадратов.
- Тождество Эйлера в алгебре многочленов — соотношение
- [math]\displaystyle{ \sum_{i=1}^{n} x_i\,\frac{\partial F}{\partial x_i} \equiv k F }[/math],
- которое справедливо для любой алгебраической формы (однородного многочлена) [math]\displaystyle{ F(x_1,\ldots,x_n) }[/math] степени [math]\displaystyle{ k }[/math].
Формулы
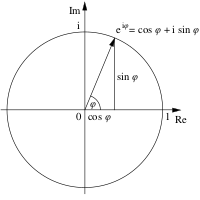
- Формула Эйлера (комплексный анализ) связывает комплексную экспоненту с тригонометрическими функциями:
- [math]\displaystyle{ e^{i x} = \cos x + i \sin x. }[/math]
- Формула Эйлера в дифференциальной геометрии:
- [math]\displaystyle{ \kappa_e=\kappa_1\cos^2\alpha+\kappa_2\sin^2\alpha }[/math],
- где [math]\displaystyle{ \kappa_e }[/math] — кривизна нормального сечения поверхности в направлении [math]\displaystyle{ e }[/math], [math]\displaystyle{ \kappa_1 }[/math] и [math]\displaystyle{ \kappa_2 }[/math] — главные кривизны (с соответствующими главными направлениями [math]\displaystyle{ e_1 }[/math] и [math]\displaystyle{ e_2 }[/math]), [math]\displaystyle{ \alpha }[/math] — угол между направлениями [math]\displaystyle{ e }[/math] и [math]\displaystyle{ e_1 }[/math].
- Формула Эйлера в кинематике связывает скорости двух точек твёрдого тела:
- [math]\displaystyle{ \vec{v}_B = \vec{v}_A + \vec{\omega}\times\vec{AB} }[/math].
- Формула Эйлера (механика трения качения в витках): [math]\displaystyle{ F = f e^{k \alpha} }[/math], связывает зависимость силы трения от числа оборотов (витков); [math]\displaystyle{ F }[/math] — сила, против которой направлено наше усилие [math]\displaystyle{ f }[/math] (наприм., подъёмная сила кранов с наматывающимся тросом), [math]\displaystyle{ e }[/math] — основание натуральных логарифмов, [math]\displaystyle{ k }[/math] — коэффициент трения между верёвкой (тросом, швартовами, талями) и наматывающей поверхностью (цилиндром-сваей, фрикционным колесом, воротом, кабестаном), [math]\displaystyle{ \alpha }[/math] — «угол навивания», то есть отношение длины дуги, охваченной верёвкой (числа оборотов), к радиусу этой дуги (см. также радиан).[2]
- Формула Эйлера для суммы первых [math]\displaystyle{ n }[/math] членов гармонического ряда.
- Формула Эйлера в теории графов, связывающая количество вершин, рёбер и граней планарного графа
- [math]\displaystyle{ |V(G)|-|E(G)|+|F(G)| = 2. }[/math]
- Формула Эйлера для треугольника — формула для расстояния между центрами вписанной и описанной окружностей треугольника.
- Формула Эйлера для четырёхугольника — выражение для расстояния между серединами диагоналей — его учетверённый квадрат равен сумме квадратов четырёх сторон четырёхугольника минус сумма квадратов двух его диагоналей. Как частный случай, из неё можно получить: тождество параллелограмма, длину медианы треугольника[3].
- Формула Эйлера для радиальных турбин и центробежных насосов
Интегралы
- Бета-функция — эйлеров интеграл (интеграл Эйлера) первого рода.
- Гамма-функция — эйлеров интеграл (интеграл Эйлера) второго рода.
- Интеграл Эйлера — Пуассона (так называемый гауссов интеграл).
Числа
- Постоянная Эйлера — Маскерони — предел разности между частичной суммой гармонического ряда и натуральным логарифмом числа.
- e (число) — основание натурального логарифма, иррациональное и трансцендентное число.
- Число Эйлера (физика) — безразмерный коэффициент, имеющий место в уравнениях Навье — Стокса, описывающий отношение между силами давления на единичный объём жидкости (или газа) и инерционными силами.
- Числа Эйлера I рода
- некорректный ISO-код «idoneal number»
- Счастливое число Эйлера
- Целое число Эйлера (Целое число Эйзенштейна)
Прочие математические понятия
- Лемма Лагранжа — Эйлера в теории цепных дробей — определение периода бесконечной цепной дроби.
- Эйлерова характеристика в алгебраической топологии — топологический инвариант.
- Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве.
- Многочлены Эйлера.
- Преобразование Эйлера — интегральное преобразование.
- Прямая Эйлера (геометрия треугольника) — прямая, проходящая через центр описанной окружности и ортоцентр треугольника.
- Окружность Эйлера, «окружность девяти точек» — в геометрии треугольника окружность, проходящая через середины всех трёх сторон треугольника.
- Круги Эйлера — геометрическая схема для отображения отношения между подмножествами.
- Критерий Эйлера, определяющий, является ли целое число квадратичным вычетом по модулю простого числа.
- Эйлеров путь (теория графов) — путь в графе, проходящий по всем рёбрам графа и притом только по одному разу. О связанных понятиях: эйлеров цикл, эйлеров граф, полуэйлеров граф см. ту же статью.
- Эйлеров сплайн — периодический идеальный сплайн минимальной нормы.
- Эйлерова сила — в механике такая сила, которая при сжимании стержня вызовет потерю его устойчивости (продольный изгиб).
- Подстановки Эйлера — замены переменных, решающие некоторые виды интегралов.
- Группа Эйлера — мультипликативная группа кольца вычетов по модулю [math]\displaystyle{ n }[/math], обозначается [math]\displaystyle{ \Z^\times_n }[/math] или [math]\displaystyle{ \Gamma(n) }[/math][4].
- Спираль Эйлера — другое название клотоиды (спирали Корню).
- Метод Эйлера — численный метод решения систем обыкновенных дифференциальных уравнений.
- Оператор Эйлера — дифференциальный оператор [math]\displaystyle{ x_1\frac{\partial f}{\partial x_1} + x_2\frac{\partial f}{\partial x_2} + \ldots + x_n\frac{\partial f}{\partial x_n} }[/math].
Прочее

- Эйлер — астероид главного пояса, открытый 29 августа 1973 года российским астрономом Тамарой Смирновой в Крымской астрофизической обсерватории.
- Эйлер — кратер ударного происхождения на видимой части Луны, диаметр 28 км.
- Олимпиада имени Леонарда Эйлера — неофициальная олимпиада, заменяющая региональный и заключительный этапы Всероссийской олимпиады школьников по математике для 8-х классов.
- Золотая медаль имени Леонарда Эйлера — награда, присуждаемая Академией наук СССР (впоследствии — Российской академии наук) за выдающиеся заслуги в математике и физике; с 1957 по 2022 год всего 8 награждённых.
- Медаль Эйлера — ежегодная награда за достижения по комбинаторике, ежегодно присуждаемая с 1993 года канадским Институтом комбинаторики и её приложений (англ. Institute of Combinatorics and its Applications).
- Медаль Эйлера — награда, присуждаемая Пермским государственным университетом за заслуги в физико-математическом образовании Пермского края.
- «Проект Эйлер» — проект в Интернете, объединяющий сотни тысяч любителей математики и программирования.
- Диск Эйлера — научная игрушка, используемая для изучения динамических систем.
- Международный математический институт имени Эйлера
- Эйлер — язык программирования, разработанный в 1965 году Никлаусом Виртом и Хельмутом Вебером, предшественник Паскаля.
- Euler — программный пакет для численных методов.
- EulerOS и OpenEuler — дистрибутивы Linux, разрабатываемые корпорацией Huawei.
- AMS Euler — шрифт, разработанный Херманом Цапфом при участии Дональда Кнута, широко используемый в документах на ΤΕΧ, в материалах Американского математического общества (AMS); впервые был использован в книге Кнута «Конкретная математика», посвящённой Эйлеру.
Примечания
- ↑ Colin Beveridge. Cracking Mathematics. — London: Cassell Illustrated; UK, 2016. — P. 215. — 499 p. — (Cracking). — ISBN 978-1844038626.
- ↑ При пеньковом канате и деревянной свае (тумбе), когда коэффициент трения [math]\displaystyle{ k }[/math] больше, усилие потребуется до смешного ничтожное, лишь бы тумба была прочной и веревка (канат) были достаточно крепкими и могли выдержать натяжение.
Перельман Я. И. Занимательная физика. в 2-х кн. Кн. 2 / Под ред. А. В. Митрофанова. — 22-е изд., стер. — М.: Наука. Гл. ред. физ.-мат. лит., 1986. — с. 35-37. — 272 с.
Ландау Л. Д., Китайгородский А. И. Физика для всех: Физические тела. — 5-е изд., испр. — М.: Наука. Главная редакция физ.-мат. литературы, 1982. — с. 31-32, 132—133. — 208 с. - ↑ Исаак Кушнир. Геометрия. Поиск и вдохновение (Геометрия на баррикадах). — Litres, 2015-11-13. — С. 306. — 593 с. — ISBN 9785457918894.
- ↑ Арнольд В. И. Группы Эйлера и арифметика геометрических прогрессий. — М. : Издательство МЦНМО, 2003. — ISBN 5-94057-141-7.