Дуга окружности
Дуга́(◡) — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой.
Если A и B — концы диаметра (то есть центральный угол AOB — развернутый), точка O — центр окружности, то они определяют две равные дуги, называемые полуокружностями. Если угол AOB не развернутый, то одна из двух дуг AB — это часть окружности, лежащая внутри угла AOB; говорят, что она меньше полуокружности, и что вторая дуга больше полуокружности. Эти углы и дуги называют дополнительными.
Дуги можно измерять в угловых единицах. Равные по центральным углам[1] дуги необязательно равны по длине и прямо пропорциональны радиусу окружности. Они равны только при равенстве радиусов окружностей.
Свойства
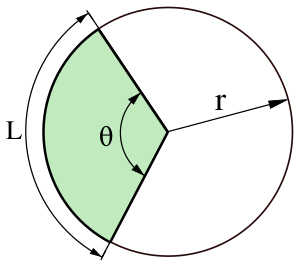
- Длина дуги [math]\displaystyle{ L }[/math] окружности радиуса [math]\displaystyle{ r }[/math] вычисляется по формуле:
- Длина хорды [math]\displaystyle{ m }[/math], стягивающей дугу окружности радиуса [math]\displaystyle{ r }[/math] с центральным углом [math]\displaystyle{ \theta }[/math]:
- [math]\displaystyle{ m = 2 r \sin\frac{\theta}{2} = 2 \frac{L}{\theta}\sin\frac{\theta}{2}. }[/math]
См. также
Примечания
- ↑ Измеренным, например, в градусах или радианах.
Ссылки
- «Углы, градусы и радианы» — перевод статьи Intuitive Guide to Angles, Degrees and Radians | BetterExplained (англ.)