Теорема Эйлера о треугольнике
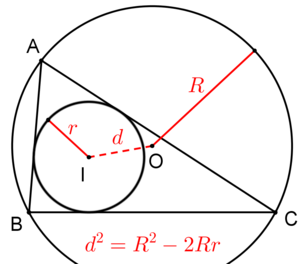
Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.
Теорема названа в честь Леонарда Эйлера.
Формулировка
Расстояние [math]\displaystyle{ d }[/math] между центрами вписанной и описанной окружностей треугольника может быть определено по формуле
- [math]\displaystyle{ d^2 = R^2 - 2Rr. }[/math]
где [math]\displaystyle{ R }[/math] — радиус описанной, [math]\displaystyle{ r }[/math] — радиус вписанной окружности.
Замечания
- Приведённую формулу можно переписать следующим образом
- [math]\displaystyle{ \frac{1}{R-d} + \frac{1}{R+d} = \frac{1}{r} }[/math].
- или
- [math]\displaystyle{ (R-r)^2=d^2+r^2, }[/math]
- Из теоремы следует так называемое неравенство Эйлера
- [math]\displaystyle{ R \ge 2r }[/math].
- Существует более сильная форма этого неравенства[1]:с. 198, а именно:
- [math]\displaystyle{ \frac{R}{r} \geq \frac{abc+a^3+b^3+c^3}{2abc} \geq \frac{a}{b}+\frac{b}{c}+\frac{c}{a}-1 \geq \frac{2}{3} \left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a} \right) \geq 2, }[/math]
- где [math]\displaystyle{ a, b, c }[/math] — стороны треугольника.
- Для сферического треугольника отношение радиуса описанной окружности к радиусу вписанной может быть меньше 2. Более того, для любого числа между 1 и 2 существует правильный сферический треугольник с отношением радиуса описанной к радиусу вписанной окружности, равным этому числу.
Доказательство
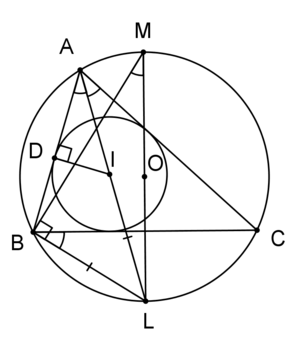
Пусть [math]\displaystyle{ O }[/math] — центр описанной окружности треугольника [math]\displaystyle{ \Delta ABC }[/math], а [math]\displaystyle{ I }[/math] — центр вписанной окружности. Если луч [math]\displaystyle{ AI }[/math] пересекает описанную окружность в точке [math]\displaystyle{ L }[/math], то [math]\displaystyle{ L }[/math] является средней точкой дуги [math]\displaystyle{ BC }[/math]. Проведём луч [math]\displaystyle{ LO }[/math] и обозначим его точку пересечения с описанной окружностью как [math]\displaystyle{ M }[/math]. Тогда [math]\displaystyle{ LM }[/math] будет диаметром описанной окружности. Из точки [math]\displaystyle{ I }[/math] опустим перпендикуляр [math]\displaystyle{ ID }[/math] на [math]\displaystyle{ AB. }[/math] Тогда [math]\displaystyle{ ID = r. }[/math] Запишем формулу Эйлера немного в другом виде
- [math]\displaystyle{ R^2 - d^2 = 2Rr. }[/math]
Можно заметить, что слева стоит степень точки [math]\displaystyle{ I }[/math] относительно описанной окружности (если быть точным, то минус степень точки). То есть, достаточно доказать равенство [math]\displaystyle{ LI \cdot IA = 2Rr }[/math]. По лемме о трезубце [math]\displaystyle{ LI = LB, }[/math] значит, достаточно доказать, что [math]\displaystyle{ LB \cdot IA = 2Rr }[/math]. Теперь заметим, что [math]\displaystyle{ 2R = LM }[/math] и [math]\displaystyle{ r = ID, }[/math] то есть, требуемое равенство можно переписать в виде [math]\displaystyle{ LB \cdot IA = LM \cdot ID. }[/math] Перепишем его ещё немного: [math]\displaystyle{ LB / LM = ID / IA }[/math]. Это равенство следует из подобия треугольников [math]\displaystyle{ \triangle AID }[/math] и [math]\displaystyle{ \triangle MLB }[/math]. В самом деле, углы [math]\displaystyle{ B }[/math] и [math]\displaystyle{ D }[/math] у этих треугольников прямые, а углы [math]\displaystyle{ A }[/math] и [math]\displaystyle{ M }[/math] равны, потому что оба опираются на дугу [math]\displaystyle{ BL }[/math] (более того, отношение [math]\displaystyle{ LB / LM = ID / IA }[/math] равно синусу угла [math]\displaystyle{ \angle BAL }[/math]).
История
Эта теорема названа в честь Леонарда Эйлера, который опубликовал её в 1765 году. Однако тот же результат был опубликован ранее Уильямом Чапплом в 1746 году.[2]
Вариации и обобщения
Для центра вневписанной окружности
Для вневписанных окружностей уравнение выглядит похоже:
- [math]\displaystyle{ (R+r_{out})^2=d^2_{out} + r_{out}^2, }[/math]
где [math]\displaystyle{ r_{out} }[/math] — радиус одной из вневписанных окружностей, а [math]\displaystyle{ d_{out} }[/math] — расстояние от центра описанной окружности до центра этой вневписанной окружности[3][4][5].
Для многоугольников

- Для радиусов [math]\displaystyle{ R }[/math] и [math]\displaystyle{ r }[/math] соответственно описанной и вписанной окружностей данного вписанно-описанного четырёхугольника (см. рис.) и расстояния [math]\displaystyle{ d=x }[/math] между центрами этих окружностей выполняется соотношение:
- [math]\displaystyle{ \frac{1}{(R+d)^2}+\frac{1}{(R-d)^2}=\frac{1}{r^2} }[/math],
- или эквивалентно,
- [math]\displaystyle{ d^2= R^2+r^2-r \sqrt {4R^2+r^2} }[/math]
- Это соотношение называют Теоремой Фусса[англ.]. Оно получено Николаем Ивановичем Фуссом[6] в 1792 году.
- Теорема Кэли о цепи Понселе обобщает теорему Эйлера на вписанно-описанные [math]\displaystyle{ n }[/math]-угольники[7].
См. также
Примечания
- ↑ Svrtan, Dragutin & Veljan, Darko (2012), Non-Euclidean versions of some classical triangle inequalities, Forum Geometricorum Т. 12: 197–209, <http://forumgeom.fau.edu/FG2012volume12/FG201217index.html> Архивная копия от 28 октября 2019 на Wayback Machine.
- ↑ Chapple, William (1746), An essay on the properties of triangles inscribed in and circumscribed about two given circles, Miscellanea Curiosa Mathematica Т. 4: 117–124, <https://archive.org/details/miscellaneacuri01unkngoog/page/n142>. The formula for the distance is near the bottom of p.123.
- ↑ Roger Nelson. Euler's triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58—61.
- ↑ R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
- ↑ Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
- ↑ Nicolas Fuss// https://en.wikipedia.org/wiki/Nicolas_Fuss Архивная копия от 17 февраля 2020 на Wayback Machine
- ↑ Авксентьев, Е. А. Инвариантные меры и теоремы о замыкании типа Понселе Архивная копия от 14 августа 2016 на Wayback Machine
Ссылки
- Weisstein, Eric W. Euler Triangle Formula (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи по математике желательно: |