Углы Эйлера

Углы Эйлера.

Анимация поочерёдного поворота сферы на углы Эйлера

Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве. Введены Леонардом Эйлером.

В сравнении с углами Эйлера кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси независимо от совершённого вращения по другим осям (см. Кватернионы и вращение пространства).

Определение

Углы Эйлера определяют три поворота системы, которые позволяют привести любое положение системы к текущему. Обозначим начальную систему координат как [math]\displaystyle{ (x, y, z) }[/math], конечную как [math]\displaystyle{ (X, Y, Z) }[/math]. Пересечение координатных плоскостей [math]\displaystyle{ xy }[/math] и [math]\displaystyle{ XY }[/math] называется линией узлов [math]\displaystyle{ N }[/math].

• Угол [math]\displaystyle{ \alpha }[/math] между осью [math]\displaystyle{ x }[/math] и линией узлов — угол прецессии.
• Угол [math]\displaystyle{ \beta }[/math] между осями [math]\displaystyle{ z }[/math] и [math]\displaystyle{ Z }[/math] — угол нутации.
• Угол [math]\displaystyle{ \gamma }[/math] между линией узлов и осью [math]\displaystyle{ X }[/math] — угол собственного вращения.

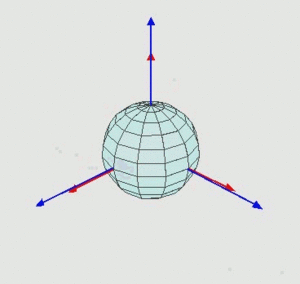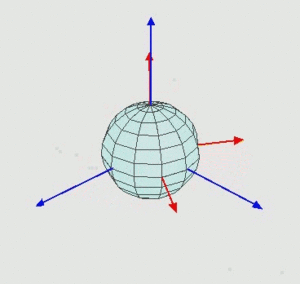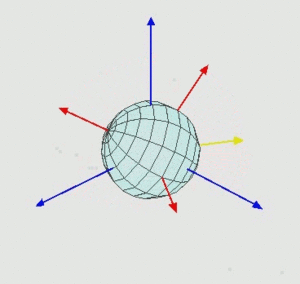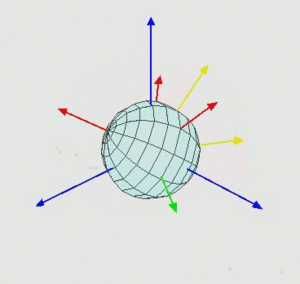
Повороты системы на эти углы называются прецессия, нутация и поворот на собственный угол (вращение). Такие повороты некоммутативны, и конечное положение системы зависит от порядка, в котором совершаются повороты. В случае углов Эйлера производится серия из трёх поворотов:

1. На угол [math]\displaystyle{ \alpha }[/math] вокруг оси [math]\displaystyle{ z }[/math]. При этом ось [math]\displaystyle{ x }[/math] переходит в [math]\displaystyle{ N }[/math].
2. На угол [math]\displaystyle{ \beta }[/math] вокруг оси [math]\displaystyle{ N }[/math]. При этом ось [math]\displaystyle{ z }[/math] переходит в [math]\displaystyle{ Z }[/math].
3. На угол [math]\displaystyle{ \gamma }[/math] вокруг оси [math]\displaystyle{ Z }[/math]. При этом ось [math]\displaystyle{ N }[/math] переходит в [math]\displaystyle{ X }[/math].

Иногда такую последовательность называют 3,1,3 (или Z,X,Z), но такое обозначение может приводить к двусмысленности.

Формулы

Углы Эйлера описывают последовательную комбинацию пассивных поворотов вокруг осей вращающейся системы координат. Матрицы этих поворотов имеют вид

[math]\displaystyle{ R_Z(\alpha) = \left( \begin{array}{ccc} \cos (\alpha ) & -\sin (\alpha ) & 0 \\ \sin (\alpha ) & \cos (\alpha ) & 0 \\ 0 & 0 & 1 \\ \end{array} \right), \quad R_X(\beta) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (\beta ) & -\sin (\beta ) \\ 0 & \sin (\beta ) & \cos (\beta ) \\ \end{array} \right), \quad R_Z(\gamma) = \left( \begin{array}{ccc} \cos (\gamma ) & -\sin (\gamma ) & 0 \\ \sin (\gamma ) & \cos (\gamma ) & 0 \\ 0 & 0 & 1 \\ \end{array} \right). }[/math]

Последовательное выполнение этих поворотов даст матрицу

[math]\displaystyle{ R = R_Z(\gamma) \cdot R_X(\beta) \cdot R_Z(\alpha) = \left( \begin{array}{ccc} \cos (\alpha ) \cos (\gamma )-\cos (\beta ) \sin (\alpha ) \sin (\gamma ) & -\cos (\gamma ) \sin (\alpha )-\cos (\alpha ) \cos (\beta ) \sin (\gamma ) & \sin (\beta ) \sin (\gamma ) \\ \cos (\beta ) \cos (\gamma ) \sin (\alpha )+\cos (\alpha ) \sin (\gamma ) & \cos (\alpha ) \cos (\beta ) \cos (\gamma )-\sin (\alpha ) \sin (\gamma ) & -\cos (\gamma ) \sin (\beta ) \\ \sin (\alpha ) \sin (\beta ) & \cos (\alpha ) \sin (\beta ) & \cos (\beta ) \\ \end{array} \right). }[/math]

Произведение [math]\displaystyle{ R \cdot \begin{pmatrix} x \\ y \\ z\end{pmatrix} }[/math], где [math]\displaystyle{ x, y, z }[/math] — координаты точки до поворота, даст координаты точки в подвижной системе координат после поворота. До и после поворота координаты точки в неподвижной системе координат неизменны.

См. также

• Список объектов, названных в честь Леонарда Эйлера
• Крен, тангаж и рыскание — угловые движения летательного аппарата или другого транспортного средства
• Матрица поворота
• Шесть степеней свободы

Литература

• Берёзкин Е. Н. Курс теоретической механики — 2-е изд., пер. — М.: Изд-во МГУ. 1974. — 641 с.
• Журавлев В. Ф. Основы теоретической механики — 2-е изд. — М.: Физматлит, 2001. С. 23.
• Уиттекер Э. Аналитическая динамика С.25