Теорема Эйлера о четырёхугольниках

Теорема Эйлера о четырёхугольниках (также закон Эйлера для четырёхугольников) — теорема планиметрии, названная в честь Леонарда Эйлера (1707—1783 гг.), которая описывает соотношение между сторонами выпуклого четырёхугольника и его диагоналями. Теорема является обобщением тождества параллелограмма, которое, в свою очередь, можно рассматривать как обобщение теоремы Пифагора; поэтому иногда используется название теорема Эйлера — Пифагора.
Теорема и специальные случаи
Для выпуклого четырёхугольника со сторонами [math]\displaystyle{ a, b, c, d }[/math] и диагоналями [math]\displaystyle{ e }[/math] и [math]\displaystyle{ f }[/math], середины которых соединены отрезком [math]\displaystyle{ g }[/math], выполняется равенство:
- [math]\displaystyle{ a^2+b^2+c^2+d^2=e^2+f^2+4g^2 }[/math]
Если четырёхугольник является параллелограммом, то средние точки диагоналей совпадают и соединяющий их отрезок [math]\displaystyle{ g }[/math] имеет длину, равную 0. Кроме того, у параллелограмма длины параллельных сторон равны, так что в таком случае теорема Эйлера сводится к формуле:
- [math]\displaystyle{ 2a^2+2b^2=e^2+f^2 }[/math]
каковая называется тождеством параллелограмма.
Если четырёхугольник является прямоугольником, то равенство ещё более упрощается, поскольку теперь две диагонали равны:
- [math]\displaystyle{ 2a^2+2b^2=2e^2 }[/math]
Деление на 2 даёт теорему Эйлера — Пифагора:
- [math]\displaystyle{ a^2+b^2=e^2 }[/math]
Другими словами: для прямоугольника отношение сторон четырёхугольника и его диагоналей описывается теоремой Пифагора[1].
Альтернативные формулировки и расширения
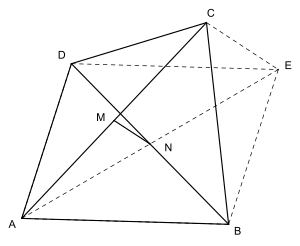
Эйлер вывел вышеописанную теорему как следствие другой теоремы, которая, с одной стороны, менее элегантна, так как требует добавления ещё одной точки, но, с другой стороны, даёт большее понимание свойств четырёхугольника.
Для заданного выпуклого четырёхугольника [math]\displaystyle{ ABCD }[/math] Эйлер ввёл дополнительную точку [math]\displaystyle{ E }[/math], такую, что [math]\displaystyle{ ABED }[/math] образует параллелограмм; тогда выполняется следующее равенство:
- [math]\displaystyle{ |AB|^2+|BC|^2+|CD|^2+|AD|^2=|AC|^2+|BD|^2+|CE|^2 }[/math]
Расстояние [math]\displaystyle{ |CE| }[/math] между дополнительной точкой [math]\displaystyle{ E }[/math] и точкой [math]\displaystyle{ C }[/math] четырёхугольника, соответствует отрезку, который не являются частью параллелограмма. Длину этого отрезка можно рассматривать как меру отличия рассматриваемого четырёхугольника от параллелограмма, или, другими словами, как меру правильности члена [math]\displaystyle{ |CE|^2 }[/math] в исходном равенстве тождества параллелограмма[2].
Поскольку точка [math]\displaystyle{ M }[/math] является серединой отрезка [math]\displaystyle{ AC }[/math], то получаем [math]\displaystyle{ \tfrac{|AC|}{|AM|}=2 }[/math]. Точка [math]\displaystyle{ N }[/math] является серединой отрезка [math]\displaystyle{ BD }[/math], и она также является серединой отрезка [math]\displaystyle{ AE }[/math], поскольку [math]\displaystyle{ AE }[/math] и [math]\displaystyle{ BD }[/math] являются диагоналями параллелограмма [math]\displaystyle{ ABED }[/math]. Отсюда получаем [math]\displaystyle{ \tfrac{|AE|}{|AN|}=2 }[/math], и, следовательно, [math]\displaystyle{ \tfrac{|AC|}{|AM|}=\tfrac{|AE|}{|AN|} }[/math]. Из теоремы Фалеса (и обратной) следует, что [math]\displaystyle{ CE }[/math] и [math]\displaystyle{ NM }[/math] параллельны. Тогда [math]\displaystyle{ |CE|^2=(2|NM|)^2=4|NM|^2 }[/math], откуда и следует теорема Эйлера[2].
Теорему Эйлера можно расширить на множество четырёхугольников, которре включает пересекающиеся и непланарные. Она выполняется для так называемых обобщённых четырёхугольников, которые состоят из четырёх произвольных точек в пространстве [math]\displaystyle{ \mathbb{R}^n }[/math], связанных рёбрами с образованием графа-цикла[3].
Примечания
- ↑ Debnath, 2010, с. 105–107.
- ↑ 2,0 2,1 Haunsperger, Kennedy, 2006, с. 137–139.
- ↑ Kandall, 2002, с. 403–404.
Литература
- Deanna Haunsperger, Stephen Kennedy. The Edge of the Universe: Celebrating Ten Years of Math Horizons. — MAA, 2006. — С. 137–139. — ISBN 9780883855553.
- Lokenath Debnath. The Legacy of Leonhard Euler: A Tricentennial Tribute. — World Scientific, 2010. — С. 105–107. — ISBN 9781848165267.
- C. Edward Sandifer. How Euler Did It. — MAA, 2007. — С. 33–36. — ISBN 9780883855638.
- Geoffrey A. Kandall. Euler's Theorem for Generalized Quadrilaterals // The College Mathematics Journal. — 2002. — Ноябрь (т. 33, № 5). — С. 403–404.
- Dietmar Herrmann. Die antike Mathematik: Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. — Springer, 2013. — С. 418. — ISBN 9783642376122.
Ссылки
- Weisstein, Eric W. Quadrilateral (англ.) на сайте Wolfram MathWorld.