Комбинаторика

Комбинато́рика — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов некоторого (чаще всего конечного) множества в соответствии с заданными правилами. Каждое такое правило определяет некоторую выборку из элементов исходного множества, которая называется комбинаторной конфигурацией. Простейшими примерами комбинаторных конфигураций^[1]^[2] являются перестановки, сочетания и размещения^[⇨].

Типичные задачи^[1] комбинаторики^[⇨]:

определить количество комбинаторных конфигураций, соответствующих заданным правилам (в частности, доказать или опровергнуть их существование);
найти практически пригодный алгоритм их полного построения;
определить свойства заданного класса комбинаторных конфигураций.

Комбинаторика тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, теорией чисел и другими^[⇨]. Она применяется в самых различных областях знаний, например, в генетике, информатике, статистике, статистической физике, лингвистике.

Термин «комбинаторика» был введён в математический обиход в 1666 году Лейбницем в труде «Рассуждения о комбинаторном искусстве».

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

Размещением из [math]\displaystyle{ n }[/math] элементов по [math]\displaystyle{ k }[/math] называется упорядоченный набор из [math]\displaystyle{ k }[/math] различных элементов некоторого [math]\displaystyle{ n }[/math]-элементного множества.
Перестановкой из [math]\displaystyle{ n }[/math] элементов (например чисел 1, 2, … [math]\displaystyle{ n }[/math]) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из [math]\displaystyle{ n }[/math] элементов по [math]\displaystyle{ n }[/math].
Сочетанием из [math]\displaystyle{ n }[/math] по [math]\displaystyle{ k }[/math] называется набор [math]\displaystyle{ k }[/math] элементов, выбранных из данных [math]\displaystyle{ n }[/math] элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа [math]\displaystyle{ n }[/math] называется всякое представление [math]\displaystyle{ n }[/math] в виде упорядоченной суммы целых положительных чисел.
Разбиением числа [math]\displaystyle{ n }[/math] называется всякое представление [math]\displaystyle{ n }[/math] в виде неупорядоченной суммы целых положительных чисел.

Примеры комбинаторных задач:

Сколько имеется способов разместить [math]\displaystyle{ n }[/math] предметов по [math]\displaystyle{ m }[/math] ящикам, чтобы выполнялись заданные ограничения?
Сколько существует функций [math]\displaystyle{ F }[/math] из [math]\displaystyle{ m }[/math]-элементного множества в [math]\displaystyle{ n }[/math]-элементное, удовлетворяющих заданным ограничениям?
Сколько существует различных перестановок из 52 игральных карт?
Ответ: 52! (52 факториал), то есть 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000,

или примерно [math]\displaystyle{ 8{,}0658 \cdot 10^{67}. }[/math]

При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?
Решение: Каждый возможный исход соответствует функции [math]\displaystyle{ F: \{1, 2\} \to \{1, 2, 3, 4, 5, 6\} }[/math] (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6 + 6 даёт нам нужный результат 12. Таким образом, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.

История

Древность и средние века

Основные комбинаторные понятия и вычислительные результаты появились в древнем мире. Классическая задача комбинаторики: «сколько есть способов извлечь [math]\displaystyle{ m }[/math] элементов из [math]\displaystyle{ N }[/math] возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.)^[3]. Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона^[3]. Во II веке до н. э. индийцы знали, что сумма всех биномиальных коэффициентов степени [math]\displaystyle{ n }[/math] равна [math]\displaystyle{ 2^n }[/math].

Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо^[4]. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.

Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло. Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000^[5]. Аристотель при изложении своей логики безошибочно перечислил все возможные типы трёхчленных силлогизмов. Аристоксен рассмотрел различные чередования длинных и коротких слогов в стихотворных размерах.^[5] Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).

В Средние века комбинаторика также продолжала развиваться, в основном, за пределами европейской цивилизации. В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. Другой индийский математик, Махавира^[en] (середина IX века), опубликовал формулы для числа перестановок и сочетаний, причём эти формулы, возможно, были знакомы индийским математикам ещё в VI веке н. э. Философ и астроном рабби Авраам ибн Эзра (около 1140 года) подсчитал число размещений с перестановками в огласовках имени Бога^[6]. Он же установил симметрию биномиальных коэффициентов. Точную формулу для них обнародовал позже талмудист и математик Леви бен Гершом (более известный как Герсонид) в 1321 году.

Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Новое время

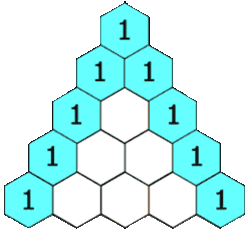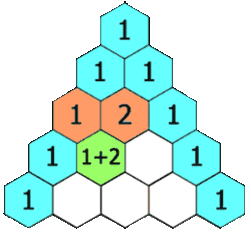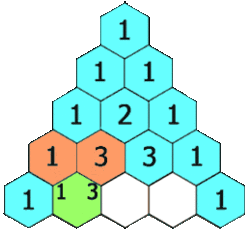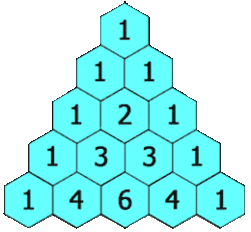
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Позднее выяснилось, что этот способ был уже известен на Востоке (примерно с X века) и он назывался арифметическим треугольником. Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Арифметический треугольник представляет собой графическую диаграмму, показывающую отношения между биномиальными коэффициентами. Позже, в средневековой Англии, кампанология^[en] предоставила примеры того, что теперь известно как гамильтоновы циклы в графах Кэли на перестановках.

В эпоху Возрождения, наряду с прочими науками, комбинаторика начала стремительное развитие. Джероламо Кардано написал проницательное математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Никколо Тарталья и Галилео Галилей. История теории вероятностей началась с переписки заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Сам термин «комбинаторика» придумал Лейбниц, он считается основоположником современной комбинаторики. В 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику^[7]. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала^[8].

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

задача о ходе коня;
задача о семи мостах, с которой началась теория графов;
построение греко-латинских квадратов;
обобщённые перестановки.

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Современное состояние

Работы Паскаля, Ньютона, Якоба Бернулли и Эйлера стали фундаментальными в развитии этой области. В наше время работы Дж. Дж. Сильвестра (конец XIX века) и Перси Макмэна^[en] (начало XX века) помогли заложить основы перечислительной и алгебраической комбинаторики. Теория графов также вызывала растущий интерес, особенно в связи с теоремой о четырёх красках и задачами экономики.

Во второй половине XX века комбинаторика пережила новый бурный рост, что было связано с быстрым развитием дискретной математики, информатики, кибернетики и планирования эксперимента. Частично этот рост был стимулирован обнаруженными связями и приложениями в других областях математики — в алгебре, теорией вероятностей, функциональном анализе, теории чисел и т. д. Эти связи стирают границы между комбинаторикой и другими областями математики, но в то же время приводят к определённой фрагментации комбинаторики.

В начале XX века началось развитие комбинаторной геометрии: были доказаны теоремы Радона, Хелли, Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана^[en]. Во второй четверти XX века были поставлены проблема Борсука и проблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

Методы и разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Числа Фибоначчи являются типичным примером задачи в перечислительной комбинаторике, а также известная Задача о письмах. Двенадцатеричный путь обеспечивает единую структуру для подсчета перестановок, сочетаний и разбиений.

Аналитическая комбинаторика

Аналитическая комбинаторика относится к перечислению комбинаторных структур с использованием инструментов из комплексного анализа и теории вероятностей. В отличие от перечислительной комбинаторики, которая использует явные комбинаторные формулы и производящие функции последовательности для описания результатов, аналитическая комбинаторика нацелена на получение асимптотических формул.

Теория разбиения

Теория разбиения изучает различные перечислительные и асимптотические задачи, связанные с разбиением натуральных чисел, и тесно связана с q-рядами, специальными функциями и ортогональными многочленами. Первоначально она была частью теории чисел и анализа, а теперь рассматривается как часть комбинаторики или самостоятельная область. Она включает в себя биективный подход, различные инструменты анализа и аналитической теории чисел, имеет также связи со статистической механикой.

Теория графов

Графы являются фундаментальными объектами в комбинаторике. Теория графов рассматривает перечисления (например, число [math]\displaystyle{ n }[/math] вершин с [math]\displaystyle{ k }[/math] рёбрами графа), существующие структуры (например, гамильтоновы циклы), алгебраические представления (например, имеет ли комбинаторное представление многочлен Татта [math]\displaystyle{ T_G(x,y) }[/math] для заданных графа [math]\displaystyle{ G }[/math] и двух чисел [math]\displaystyle{ x }[/math] и [math]\displaystyle{ y }[/math]?). Хотя между теорией графов и комбинаторикой существуют очень сильные связи, они иногда рассматриваются как отдельные предметы. В то же время комбинаторные методы применимы ко многим задачам теории графов, эти две дисциплины обычно используются для поиска решений различных типов задач.

Теория схем

Теория схем — это исследование комбинаторных схем, которые представляют собой наборы подмножеств с определёнными свойствами пересечения. Блок схемы — это комбинаторные схемы особого типа. Эта область является одной из старейших частей комбинаторики, например, предложенная в 1850 году задача Киркмана о школьницах. Решение задачи является частным случаем системы Штейнера, системы которой играют важную роль в классификации простых конечных групп. Эта область имеет дальнейшие связи с теорией кодирования и геометрической комбинаторикой.

Конечная геометрия

Конечная геометрия изучает геометрические системы с конечным числом точек. Структуры аналогичны тем, которые встречаются в непрерывной геометрии (евклидово или проективное пространство), но определены комбинаторно. Эта область является богатым источником примеров для теории схем.

Теория порядка

Теория порядка — это изучение частично упорядоченных множеств, как конечных, так и бесконечных. Различные примеры частичных порядков встречаются в алгебре, геометрии, теории чисел и во всей комбинаторике, и теории графов. Известные классы и примеры частичных порядков включают решетки и булевы алгебры.

Теория матроидов

Теория матроидов абстрагирует часть геометрии. Она изучает свойства множеств (обычно конечных множеств) векторов в векторном пространстве, которые не зависят от конкретных коэффициентов в линейно зависимом отношении. Не только структура, но и перечислительные свойства принадлежат теории матроидов. Теория матроидов была введена Хасслером Уитни и изучалась как часть теории порядка. В настоящее время это самостоятельная область исследований, имеющая ряд связей с другими разделами комбинаторики.

Экстремальная комбинаторика

Экстремальная комбинаторика изучает экстремальные вопросы о системах множеств. Типы вопросов, рассматриваемых в этом случае, относятся к самому большому возможному графу, который удовлетворяет определённым свойствам. Например, самый большой граф без треугольников на [math]\displaystyle{ 2n }[/math] вершинах — это полный двудольный граф [math]\displaystyle{ K_{n,n} }[/math]. Часто бывает слишком трудно даже точно найти экстремальный ответ^{[уточнить]} [math]\displaystyle{ f(n) }[/math] и можно дать только асимптотическую оценку.

Теория Рамсея

Теория Рамсея — это ещё одна часть экстремальной комбинаторики. Она утверждает, что любая достаточно большая конфигурация будет содержать некоторый порядок и изучает наличие регулярных структур в случайных конфигурациях элементов. Это расширенное обобщение принципа Дирихле («принцип голубей и ящиков»). Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства для случайного дискретного объекта, такого как случайный граф? Например, каково среднее число треугольников в случайном графе? Вероятностные методы также используются для определения существования комбинаторных объектов с определёнными заданными свойствами (для которых явные примеры может быть трудно найти), просто наблюдая, что вероятность случайного выбора объекта с этими свойствами больше 0. Этот подход (часто называемый вероятностным методом) доказал свою высокую эффективность в приложениях экстремальной комбинаторики и теории графов. Тесно связанной областью является изучение конечных цепей Маркова, особенно на комбинаторных объектах. Здесь снова используются вероятностные инструменты для оценки времени смешивания^[en].

Часто ассоциируемая с Палом Эрдёшем, который сделал новаторскую работу по этому предмету, вероятностная комбинаторика традиционно рассматривалась как набор инструментов для изучения задач в других частях комбинаторики. Однако с ростом приложений для анализа алгоритмов в информатике, а также классической теории вероятностей, аддитивной теории чисел и вероятностной теории чисел, эта область в последнее время выросла и стала самостоятельной областью комбинаторики.

Алгебраическая комбинаторика

Алгебраическая комбинаторика — это область математики, которая использует методы абстрактной алгебры, в частности теорию групп и теорию представлений, в различных комбинаторных контекстах и, наоборот, применяет комбинаторные методы к задачам алгебры. Алгебраическая комбинаторика постоянно расширяет свой охват, как в тематических направлениях, так и в методах и может рассматриваться как область математики, где взаимодействие комбинаторных и алгебраических методов особенно сильно и существенно.

Демонстрация создания последовательности Морса — Туэ.

Комбинаторика слов

Комбинаторика слов имеет дело с формальными языками. Она возникла самостоятельно в нескольких областях математики, в том числе в теории чисел, теории групп и теории вероятности. Она имеет приложения в перечислительной комбинаторике, фрактальном анализе^[en], теоретической информатике, теории автоматов и лингвистике. Хотя многие приложения являются новыми, классическая иерархия Хомского классов формальных грамматик является, пожалуй, самым известным результатом в этой области.

Комбинаторная геометрия

Геометрическая комбинаторика связана с выпуклой и дискретной геометрией, в частности с комбинаторикой многогранников. Например, она спрашивает, сколько граней каждого измерения может иметь выпуклый многогранник. Важную роль играют также метрические свойства многогранников, например, теорема Коши о жёсткости выпуклых многогранников. Рассматриваются также особые многогранники, такие как перестановочные многогранники, ассоциаэдры^[en] и многогранники Биркгофа. Комбинаторная геометрия — это старомодное название дискретной геометрии.

Пример ожерелья, разделённого на [math]\displaystyle{ k = 2 }[/math] (то есть между двумя участниками дележа) и [math]\displaystyle{ t = 2 }[/math] (то есть два типа бусин, имеется 8 красных и 6 зелёных). Показаны 2 разреза — один из участников получает большую секцию, а другой получает оставшиеся два куска.

Топологическая комбинаторика

Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении раскрасок графа, справедливого дележа, разбиения, дерева принятия решений, частично упорядоченных множеств, задачи о восстановлении бус и дискретной теории Морсе^[en]. Её не следует путать с комбинаторной топологией, которая является более старым названием алгебраической топологии.

Арифметическая комбинаторика

Арифметическая комбинаторика возникла из взаимодействия между теорией чисел, комбинаторикой, эргодической теории и гармоническим анализом. Она о комбинаторных оценках, связанных с арифметическими операциями (сложение, вычитание, умножение и деление). Аддитивная теория чисел (иногда также называемая аддитивной комбинаторикой) относится к частному случаю, когда задействованы только операции сложения и вычитания. Одним из важных методов арифметической комбинаторики является эргодическая теория динамических систем.

Инфинитарная комбинаторика

Инфинитарная комбинаторика^[en] — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам. Это часть теории множеств, область математической логики, но использует инструменты и идеи как теории множеств, так и экстремальной комбинаторики.

Джан-Карло Рота^[en] использовал название непрерывной комбинаторики для описания геометрической вероятности^[en], поскольку существует много аналогий между подсчетом и мерой.

Связанные области

Контактное расположение сфер связанно как теория кодирования с дискретной геометрией

Комбинаторная оптимизация

Комбинаторная оптимизация — это исследование оптимизации дискретных и комбинаторных объектов. Она начиналась как часть комбинаторики и теории графов, но теперь рассматривается как раздел прикладной математики и информатики, связанный с исследованием операций, теорией алгоритмов и теорией сложности вычислений.

Теория кодирования

Теория кодирования началась как часть теории схем с ранними комбинаторными конструкциями кодов, исправляющих ошибки. Основная идея предмета заключается в разработке эффективных и надежных методов передачи данных. Сейчас это большая область исследований, часть теории информации.

Дискретная и вычислительная геометрия

Дискретная геометрия (также называемая комбинаторной геометрией) также началась как часть комбинаторики, с ранними результатами выпуклых многогранников и контактных чисел. С появлением приложений дискретной геометрии в вычислительной геометрии, эти две области частично слились и стали отдельной областью изучения. Остается много связей с геометрической и топологической комбинаторикой, которые сами по себе можно рассматривать как порождения ранней дискретной геометрии.

Комбинаторика и динамические системы

Комбинаторные аспекты динамических систем — это ещё одна развивающаяся область. Здесь динамические системы могут быть определены комбинаторными объектами. См., например, динамическая система графов.

Комбинаторика и физика

Между комбинаторикой и физикой, в частности статистической физикой, усиливается взаимосвязь. Примеры включают точное решение модели Изинга и связь между моделью Поттса^[en] с одной стороны, и хроматическими многочленами и многочленами Татте, с другой стороны.

Открытые проблемы

Комбинаторика (в частности, теория Рамсея) содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем [math]\displaystyle{ N }[/math] в любой группе из [math]\displaystyle{ N }[/math] человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно)^[9].

Также есть и другие нерешённые задачи и недоказанные гипотезы:

Гипотеза Адамара (1893): для каждого натурального [math]\displaystyle{ n }[/math], делящегося на 4, существует вещественная матрица Адамара порядка [math]\displaystyle{ n }[/math]. Пояснение: известно, что делимость на 4 является лишь необходимым условием существования матрицы Адамара. Существуют различные методы построения вещественных матриц Адамара порядка [math]\displaystyle{ n=4k }[/math] для некоторых бесконечных серий натуральных чисел, делящихся на 4, однако они не позволяют доказать гипотезу Адамара. Наименьшим порядком, кратным 4, для которого матрица Адамара неизвестна, является [math]\displaystyle{ n=668 }[/math]^[10].
Существование конечной проективной плоскости натурального порядка, не являющегося степенью простого числа.
Гипотеза Эрдёша — Реньи. Если [math]\displaystyle{ k }[/math] — фиксированное целое число [math]\displaystyle{ k \geqslant 3 }[/math], то [math]\displaystyle{ \lim\;\inf(per(A))^{\frac{1}{n}}\gt 1 }[/math] для [math]\displaystyle{ A }[/math] из [math]\displaystyle{ \Lambda_n^k }[/math]. Здесь [math]\displaystyle{ per(A) }[/math] — перманент матрицы [math]\displaystyle{ A, \Lambda_n^k }[/math] — множество всех [math]\displaystyle{ (0,1) }[/math] — матриц порядка [math]\displaystyle{ n }[/math] c [math]\displaystyle{ k }[/math] единицами в каждой строке и каждом столбце^[11].
Числа Рамсея [math]\displaystyle{ N(q_1,q_2,...,q_t;r) }[/math] для случая [math]\displaystyle{ t\gt 2 }[/math] почти не изучены^[12].
Задача нахождения минимума перманента дважды стохастической матрицы в общем случае не решена^[13].
Не известны необходимые и достаточные условия, при которых существует общая трансверсаль для трёх семейств подмножеств^[14].

Комбинаторика в языкознании

Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.

Примечания

↑ ^1,0 ^1,1 Сачков В. Н. Комбинаторный анализ // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 974—979. — 1104 с.
↑ БРЭ.
↑ ^3,0 ^3,1 Amulya Kumar Bag. Binomial theorem in ancient India. Архивная копия от 3 августа 2021 на Wayback Machine Indian J. History Sci., 1:68-74, 1966.
↑ Виленкин Н. Я., 1975, с. 7.
↑ ^5,0 ^5,1 Виленкин Н. Я., 1975, с. 9.
↑ Краткий комментарий к Исход, 3:13.
↑ Виленкин Н. Я., 1975, с. 19.
↑ O'Connor, John; Edmund Robertson. Abraham de Moivre (неопр.). The MacTutor History of Mathematics archive. Дата обращения: 31 мая 2010. Архивировано 27 апреля 2012 года.
↑ Weisstein, Eric W. Числа Рамсея (англ.) на сайте Wolfram MathWorld.
↑ МАТРИЦЫ АДАМАРА. Архивировано 21 января 2022 года.
↑ Минк X. Перманенты.. — Мир. — 1982. — 211 с.
↑ Рыбников, 1972, с. 96.
↑ Рыбников, 1972, с. 110.
↑ Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб.: БХВ-Петербург, 2004. — С. 530. — 624 с. — ISBN 5-94157-546-7.

Литература

Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — 960 с. — ISBN 0-13-086998-8.
Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975.
Вялый М. Н. Линейные неравенства и комбинаторика. М.: МЦНМО, 2003. 32 с.
Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
Леонтьев В. К. Избранные задачи комбинаторного анализа. — М. : Изд-во МГТУ им. Н. Э. Баумана, 2001. — 179, [3] с.; 20 см; ISBN 5-7038-1862-1
Леонтьев В. К. Комбинаторика и информация : учеб. пос. … по направлению … «Прикладные математика и физика». — Москва : МФТИ, 2015. — 21 см; ISBN 978-5-7417-0518-6
Леонтьев В. К., Гордеев Э. Н. Комбинаторные аспекты теории информации. М.: МФТИ, 2019.
Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.
Райзер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
Риордан Дж. Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
Рыбников К. А. Введение в комбинаторный анализ. — М.: МГУ, 1972. — С. 96. — 308 с.
Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — 440 с. — ISBN 5-03-001348-2.
Стенли Р. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — 767 с. — ISBN 978-5-03-003476-8.

Ссылки

Белешко Д. Комбинаторика. 2004.
Комбинаторный анализ / Сачков В. Н. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Теория вероятностей. 3. Элементы комбинаторики

[ME-1] 1,0 ^1,1 Сачков В. Н. Комбинаторный анализ // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 974—979. — 1104 с.

[_9a5025601a02cea5-2] БРЭ.

[India-3] 3,0 ^3,1 Amulya Kumar Bag. Binomial theorem in ancient India. Архивная копия от 3 августа 2021 на Wayback Machine Indian J. History Sci., 1:68-74, 1966.

[_3458280f1580b0e6-4] Виленкин Н. Я., 1975, с. 7.

[V9-5] 5,0 ^5,1 Виленкин Н. Я., 1975, с. 9.

[6] Краткий комментарий к Исход, 3:13.

[_727cf1a189ac8c99-7] Виленкин Н. Я., 1975, с. 19.

[O'Connor-8] O'Connor, John; Edmund Robertson. Abraham de Moivre (неопр.). The MacTutor History of Mathematics archive. Дата обращения: 31 мая 2010. Архивировано 27 апреля 2012 года.

[9] Weisstein, Eric W. Числа Рамсея (англ.) на сайте Wolfram MathWorld.

[10] МАТРИЦЫ АДАМАРА. Архивировано 21 января 2022 года.

[11] Минк X. Перманенты.. — Мир. — 1982. — 211 с.

[_4c7d9f7a31341a6f-12] Рыбников, 1972, с. 96.

[_2dab54a19b9f8b70-13] Рыбников, 1972, с. 110.

[14] Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб.: БХВ-Петербург, 2004. — С. 530. — 624 с. — ISBN 5-94157-546-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]