Комплексный анализ

Ко́мпле́ксный ана́лиз, тео́рия фу́нкций ко́мпле́ксного переме́нного (или ко́мпле́ксной переме́нной; сокращенно — ТФКП) — раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента.

Общие понятия

Каждая комплексная функция [math]\displaystyle{ w = f(z) = f(x+iy) }[/math] может рассматриваться как пара вещественных функций от двух переменных: [math]\displaystyle{ f(z)=u(x,y)+iv(x,y), }[/math] определяющих её вещественную и мнимую часть соответственно. Функции [math]\displaystyle{ u, v }[/math] называются компонентами комплексной функции [math]\displaystyle{ f(z) }[/math].

Далее всюду, где говорится об ограниченности комплексной функции, имеется в виду ограниченность её модуля (из чего следует ограниченность в обычном смысле обеих компонент).

Понятие предела для последовательности и функции вводится так же, как и в вещественном случае, с заменой абсолютной величины на комплексный модуль. Если [math]\displaystyle{ \lim_{z\to a+bi}f(z)=A+Bi }[/math], то [math]\displaystyle{ \lim_\underset{y \to b}{x\to a}u(x,y)=A }[/math] и [math]\displaystyle{ \lim_\underset{y \to b}{x\to a}v(x,y)=B. }[/math] Верно и обратное: из существования пределов компонент вытекает существование предела самой функции, и компонентами предела будут пределы компонентов. Непрерывность комплексной функции тоже определяется так же, как в вещественном случае, и она равносильна непрерывности обеих её компонент.

Все основные теоремы о пределе и непрерывности вещественных функций имеют место и в комплексном случае, если это расширение не связано со сравнением комплексных величин на больше-меньше. Например, отсутствует прямой аналог теоремы о промежуточных значениях непрерывной функции.

[math]\displaystyle{ \varepsilon }[/math]-окрестность числа [math]\displaystyle{ z_0 }[/math] определяется как множество точек [math]\displaystyle{ z }[/math], удалённых от [math]\displaystyle{ z_0 }[/math] менее чем на [math]\displaystyle{ \varepsilon }[/math]:

[math]\displaystyle{ |z-z_0|\lt \varepsilon }[/math]

На комплексной плоскости [math]\displaystyle{ \varepsilon }[/math]-окрестность представляет собой внутренность круга радиуса [math]\displaystyle{ \varepsilon }[/math] с центром в [math]\displaystyle{ z_0 }[/math].

Бесконечно удалённая точка

В комплексном анализе часто полезно рассматривать полную комплексную плоскость, дополненную по сравнению с обычной бесконечно удалённой точкой: [math]\displaystyle{ z=\infty. }[/math] При таком подходе неограниченно возрастающая (по модулю) последовательность считается сходящейся к бесконечно удалённой точке. Алгебраические операции с бесконечностью не производятся, хотя несколько алгебраических соотношений имеют место:

• [math]\displaystyle{ \frac{z}{\infty}=0; z+\infty=\infty (z \ne \infty) }[/math]
• [math]\displaystyle{ z \cdot \infty=\infty; \frac{z}{0}=\infty (z \ne 0) }[/math]

[math]\displaystyle{ \varepsilon }[/math]-окрестностью бесконечно удалённой точки считается множество точек [math]\displaystyle{ z }[/math], модуль которых больше, чем [math]\displaystyle{ \dfrac{1}{\varepsilon} }[/math], то есть внешняя часть [math]\displaystyle{ \dfrac{1}{\varepsilon} }[/math]-окрестностей начала координат.

Дифференцирование

Определение

Производная для комплексной функции одного аргумента [math]\displaystyle{ w=f(z) }[/math] определяется так же, как и для вещественной:

[math]\displaystyle{ f'(z)=\frac{df}{dz}=\lim_{\underset{h\in\C}{h\to0}}\frac{f(z+h)-f(z)}h. }[/math]

Если этот предел существует, функция называется дифференцируемой или голоморфной. При этом

[math]\displaystyle{ f(z+h)-f(z)=\frac{df}{dz}\cdot h+o(h), }[/math] где [math]\displaystyle{ o }[/math] — «o» малое.

Следует учитывать одну важную особенность: поскольку комплексная функция задана на плоскости, существование приведённого предела означает, что он одинаков при стремлении к [math]\displaystyle{ z }[/math] с любого направления. Этот факт накладывает существенные ограничения на вид функций-компонент [math]\displaystyle{ u,\;v }[/math] и определяет их жёсткую взаимосвязь (условия Коши — Римана, они же условия Эйлера — Даламбера):

[math]\displaystyle{ \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y};\qquad\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}, }[/math]

или, если в краткой форме,

[math]\displaystyle{ \frac{\partial f}{\partial x}=\frac{\partial f}{i\partial y}. }[/math]

Отсюда следует, что дифференцируемости компонент [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] недостаточно для дифференцируемости самой функции.

Более того, имеют место следующие свойства, отличающие комплексный анализ от вещественного:

• Всякая дифференцируемая в некоторой окрестности точки [math]\displaystyle{ z }[/math] комплексная функция дифференцируема неограниченное число раз и аналитична, то есть её ряд Тэйлора сходится к данной функции во всех точках этой окрестности (в литературе наряду с термином аналитическая функция используются также его синонимы «голоморфная функция», «регулярная функция»).
• (Теорема Лиувилля): Если функция дифференцируема на всей комплексной плоскости и не является константой, то её модуль не может быть ограничен.
• Обе компоненты дифференцируемой комплексной функции являются гармоническими функциями, то есть удовлетворяют уравнению Лапласа:

[math]\displaystyle{ \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0;\qquad\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}=0. }[/math]

• Любая гармоническая функция может быть как вещественной, так и мнимой компонентой дифференцируемой функции. При этом другая компонента определяется однозначно (из условий Коши — Римана), с точностью до константы-слагаемого.

Таким образом, любая дифференцируемая комплексная функция — это функция вида [math]\displaystyle{ u+iv }[/math], где [math]\displaystyle{ u,\;v }[/math] — взаимосвязанные гармонические функции двух аргументов.

Другие свойства

Пусть функции [math]\displaystyle{ f(z) }[/math] и [math]\displaystyle{ g(z) }[/math] дифференцируемы в области [math]\displaystyle{ G\subseteq\C. }[/math] Тогда [math]\displaystyle{ f(z)\pm g(z) }[/math] и [math]\displaystyle{ f(z)\cdot g(z) }[/math] также дифференцируемы в этой области. Если [math]\displaystyle{ g(z) }[/math] в области [math]\displaystyle{ G }[/math] не обращается в ноль, то [math]\displaystyle{ \frac{f(z)}{g(z)} }[/math] будет дифференцируема в [math]\displaystyle{ G. }[/math] Композиция функций [math]\displaystyle{ f(g(z)) }[/math] дифференцируема всюду, где она определена. Если производная функции [math]\displaystyle{ w=f(z) }[/math] в области [math]\displaystyle{ G }[/math] не обращается в ноль, то существует обратная к ней функция [math]\displaystyle{ z=\varphi(w) }[/math] и она будет дифференцируема.

Производная для суммы, разности, произведения, частного от деления, композиции функций и обратной функции вычисляется по тем же формулам, что и в вещественном анализе.

Геометрический смысл производной

Пример конформного отображения. Видно, что углы сохраняются.

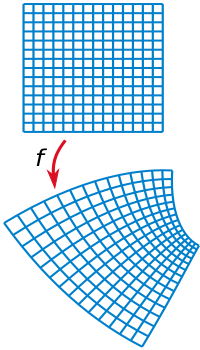
Каждая комплексная функция [math]\displaystyle{ w=f(z)=u(x,\;y)+iv(x,\;y) }[/math] определяет некоторое отображение комплексной плоскости с координатами [math]\displaystyle{ (x,\;y) }[/math] на другую комплексную плоскость с координатами [math]\displaystyle{ (u,\;v) }[/math]. При этом выражение

[math]\displaystyle{ \left|\frac{f(z+h)-f(z)}{h}\right| = k(h) }[/math]

при малом [math]\displaystyle{ h }[/math] геометрически можно истолковать как коэффициент масштабирования, которое выполняет данное отображение при переходе от точки [math]\displaystyle{ z }[/math] к точке [math]\displaystyle{ z+h }[/math]. Существование предела [math]\displaystyle{ \lim_{h \to 0} k(h) }[/math], то есть модуля производной [math]\displaystyle{ |f^\prime(z)|=k }[/math], означает, что коэффициент масштабирования одинаков в любом направлении от точки [math]\displaystyle{ z }[/math], то есть не зависит от направления. Вообще говоря, коэффициент масштабирования меняется от точки к точке.

Если коэффициент масштабирования [math]\displaystyle{ k\gt 1 }[/math], то в окрестности точки [math]\displaystyle{ z }[/math] расстояния между точками увеличиваются, и коэффициент масштабирования называют коэффициентом растяжения. Если коэффициент масштабирования [math]\displaystyle{ k\lt 1 }[/math], то в окрестности точки [math]\displaystyle{ z }[/math] расстояния между точками уменьшаются, и коэффициент масштабирования называют коэффициентом сжатия. Пример для функции [math]\displaystyle{ f(z)=z^2+2z-1 }[/math]: в точке [math]\displaystyle{ z=1 }[/math] производная равна 4, поэтому все длины увеличиваются в четыре раза.

Что касается аргумента производной, то он определяет угол поворота гладкой кривой, проходящей через данную точку [math]\displaystyle{ z }[/math]. Все гладкие кривые при таком отображении поворачиваются на один и тот же угол. Отображения, сохраняющие углы, называются конформными; таким образом, любая дифференцируемая комплексная функция определяет конформное отображение (в той области, где её производная не обращается в ноль). С этим фактом связано широкое применение комплексных функций в картографии и гидродинамике.

Интегрирование

Интегрирование комплексных функций

Понятие первообразной комплексной функции (неопределённого интеграла) вводится так же, как в вещественном случае. Однако аналог определённого интеграла в интервале от [math]\displaystyle{ a }[/math] до [math]\displaystyle{ b }[/math] на комплексной плоскости, вообще говоря, не существует, так как путь от начальной точки до конечной неоднозначен. Поэтому основным видом комплексного интеграла является криволинейный интеграл, зависящий от конкретного пути. Ниже будут указаны условия, при выполнении которых интеграл не зависит от пути, и тогда интеграл «от точки до точки» может быть определён корректно.

Пусть уравнение [math]\displaystyle{ z=z(t), }[/math] где параметр t направлен от какого-то начального значения a к конечному значению b, определяет некоторую кусочно-гладкую кривую [math]\displaystyle{ \gamma }[/math] в комплексной плоскости, наделённую направлением, а функция [math]\displaystyle{ f(z) }[/math] определена в точках этой кривой. Направление, в котором движется параметр, определяет конкретный обход кривой: при этом неважно, что́ больше — b или a. Разделим отрезок параметризации на [math]\displaystyle{ n }[/math] равных частей [math]\displaystyle{ t_0,t_1\cdots t_{n-1},t_n\colon }[/math]

• [math]\displaystyle{ a=t_0\lt t_1\lt \ldots\lt t_n=b, }[/math] если a < b;
• или [math]\displaystyle{ a=t_0\gt \ldots\gt t_n=b, }[/math] если a > b,

и рассмотрим интегральную сумму:

[math]\displaystyle{ \sum_{k=1}^nf\big(z(t_k)\big)\cdot\big(z(t_k)-z(t_{k-1})\big). }[/math]

Предел этой суммы при неограниченном возрастании [math]\displaystyle{ n }[/math] называется (комплексным) интегралом по (направленной) кривой [math]\displaystyle{ \gamma }[/math] от данной функции [math]\displaystyle{ f(z) }[/math]; он обозначается:

[math]\displaystyle{ \int_\gamma f(z)dz. }[/math]

Для любой функции [math]\displaystyle{ f(z) }[/math], непрерывной вдоль [math]\displaystyle{ \gamma }[/math], этот интеграл существует и может быть вычислен через обычный вещественный интеграл по параметру:

[math]\displaystyle{ \int_\gamma f(z)dz=\int_a^bf(z(t))z'(t)dt=\int_\gamma(u~dx-v~dy)+i\int_\gamma(v~dx+u~dy). }[/math]

Здесь [math]\displaystyle{ u,\;v }[/math] — компоненты [math]\displaystyle{ f(z) }[/math]. Из этого представления можно заметить, что свойства комплексного интеграла аналогичны свойствам вещественного криволинейного интеграла второго рода.

Контурный интеграл

Особый практический интерес представляют интегралы по (замкнутому) контуру, то есть по кусочно-гладкой кривой без точек самопересечения, у которой начальная точка совпадает с конечной. Контур можно обходить в двух направлениях; положительным считается направление, при котором ограниченная контуром область располагается слева по ходу движения.

Если кривая [math]\displaystyle{ \gamma }[/math] образует замкнутый контур, употребляется особое обозначение интеграла:

[math]\displaystyle{ \oint_\gamma f(z)dz. }[/math]

Иногда стрелочкой на кружке указывают направление: по часовой стрелке или против.

Имеет место важная интегральная теорема Коши: для любой функции [math]\displaystyle{ f(z) }[/math], аналитической в односвязной области [math]\displaystyle{ A\subseteq\C, }[/math] и для любого замкнутого контура [math]\displaystyle{ \gamma\subseteq A }[/math] интеграл по нему равен нулю:

[math]\displaystyle{ \oint_\gamma f(z)dz=0{.} }[/math]

Следствие: пусть функция [math]\displaystyle{ f(z) }[/math] аналитична в односвязной области [math]\displaystyle{ A\subseteq\C, }[/math] а точки [math]\displaystyle{ z_1, z_2 }[/math] из области [math]\displaystyle{ A }[/math] соединены некоторой кривой [math]\displaystyle{ \gamma }[/math]. Тогда интеграл [math]\displaystyle{ \textstyle\int_\gamma f(z)dz }[/math] зависит только от точек [math]\displaystyle{ z_1, z_2 }[/math], но не от выбора соединяющей их кривой [math]\displaystyle{ \gamma }[/math], так что можно обозначить его [math]\displaystyle{ \textstyle\int\limits_{z_1}^{z_2}f(z)dz. }[/math]

Если выполнены условия теоремы Коши, то можно ввести понятие неопределённого интеграла для [math]\displaystyle{ f(z) }[/math]. Для этого зафиксируем внутри области некоторую точку [math]\displaystyle{ z_0 }[/math] и рассмотрим интеграл:

[math]\displaystyle{ F(z) = \int_{z_0}^z{f(w)dw}. }[/math]

Производная [math]\displaystyle{ F'(z) }[/math] равна [math]\displaystyle{ f(z) }[/math], поэтому [math]\displaystyle{ F(z) }[/math] — первообразная для [math]\displaystyle{ f(z). }[/math] Семейство первообразных, различающихся константой (зависящей от выбора [math]\displaystyle{ z_0 }[/math]), образует неопределённый интеграл. Имеет место теорема Ньютона — Лейбница:

[math]\displaystyle{ \int_{z_1}^{z_2} {f(z)\,dz} = F(z_2) - F(z_1). }[/math]

Существует обобщение интегральной теоремы Коши для многосвязной области: если функция аналитична в замкнутой многосвязной области, то интеграл от неё по внешнему контуру области равен сумме интегралов по всем внутренним контурам (в том же направлении, что и по внешнему). Это обобщение удобно применять, если область содержит особую точку функции (определение особой точки ниже), где функция не аналитична или не определена.

Другие мощные инструменты для исследования комплексных и вещественных интегралов:

• интегральная формула Коши и её следствия: принцип максимума модуля, теоремы о среднем;
• основная теорема о вычетах.

Теоремы единственности и аналитическое продолжение

Нулём функции [math]\displaystyle{ f(z) }[/math] называется точка [math]\displaystyle{ z_0 }[/math], в которой функция обращается в ноль: [math]\displaystyle{ f(z_0)=0 }[/math].

Теорема о нулях аналитической функции. Если нули функции [math]\displaystyle{ f(z) }[/math], аналитической в области [math]\displaystyle{ D }[/math], имеют предельную точку внутри [math]\displaystyle{ D }[/math], то функция [math]\displaystyle{ f(z) }[/math] всюду в [math]\displaystyle{ D }[/math] равна нулю.

Следствие: если функция [math]\displaystyle{ f(z) }[/math] аналитична в области [math]\displaystyle{ D }[/math] и не равна тождественно нулю в ней, то в любой ограниченной замкнутой подобласти [math]\displaystyle{ C\subseteq D }[/math] у неё может быть лишь конечное число нулей.

Теорема единственности аналитической функции. Пусть [math]\displaystyle{ \{z_n\} }[/math] — бесконечная сходящаяся последовательность различных точек области [math]\displaystyle{ D. }[/math] Если две аналитические функции [math]\displaystyle{ f(z), g(z) }[/math] совпадают во всех точках этой последовательности, то они тождественно равны в [math]\displaystyle{ D. }[/math]

В частности, если две аналитические функции совпадают на некоторой кусочно-гладкой кривой в [math]\displaystyle{ D }[/math], то они совпадают всюду в [math]\displaystyle{ D }[/math]. Это значит, что значения аналитической функции даже на небольшом участке области полностью определяют поведение функции во всей области её определения. Задав аналитическую функцию на кривой (например, на вещественной оси), мы однозначно определяем её расширение (если оно возможно) на более широкую область, которое называется аналитическим продолжением исходной функции.

Все стандартные функции анализа — многочлен, дробно-линейная функция, степенная функция, экспонента, тригонометрические функции, обратные тригонометрические функции, логарифм — допускают аналитическое продолжение на комплексную плоскость. При этом для их аналитических продолжений будут иметь место те же алгебраические, дифференциальные и другие тождества, что и для вещественного оригинала, например:

[math]\displaystyle{ \sin^2 z + \cos^2 z = 1; \qquad e^u \cdot e^v = e^{u+v}. }[/math]

Разложение в ряд

Степенной ряд

Определение суммы числового ряда и признаки сходимости в комплексном анализе практически такие же, как в вещественном, с заменой абсолютной величины на комплексный модуль; исключение составляют признаки сходимости, в которых происходит сравнение на больше-меньше самих элементов ряда, а не их модулей.

Всякая дифференцируемая в точке [math]\displaystyle{ z_0 }[/math] функция разлагается в окрестности этой точки в степенной ряд Тейлора:

[math]\displaystyle{ f(z) = \sum_{n=0}^\infty a_n(z-z_0)^n }[/math]

Коэффициенты ряда вычисляются по обычным формулам. Этот ряд сходится к функции [math]\displaystyle{ f(z) }[/math] в некотором круге радиуса [math]\displaystyle{ R }[/math] с центром в точке [math]\displaystyle{ z_0 }[/math], который служит аналогом интервала сходимости вещественного ряда. В этом круге ряд абсолютно сходится, а вне его расходится. При этом возможны 3 случая.

1. Ряд сходится в круге конечного и ненулевого радиуса.
2. Ряд сходится во всей комплексной плоскости, то есть [math]\displaystyle{ R=\infty }[/math]. Такие функции называются целыми.
3. Ряд сходится только в точке [math]\displaystyle{ z_0 }[/math]. Пример: [math]\displaystyle{ \sum_{n=0}^\infty n! (z-z_0)^n }[/math]. Такие точки [math]\displaystyle{ z_0 }[/math] называются особыми для функции [math]\displaystyle{ f(z). }[/math] Неособые точки называются правильными. Внутренность круга сходимости состоит из правильных точек.

Граница круга сходимости содержит хотя бы одну особую точку. Отсюда следует, что радиус круга сходимости в точке [math]\displaystyle{ z_0 }[/math] равен расстоянию от [math]\displaystyle{ z_0 }[/math] до ближайшей к ней особой точки.

Теорема Абеля: если [math]\displaystyle{ R }[/math] — радиус круга сходимости степенного ряда, то в любом круге с тем же центром, но меньшего радиуса, ряд сходится равномерно.

Ряд Лорана

Представляет большой практический интерес исследование поведения функции вблизи изолированной особой точки, то есть точки, в окрестности которой функция аналитична, но в самой точке либо не аналитична, либо не определена. Степенной ряд здесь бесполезен, поэтому вводится более общий ряд Лорана:

[math]\displaystyle{ \sum_{n=-\infty}^{\infty}c_n(z-z_0)^n = \sum_{n=0}^{\infty}c_n(z-z_0)^n + \sum_{n=1}^{\infty} \frac {c_{-n}} {(z-z_0)^n} }[/math]

Если область сходимости ряда Лорана не пуста, она представляет собой круговое кольцо: [math]\displaystyle{ r\lt |z-z_0|\lt R }[/math].

Основная теорема: если функция [math]\displaystyle{ f(z) }[/math] аналитична в круговом кольце, то она может быть представлена в этом кольце сходящимся рядом Лорана, причём однозначно.

Как и для степенного ряда, границы кольца сходимости определяются распределением особых точек функции. По виду ряда Лорана можно сделать некоторые выводы о поведении функции вблизи точки [math]\displaystyle{ z_0 }[/math].

1. Устранимая особая точка: если ряд Лорана не содержит элементов с отрицательными степенями [math]\displaystyle{ z-z_0 }[/math]. Тогда это просто степенной ряд, определяющий функцию в некотором круге, окружающем [math]\displaystyle{ z_0 }[/math]. Сумма ряда в этом круге конечна и может отличаться от [math]\displaystyle{ f(z) }[/math] только в точке [math]\displaystyle{ z_0 }[/math], так что достаточно переопределить [math]\displaystyle{ f(z_0) }[/math], чтобы функция стала аналитичной во всём круге. Имеет место следующий признак: если функция вблизи [math]\displaystyle{ z_0 }[/math] аналитична и ограничена, то [math]\displaystyle{ z_0 }[/math] — устранимая особая точка.
2. Полюс: если ряд Лорана содержит конечное число элементов с отрицательными степенями [math]\displaystyle{ z-z_0 }[/math]. В этом случае функция в точке [math]\displaystyle{ z_0 }[/math] бесконечна (по модулю).
3. Существенно особая точка: если ряд Лорана содержит бесконечное число элементов с отрицательными степенями [math]\displaystyle{ z-z_0 }[/math]. В этом случае функция в точке [math]\displaystyle{ z_0 }[/math] не может быть корректно определена так, чтобы быть непрерывной.

Приложения в вещественном анализе

С помощью теории вычетов, являющейся частью ТФКП, вычисляются многие сложные интегралы по замкнутым контурам.

Средствами комплексного анализа объясняются некоторые моменты, не поддающиеся простой интерпретации в терминах вещественного анализа. Приведём классический пример: функция

[math]\displaystyle{ f(x)=\frac{1}{1+x^2} }[/math]

непрерывна и бесконечно дифференцируема на всей вещественной прямой. Рассмотрим её ряд Тейлора

[math]\displaystyle{ \frac{1}{1+x^2}=1-x^2+x^4-x^6+\ldots }[/math]

Этот ряд сходится только в интервале [math]\displaystyle{ (-1;\;1) }[/math], хотя точки [math]\displaystyle{ \pm 1 }[/math] не являются какими-то особенными для [math]\displaystyle{ f(x) }[/math].

Положение проясняется при переходе к функции комплексного переменного [math]\displaystyle{ f(z)=\frac{1}{1+z^2} }[/math], у которой обнаруживаются две особые точки: [math]\displaystyle{ \pm i }[/math]. Соответственно, эту функцию можно разложить в ряд Тейлора только в круге [math]\displaystyle{ \Delta=\{z\colon|z|\lt 1\} }[/math].

История

См. также: Комплексное число § История

Фундаментальные работы в комплексном анализе связаны с именами Эйлера, Римана, Коши, Вейерштрасса и многих других известных математиков. Теория конформных отображений стала бурно развиваться благодаря имеющимся применениям в инженерном деле, методы и результаты комплексного анализа применяются в аналитической теории чисел. Новый всплеск интереса к комплексному анализу связан с комплексной динамикой и теорией фракталов.

См. также

• Аналитическая функция
• Вычет (комплексный анализ)
• Голоморфная функция
• Кватернионный анализ
• Комплексные числа
• Многомерный комплексный анализ
• Моногенная функция
• Проективно расширенная числовая прямая — одномерный аналог комплексной плоскости, дополненной беззнаковой бесконечно удалённой точкой.

Литература

• Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М.: Наука, 1968. — 472 с.
• Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Краснов М. Л., Киселев А. И., Макаренко Г. И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. — М.: Наука, 1981. — 304 с.
• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд. — М.: Наука, 1972.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
• Смирнов В. И. Курс высшей математики в трёх томах. — Изд. 10-е. — СПб.: БХВ-Петербург, 2010. — Т. 3, часть 2-я. — 816 с. — ISBN 978-5-9775-0087-6.
• Титчмарш Е. Теория функций: Пер. с англ. — 2-е изд., перераб. — М.: Наука, 1980. — 464 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — М.: Физматлит, 2001. — ISBN 5-9221-0155-2.
• Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.