Первообразная

Первообрáзная для функции [math]\displaystyle{ f(x) }[/math] (иногда называемая антипроизводной или примити́вной функцией) — это такая функция, производная которой равна [math]\displaystyle{ f(x) }[/math]. Это одно из важнейших понятий математического анализа вещественной переменной (существуют также обобщения этого понятия для комплексных функций^[1]).

Определение

Первообразной для данной функции [math]\displaystyle{ f(x) }[/math] называют^[2] такую функцию [math]\displaystyle{ F(x) }[/math], производная которой равна [math]\displaystyle{ f }[/math] (на всей области определения [math]\displaystyle{ f }[/math]), то есть [math]\displaystyle{ F'(x) = f(x) }[/math]. Нахождение первообразной является операцией, обратной дифференцированию — последнее по заданной функции находит её производную, а найдя первообразную, мы, наоборот, по заданной производной определили исходную функцию.

Первообразные важны тем, что позволяют вычислять определённые интегралы. Если [math]\displaystyle{ F }[/math] — первообразная интегрируемой непрерывной функции [math]\displaystyle{ f }[/math], то:

[math]\displaystyle{ \int\limits_a^b f(x)\, dx = F(b) - F(a). }[/math]

Это соотношение называется формулой Ньютона — Лейбница.

Технически нахождение первообразной заключается в вычислении неопределённого интеграла для [math]\displaystyle{ f(x) }[/math], а сам процесс называется интегрированием. О применении этой теории в геометрии см. Интегральное исчисление.

Пример: функция [math]\displaystyle{ F(x) = \frac{x^3}{3} }[/math] является первообразной для [math]\displaystyle{ f(x) = x^2, }[/math] потому что [math]\displaystyle{ F'(x)=f(x). }[/math]

Неоднозначность

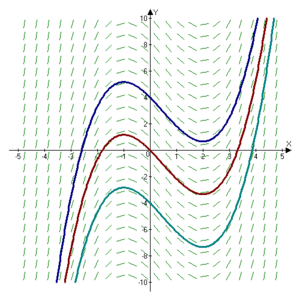
Если [math]\displaystyle{ F }[/math] — первообразная для [math]\displaystyle{ f }[/math], то любая функция, полученная из [math]\displaystyle{ F }[/math] добавлением константы: [math]\displaystyle{ G(x) = F(x) + C }[/math] тоже является первообразной для [math]\displaystyle{ f }[/math]. Таким образом, если функция имеет первообразную, то она входит в целое семейство первообразных^[2] [math]\displaystyle{ F(x) + C, }[/math] которое называется неопределённым интегралом [math]\displaystyle{ f(x) }[/math] и записывается в виде интеграла без указания пределов:

[math]\displaystyle{ \int f(x)\, dx }[/math]

Верно и обратное: если [math]\displaystyle{ F }[/math] — первообразная для [math]\displaystyle{ f }[/math], и функция [math]\displaystyle{ f }[/math] определена на каком-либо интервале, тогда каждая первообразная [math]\displaystyle{ G }[/math] отличается от [math]\displaystyle{ F }[/math] на константу: всегда существует число [math]\displaystyle{ C }[/math], такое что [math]\displaystyle{ G(x) = F(x) + C }[/math] для всех [math]\displaystyle{ x }[/math]. Графики таких первообразных смещены вертикально относительно друг друга посредством параллельного переноса, и их положение зависит от значения [math]\displaystyle{ C. }[/math] Число [math]\displaystyle{ C }[/math] называют постоянной интегрирования.

Например, семейство первообразных для функции [math]\displaystyle{ x^2 }[/math] имеет вид: [math]\displaystyle{ F(x) = \frac{x^3}{3}+C }[/math], где [math]\displaystyle{ C }[/math] — любое число.

Если область определения функции [math]\displaystyle{ f }[/math] не является сплошным интервалом, то её первообразные не обязаны отличаться на константу^[3]. Так, например, функция [math]\displaystyle{ \frac{1}{x^2} }[/math] не существует в нуле, поэтому её область определения состоит из двух интервалов: [math]\displaystyle{ x\gt 0 }[/math] и [math]\displaystyle{ x\lt 0. }[/math] Соответственно получаются два независимых семейства первообразных на этих интервалах: [math]\displaystyle{ -\frac{1}{x}+\hat C }[/math], где [math]\displaystyle{ \hat C }[/math] является константой при [math]\displaystyle{ x\gt 0 }[/math] и, вообще говоря, другой константой при [math]\displaystyle{ x\lt 0 }[/math]:

[math]\displaystyle{ \hat C (x) = \left\{ \begin{aligned} C_1, \text{ если } x\lt 0\\ C_2, \text{ если } x\gt 0 \end{aligned} \right. }[/math]

Существование

Каждая непрерывная функция [math]\displaystyle{ f }[/math] имеет первообразную [math]\displaystyle{ F }[/math], одна из которых представляется в виде интеграла от [math]\displaystyle{ f }[/math] с переменным верхним пределом:

[math]\displaystyle{ F(x) = \int\limits_a^x f(t)\,dt. }[/math]

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, [math]\displaystyle{ f(x) = 2x\sin\frac{1}{x}-\cos\frac{1}{x} }[/math] с [math]\displaystyle{ f(0) = 0 }[/math] не непрерывна при [math]\displaystyle{ x = 0 }[/math], но имеет первообразную [math]\displaystyle{ F(x) = x^2 sin\frac{1}{x} }[/math] с [math]\displaystyle{ F(0) = 0 }[/math]. Для разрывных ограниченных функций вместо интеграла Римана удобно использовать более общий интеграл Лебега. Необходимыми условиями существования первообразной являются принадлежность функции [math]\displaystyle{ f }[/math] первому классу Бэра и выполнение для неё свойства Дарбу^[2].

Многие первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (то есть через многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

[math]\displaystyle{ \int e^{-x^2}\,dx,\qquad \int \frac{\sin(x)}{x}\,dx,\qquad \int\frac{1}{\ln x}\,dx }[/math].

Для таких функций интеграл от них, если он существует, может быть вычислен приближённо с помощью численного интегрирования.

Свойства первообразной

Первообразная суммы функций равна сумме первообразных для слагаемых.
Первообразная произведения константы и функции равна произведению константы и первообразной функции.
У всех функций, непрерывных на отрезке, существуют и первообразная, и интеграл по Риману. Однако в общем случае существование первообразной и интегрируемость функции не связаны^[4]:
- Функция знака (sgn) интегрируема по Риману, но не имеет первообразной (из-за разрыва в нуле).
- У функции [math]\displaystyle{ f(x)=x^2 \sin\frac{1}{x^2} }[/math] (положим также [math]\displaystyle{ f(0)=0 }[/math]) на отрезке [math]\displaystyle{ [-1,1] }[/math] имеется конечная производная [math]\displaystyle{ g(x); }[/math] таким образом, у функции [math]\displaystyle{ g(x) }[/math] существует первообразная (а именно, [math]\displaystyle{ f(x) }[/math]), но [math]\displaystyle{ g(x) }[/math] не ограничена на [math]\displaystyle{ [-1,1] }[/math] и поэтому не интегрируема по Риману.

Техника интегрирования

Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

линейность интегрирования позволяет разбивать сложные интегралы на части,
интегрирование подстановкой, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
интегрирование по частям для операций с произведениями функций,
метод обратной цепочки, особый случай интегрирования по частям,
метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
алгоритм Риша - алгоритм для интегрирования любых элементарных функций,
некоторые интегралы можно найти в таблицах, см. Категория:Списки интегралов,
при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символьные операции (в частности алгоритм Риша), что очень удобно, когда алгебраические вычисления становятся слишком громоздкими.

Примечания

↑ Первообразная функции комплексных переменных (неопр.). Дата обращения: 7 мая 2019. Архивировано 7 мая 2019 года.
↑ ^2,0 ^2,1 ^2,2 Первообразная // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 237.
↑ Шибинский, 2007, с. 139—140.
↑ Гелбаум, Б., Олмстед, Дж. Контрпримеры в анализе = Counterexamples in Analysis. — М.: ЛКИ, 2007. — С. 57, 51. — 258 с. — ISBN 978-5-382-00046-6.

Литература

Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — 872 с.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966. — Т. 2. — 800 с.
Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — 543 с. — ISBN 978-5-06-005774-4.

Ссылки

Wolfram Integrator — вычисление интегралов онлайн с помощью системы Mathematica
Mathematical Assistant on Web — символьные вычисления онлайн Архивная копия от 1 декабря 2008 на Wayback Machine
Онлайн Калькулятор Интегралов Архивная копия от 6 января 2010 на Wayback Machine

[1] Первообразная функции комплексных переменных (неопр.). Дата обращения: 7 мая 2019. Архивировано 7 мая 2019 года.

[ME-2] 2,0 ^2,1 ^2,2 Первообразная // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 237.

[_9a042cb3be7b28cf-3] Шибинский, 2007, с. 139—140.

[4] Гелбаум, Б., Олмстед, Дж. Контрпримеры в анализе = Counterexamples in Analysis. — М.: ЛКИ, 2007. — С. 57, 51. — 258 с. — ISBN 978-5-382-00046-6.

[1]

[2]

[3]

[4]