Степенная функция
Степенна́я фу́нкция — функция [math]\displaystyle{ y=x^a }[/math], где [math]\displaystyle{ a }[/math] (показатель степени) — некоторое вещественное число[1][2]. К степенным часто относят и функцию вида [math]\displaystyle{ y=kx^a }[/math], где [math]\displaystyle{ k }[/math] — некоторый (ненулевой) коэффициент[3]. Существует также комплексное обобщение степенной функции.
Степенная функция является частным случаем многочлена. На практике показатель степени почти всегда является целым или рациональным числом.
Вещественная функция
Область определения
Для целых положительных показателей [math]\displaystyle{ a }[/math] степенную функцию можно рассматривать на всей числовой прямой, тогда как для отрицательных [math]\displaystyle{ a }[/math], функция не определена в нуле (нуль является её особой точкой)[4].
Для рациональных [math]\displaystyle{ a=\frac{p}{q}\ (q\gt 0) }[/math] область определения зависит от чётности [math]\displaystyle{ q }[/math] и от знака [math]\displaystyle{ p. }[/math] так как [math]\displaystyle{ x^a = \sqrt[q]{x^p}. }[/math]:
- Если [math]\displaystyle{ q }[/math] нечётно и [math]\displaystyle{ p\gt 0 }[/math], то [math]\displaystyle{ x^{p/q} }[/math] определён на всей числовой прямой.
- Если [math]\displaystyle{ q }[/math] нечётно и [math]\displaystyle{ p\lt 0 }[/math], то [math]\displaystyle{ x^{p/q} }[/math] определён на всей числовой прямой, кроме нуля.
- Если [math]\displaystyle{ q }[/math] чётно и [math]\displaystyle{ p\gt 0 }[/math], то [math]\displaystyle{ x^{p/q} }[/math] определён при неотрицательных [math]\displaystyle{ x. }[/math]
- Если [math]\displaystyle{ q }[/math] чётно и [math]\displaystyle{ p\lt 0 }[/math], то [math]\displaystyle{ x^{p/q} }[/math] определён при положительных [math]\displaystyle{ x. }[/math]
Для вещественного показателя [math]\displaystyle{ a }[/math] степенная функция [math]\displaystyle{ x^a }[/math], вообще говоря, определена только при [math]\displaystyle{ x\gt 0. }[/math] Если [math]\displaystyle{ a\gt 0, }[/math] то функция определена и в нуле[4].
Целочисленный показатель степени
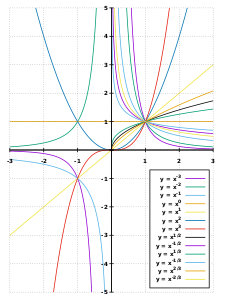
Графики степенной функции [math]\displaystyle{ y=x^n }[/math] при целочисленном показателе [math]\displaystyle{ n }[/math]:
-
Параболы порядка n: [math]\displaystyle{ n=0 }[/math] [math]\displaystyle{ n=1 }[/math] [math]\displaystyle{ n=2 }[/math] [math]\displaystyle{ n=3 }[/math] [math]\displaystyle{ n=4 }[/math] [math]\displaystyle{ n=5 }[/math] -
Гиперболы порядка n: [math]\displaystyle{ n=-1 }[/math] [math]\displaystyle{ n=-2 }[/math] [math]\displaystyle{ n=-3 }[/math]
При нечётном [math]\displaystyle{ n }[/math] графики центрально-симметричны относительно начала координат, в котором имеет точку перегиба. При чётном [math]\displaystyle{ n }[/math] степенная функция чётна: [math]\displaystyle{ (-x)^n = x^n, }[/math] её график симметричен относительно оси ординат[5].
Графики степенной функции при натуральном показателе [math]\displaystyle{ n\gt 1 }[/math] называются параболами порядка [math]\displaystyle{ n }[/math]. При чётном [math]\displaystyle{ n }[/math] функция всюду неотрицательна (см. графики). При [math]\displaystyle{ n=1 }[/math] получается функция [math]\displaystyle{ y=kx }[/math], называемая линейной функцией или прямой пропорциональной зависимостью[3][5].
Графики функций вида [math]\displaystyle{ y=x^{-n} = \frac{1}{x^n} }[/math], где [math]\displaystyle{ n }[/math] — натуральное число, называются гиперболами порядка [math]\displaystyle{ n }[/math]. При нечётном [math]\displaystyle{ n }[/math] оси координат являются асимптотами гипербол. При чётном [math]\displaystyle{ n }[/math] асимптотами являются ось абсцисс и положительное направление оси ординат (см. графики)[6]. При показателе [math]\displaystyle{ -1 }[/math] получается функция [math]\displaystyle{ y=\frac {k}{x} }[/math], называемая обратной пропорциональной зависимостью[3][5].
При [math]\displaystyle{ a=0 }[/math] функция вырождается в константу: [math]\displaystyle{ y=1. }[/math]
Рациональный показатель степени
-
Графики степенных функций с рациональным показателем
-
Полукубические параболы [math]\displaystyle{ y=ax^{3/2} }[/math]
Возведение в рациональную степень [math]\displaystyle{ p/q }[/math] определяется формулой:
- [math]\displaystyle{ x^{p/q} = \sqrt[q]{x^p}. }[/math]
Если [math]\displaystyle{ p=1 }[/math], то функция представляет собой арифметический корень степени [math]\displaystyle{ q }[/math]:
- [math]\displaystyle{ y=x^{1/q} = \sqrt[q]x. }[/math]
Пример: из третьего закона Кеплера непосредственно вытекает, что период [math]\displaystyle{ T }[/math] обращения планеты вокруг Солнца связан с большой полуосью [math]\displaystyle{ A }[/math] её орбиты соотношением: [math]\displaystyle{ T=kA^{3/2} }[/math] (полукубическая парабола).
Свойства
Монотонность
В интервале [math]\displaystyle{ (0, \infty) }[/math] функция монотонно возрастает при [math]\displaystyle{ a\gt 0 }[/math] и монотонно убывает при [math]\displaystyle{ a\lt 0. }[/math] Значения функции в этом интервале положительны[3].
Аналитические свойства
Функция непрерывна и неограниченно дифференцируема во всех точках, в окрестности которых она определена[4].
Производная функции: [math]\displaystyle{ \left( x^a \right)^\prime = a x^{a-1} }[/math].
Ноль, вообще говоря, является особой точкой. Так, если [math]\displaystyle{ a \lt n }[/math], то [math]\displaystyle{ n }[/math]-я производная в нуле не определена. Например, функция [math]\displaystyle{ y=\sqrt{x} = x^{1/2} }[/math] определена в нуле и в его правой окрестности, но её производная [math]\displaystyle{ y=\frac{1}{2\sqrt{x}} }[/math] в нуле не определена.
- Если [math]\displaystyle{ a \ne -1 }[/math], то [math]\displaystyle{ \int x^a dx = \frac{x^{a+1}}{a+1} + C }[/math]
- При [math]\displaystyle{ a = -1 }[/math] получаем: [math]\displaystyle{ \int \frac {1} {x} dx = \ln |x| + C }[/math]
Таблица значений малых степеней
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1296 | 7776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Комплексная функция
Степенная функция комплексного переменного [math]\displaystyle{ z }[/math] в общем виде определяется формулой[7]:
- [math]\displaystyle{ y=z^c=e^{c \cdot \operatorname{Ln} (z)} }[/math]
Здесь показатель степени [math]\displaystyle{ c }[/math] — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма, называется главным значением степени. Например, значение [math]\displaystyle{ i^i }[/math] равно [math]\displaystyle{ e^{-(4 k+1)\frac{\pi}{2}}, }[/math] где [math]\displaystyle{ k }[/math] — произвольное целое, а его главное значение есть [math]\displaystyle{ e^{i\ln(i)}=e^{-\frac{\pi}{2}}. }[/math]
Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.
- При натуральном показателе степени функция [math]\displaystyle{ y=z^n }[/math] однозначна и n-листна[8].
- Если показатель степени — положительное рациональное число, то есть (несократимая) дробь [math]\displaystyle{ \frac{p}{q} }[/math], то у функции будет [math]\displaystyle{ q }[/math] различных значений[7].
См. также
Примечания
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, §48: Важнейшие классы функций..
- ↑ Выгодский М. Я. Справочник по элементарной математике. М.: Наука,1978. Стр. 312.
- ↑ Перейти обратно: 3,0 3,1 3,2 3,3 Математическая энциклопедия, 1985.
- ↑ Перейти обратно: 4,0 4,1 4,2 4,3 БРЭ.
- ↑ Перейти обратно: 5,0 5,1 5,2 Математический энциклопедический словарь, 1988.
- ↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — изд. 13-е. — М.: Наука, 1985. — С. 171—172. — 544 с.
- ↑ Перейти обратно: 7,0 7,1 Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том II, стр. 526-527..
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — С. 88. — 304 с.
Литература
- Битюцков В. И. Степенная функция // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 208—209. — 1248 с.
- Степенная функция // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 564—565. — 847 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — изд. 6-е. — М.: Наука, 1966.
Ссылки
- Степенная функция // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
![Параболы порядка n: [math]\displaystyle{ n=0 }[/math] [math]\displaystyle{ n=1 }[/math] [math]\displaystyle{ n=2 }[/math] [math]\displaystyle{ n=3 }[/math] [math]\displaystyle{ n=4 }[/math] [math]\displaystyle{ n=5 }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Puissance_enti%C3%A8re.svg&width=250)
![Гиперболы порядка n: [math]\displaystyle{ n=-1 }[/math] [math]\displaystyle{ n=-2 }[/math] [math]\displaystyle{ n=-3 }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Puissance_inverse.svg&width=250)
![Полукубические параболы [math]\displaystyle{ y=ax^{3/2} }[/math]](https://cdn.xn--h1ajim.xn--p1ai/thumb.php?f=Neil-parab-3.svg&width=216)