Теория категорий

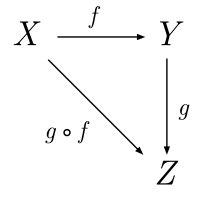
Тео́рия катего́рий — раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов.

Теория категорий занимает центральное место в современной математике^[1], она также нашла применения в информатике^[2], логике^[3] и в теоретической физике^[4]^[5]. Современное изложение алгебраической геометрии и гомологической алгебры существенно опирается на понятия теории категорий. Общекатегорийные понятия также активно используются в языке функционального программирования Haskell^[6]. Была создана Саундерсом Маклейном и Самуэлем Эйленбергом.

Определение

Категория [math]\displaystyle{ \mathcal{C} }[/math] — это:

класс объектов [math]\displaystyle{ \mathrm{Ob}_{\mathcal{C}} }[/math];
для каждой пары объектов [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] задано множество морфизмов (или стрелок) [math]\displaystyle{ \mathrm{Hom}_{\mathcal{C}}(A,B) }[/math], причём каждому морфизму соответствуют единственные [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math];
для пары морфизмов [math]\displaystyle{ f\in \mathrm{Hom}(A,B) }[/math] и [math]\displaystyle{ g\in \mathrm{Hom}(B,C) }[/math] определена композиция [math]\displaystyle{ g\circ f\in \mathrm{Hom}(A,C) }[/math];
для каждого объекта [math]\displaystyle{ A }[/math] задан тождественный морфизм [math]\displaystyle{ \mathrm{id}_A\in \mathrm{Hom}(A,A) }[/math];

причём выполняются две аксиомы:

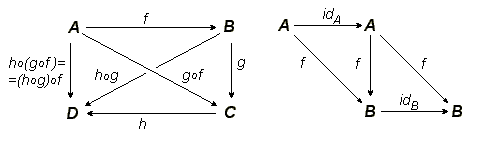
операция композиции ассоциативна: [math]\displaystyle{ h\circ(g\circ f) = (h\circ g)\circ f }[/math] и
тождественный морфизм действует тривиально: [math]\displaystyle{ f\circ \mathrm{id}_A = \mathrm{id}_B\circ f = f }[/math] для [math]\displaystyle{ f\in \mathrm{Hom}(A,B) }[/math]

Малая категория

Класс объектов не обязательно является множеством в смысле аксиоматической теории множеств. Категория [math]\displaystyle{ \mathcal{C} }[/math], в которой [math]\displaystyle{ \mathrm{Ob}_{\mathcal{C}} }[/math] является множеством и [math]\displaystyle{ \mathrm{Hom}(\mathcal{C}) }[/math] (совокупность всех морфизмов категории) является множеством, называется малой. Кроме того, возможно (с небольшим исправлением определения) рассмотрение категорий, в которых морфизмы между любыми двумя объектами также образуют класс или даже большую структуру^[7]. В этом варианте определения категория, в которой морфизмы между двумя зафиксированными объектами образуют множество, называется локально малой.

Примеры категорий

Set — категория множеств. Объектами в этой категории являются множества, морфизмами — отображения множеств.
Grp — категория групп. Объектами являются группы, морфизмами — отображения, сохраняющие групповую структуру (гомоморфизмы групп).
Vect_K — категория векторных пространств над полем K. Морфизмы — линейные отображения.
Категория модулей.

Аналогично определяются категории для других алгебраических систем.

Top — категория топологических пространств. Морфизмы — непрерывные отображения.
Для любого частично упорядоченного множества можно построить малую категорию, объектами которой являются элементы множества, причём между элементами x и y существует единственный морфизм тогда и только тогда, когда x≤y (разумеется, следует отличать эту категорию от категории частично упорядоченных множеств!).
Met — категория, объектами которой являются метрические пространства, а морфизмами — короткие отображения.

Коммутативные диаграммы

Стандартным способом описания утверждений теории категорий являются коммутативные диаграммы. Коммутативная диаграмма — это ориентированный граф, в вершинах которого находятся объекты, а стрелками являются морфизмы, причём результат композиции стрелок не зависит от выбранного пути. Например, аксиомы теории категорий (ассоциативность композиции и свойство тождественного морфизма) можно записать с помощью диаграмм:

Двойственность

Для категории [math]\displaystyle{ \mathcal{C} }[/math] можно определить двойственную категорию [math]\displaystyle{ \mathcal{C}^{op} }[/math], в которой:

объекты совпадают с объектами исходной категории;
морфизмы получаются «обращением стрелок»: [math]\displaystyle{ \mathrm{Hom}_{\mathcal{C}^{op}}(B,A) \simeq \mathrm{Hom}_{\mathcal{C}}(A,B) }[/math]

Принцип двойственности гласит, что для любого утверждения теории категорий можно сформулировать двойственное утверждение с помощью обращения стрелок, при этом истинность утверждения не изменится. Часто двойственное понятие обозначается тем же термином с приставкой ко- (см. примеры дальше).

Основные определения и свойства

Изоморфизм, эндоморфизм, автоморфизм

Морфизм [math]\displaystyle{ f\in \mathrm{Hom}(A,B) }[/math] называется изоморфизмом, если существует такой морфизм [math]\displaystyle{ g \in \mathrm{Hom}(B,A) }[/math], что [math]\displaystyle{ g\circ f = \mathrm{id}_A }[/math] и [math]\displaystyle{ f\circ g = \mathrm{id}_B }[/math]. Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.

Морфизмы, в которых начало и конец совпадают, называют эндоморфизмами. Множество эндоморфизмов [math]\displaystyle{ \mathrm{End}(A) = \mathrm{Hom}(A,A) }[/math] является моноидом относительно операции композиции с единичным элементом [math]\displaystyle{ \mathrm{id}_A }[/math].

Эндоморфизмы, которые одновременно являются изоморфизмами, называются автоморфизмами. Автоморфизмы любого объекта образуют группу автоморфизмов [math]\displaystyle{ \mathrm{Aut}(A) }[/math] по композиции.

Мономорфизм, эпиморфизм, биморфизм

Мономорфизм — это морфизм [math]\displaystyle{ f\in \mathrm{Hom}(A,B) }[/math] такой, что для любых [math]\displaystyle{ g_1,g_2\in \mathrm{Hom}(X,A) }[/math] из [math]\displaystyle{ f\circ g_1 = f\circ g_2 }[/math] следует, что [math]\displaystyle{ g_1=g_2 }[/math]. Композиция мономорфизмов есть мономорфизм.

Эпиморфизм — это такой морфизм [math]\displaystyle{ f\in \mathrm{Hom}(A,B) }[/math], что для любых [math]\displaystyle{ g_1,g_2\in \mathrm{Hom}(B,X) }[/math] из [math]\displaystyle{ g_1\circ f = g_2\circ f }[/math] следует [math]\displaystyle{ g_1=g_2 }[/math]. Композиция эпиморфизмов есть эпиморфизм.

Биморфизм — это морфизм, являющийся одновременно мономорфизмом и эпиморфизмом. Любой изоморфизм есть биморфизм, но не любой биморфизм есть изоморфизм.

Мономорфизм, эпиморфизм и биморфизм являются обобщениями понятий инъективного, сюръективного и биективного отображения соответственно. Любой изоморфизм является мономорфизмом и эпиморфизмом, обратное, вообще говоря, верно не для всех категорий.

Инициальный и терминальный объекты

Инициальный (начальный, универсально отталкивающий) объект категории — это такой объект, из которого в любой объект категории существует единственный морфизм.

Если инициальные объекты в категории существуют, то все они изоморфны.

Двойственным образом определяется терминальный или универсально притягивающий объект — это такой объект, в который из любого объекта категории существует единственный морфизм.

Объект категории называется нулевым, если он одновременно инициальный и терминальный.

Пример: В категории Set инициальным объектом является пустое множество [math]\displaystyle{ \varnothing }[/math], терминальным — любое множество из одного элемента [math]\displaystyle{ \{\cdot\} }[/math].

Пример: В категории Grp существует нулевой объект — это группа из одного элемента.

Произведение и сумма объектов

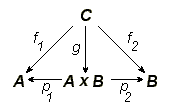
Произведение (пары) объектов A и B — это объект [math]\displaystyle{ A\times B }[/math] с морфизмами [math]\displaystyle{ p_1: A\times B\to A }[/math] и [math]\displaystyle{ p_2: A\times B \to B }[/math] такими, что для любого объекта [math]\displaystyle{ C }[/math] с морфизмами [math]\displaystyle{ f_1: C\to A }[/math] и [math]\displaystyle{ f_2: C\to B }[/math] существует единственный морфизм [math]\displaystyle{ g: C \to A\times B }[/math] такой, что диаграмма, изображённая справа, коммутативна. Морфизмы [math]\displaystyle{ p_1: A\times B\to A }[/math] и [math]\displaystyle{ p_2: A\times B \to B }[/math] называются проекциями.

Двойственно определяется сумма или копроизведение [math]\displaystyle{ A+B }[/math] объектов [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math]. Соответствующие морфизмы [math]\displaystyle{ \imath_A: A\to A+B }[/math] и [math]\displaystyle{ \imath_B: B \to A+B }[/math] называются вложениями. Несмотря на своё название, в общем случае они могут и не быть мономорфизмами.

Если произведение и копроизведение существуют, то они определяются однозначно с точностью до изоморфизма.

Пример: В категории Set произведение A и B — это прямое произведение в смысле теории множеств [math]\displaystyle{ A\times B }[/math], а сумма — дизъюнктное объединение [math]\displaystyle{ A \sqcup B }[/math].

Пример: В категории колец Ring сумма — это тензорное произведение [math]\displaystyle{ A\otimes B }[/math], а произведение — прямая сумма колец [math]\displaystyle{ A\oplus B }[/math].

Пример: В категории Vect_K (конечные) произведение и сумма изоморфны — это прямая сумма векторных пространств [math]\displaystyle{ A\oplus B }[/math].

Несложно определить аналогичным образом произведение любого семейства объектов [math]\displaystyle{ \prod_{i\in I} A_i }[/math]. Бесконечные произведения устроены в общем случае гораздо сложнее, чем конечные. Например, в то время как конечные произведения и копроизведения в Vect_K изоморфны прямым суммам, бесконечные произведения и копроизведения не являются изоморфными. Элементами бесконечного произведения [math]\displaystyle{ \prod_{i\in I} V_i }[/math] являются произвольные бесконечные последовательности элементов [math]\displaystyle{ v_i \in V_i }[/math], в то время как элементами бесконечного копроизведения [math]\displaystyle{ \coprod_{i\in I} V_i }[/math] являются последовательности, в которых лишь конечное число членов — ненулевые.

Функторы

Функторы — это отображения категорий, сохраняющие структуру. Точнее,

(Ковариантный) функтор [math]\displaystyle{ \mathcal{F}: \mathcal{C}\to \mathcal{D} }[/math] ставит в соответствие каждому объекту категории [math]\displaystyle{ \mathcal{C} }[/math] объект категории [math]\displaystyle{ \mathcal{D} }[/math] и каждому морфизму [math]\displaystyle{ f: A\to B }[/math] морфизм [math]\displaystyle{ F(f): \mathcal{F}(A)\to \mathcal{F}(B) }[/math] так, что

[math]\displaystyle{ F(\mathrm{id}_A) = \mathrm{id}_{F(A)} }[/math] и
[math]\displaystyle{ F(g)\circ F(f) = F(g\circ f) }[/math].

Контравариантный функтор, или кофунктор можно понимать как ковариантный функтор из [math]\displaystyle{ \mathcal{C} }[/math] в [math]\displaystyle{ \mathcal{D}^{op} }[/math] (или из [math]\displaystyle{ \mathcal{C}^{op} }[/math] в [math]\displaystyle{ \mathcal{D} }[/math]), то есть «функтор, переворачивающий стрелки». А именно, каждому морфизму [math]\displaystyle{ f: A\to B }[/math] он сопоставляет морфизм [math]\displaystyle{ F(f): \mathcal{F}(B)\to \mathcal{F}(A) }[/math], соответственным образом обращается правило композиции: [math]\displaystyle{ F(g)\circ F(f) = F(f\circ g) }[/math].

Естественные преобразования

Понятие естественного преобразования выражает связь между двумя функторами. Функторы часто описывают «естественные конструкции», в этом смысле естественные преобразования описывают «естественные морфизмы» таких конструкций.

Если [math]\displaystyle{ F }[/math] и [math]\displaystyle{ G }[/math] — ковариантные функторы из категории [math]\displaystyle{ C }[/math] в [math]\displaystyle{ D }[/math], то естественное преобразование [math]\displaystyle{ \eta }[/math] сопоставляет каждому объекту [math]\displaystyle{ X }[/math] категории [math]\displaystyle{ C }[/math] морфизм [math]\displaystyle{ \eta_X: F(X)\to G(X) }[/math] таким образом, что для любого морфизма [math]\displaystyle{ f:X\to Y }[/math] в категории [math]\displaystyle{ C }[/math] следующая диаграмма коммутативна:

Два функтора называются естественно изоморфными, если между ними существует естественное преобразование, такое что [math]\displaystyle{ \eta_X }[/math] — изоморфизм для любого [math]\displaystyle{ X }[/math].

Некоторые типы категорий

См. также

Примечания

↑ Хелемский, 2004.
↑ Rydeheard, Burstall, 1988.
↑ Голдблатт, 1983.
↑ Родин, 2010.
↑ Иванов.
↑ Category theory in Haskell.
↑ J. Adámek, H. Herrlich, G. E. Strecker Abstract and concrete categories: The joy of cats Архивная копия от 25 марта 2010 на Wayback Machine, — New York: John Wiley and Sons, — 1990.

Ссылки

«Category Theory» in Stanford Encyclopedia of Philosophy (англ.).
И. Иванов. Нужна ли физикам теория категорий? (рус.). Элементы (10 сентября 2008).
Category theory in Haskell (англ.). Дата обращения: 13 марта 2011. Архивировано 23 августа 2011 года.

Литература

С. Мак Лейн [Maclane S.] Категории для работающего математика (рус.). — Москва: Физматлит, 2004.
С. Мак Лейн [Maclane S.] Гомология (рус.). — Москва: Мир, 1966. — Т. 114. — (Springer-Verlag — Grundlehren der mathematischen wissenschaften).
Цаленко М. С., Шульгейфер Е. Г. Категории (рус.). — 1969. — Т. 06. — (ВИНИТИ — Итоги науки и техники, Алгебра-Топология-Геометрия).
Цаленко М. С., Шульгейфер Е. Г. Лекции по теории категорий (рус.). — Москва: Наука, 1970.
Цаленко М. С., Шульгейфер Е. Г. Основы теории категорий (рус.). — Москва: Наука, 1974.
Букур И., Деляну А. Введение в теорию категорий и функторов (рус.). — Москва: Мир, 1972. — С. 259.
Фейс [Faith C.] том 1 // Алгебра — кольца, модули и категории (рус.). — Москва: Мир, 1977. — Т. 190. — (Springer-Verlag — Grundlehren der mathematischen wissenschaften).
Фейс [Faith C.] том 2 // Алгебра — кольца, модули и категории (рус.). — Москва: Мир, 1977. — Т. 191. — (Springer-Verlag — Grundlehren der mathematischen wissenschaften).
Габриель [Gabriel P.], Цисман [Zisman M.] Категории частных и теория гомотопий (рус.). — Москва: Мир, 1977. — Т. 35. — (Springer-Verlag — Grundlehren der mathematischen wissenschaften).
Голдблатт [Goldblatt R.] Топосы — категорный анализ логики (рус.). — 1983. — Т. 98. — (Studies in logic & foundation of mathematics).
Фултон Е, Мак-Фёрсон Р. Категорный подход к изучению пространств с особенностями (рус.) / под ред. Бухштабер В. М.. — 1983. — Т. 33. — (Новое в зарубежной науке, математика).
Артамонов В. А., Салий В. Н., Скорняков Л. А., Шеврин Л. Н., Шульгейфер Е. Г. Общая алгебра (рус.). — Москва: Наука, 1991. — Т. 2. — 480 с. — (Новое в зарубежной науке, математика). — 25 500 экз. — ISBN 5-02-014427-4.
D. E. Rydeheard, R. M. Burstall. Computational Category Theory (англ.). — New York: Prentice Hall, 1988. — 257 p. — ISBN 0-13-162736-8.
Хелемский А. Я. Лекции по функциональному анализу (рус.). — Москва: МЦНМО, 2004. — ISBN 5-94057-065-8.
Р. Голдблатт. Топосы. Категорный анализ логики = Topoi. The categorial analysis of logic (рус.). — Москва: Мир, 1983. — 488 с.
Родин А. В. Теория категорий и поиски новых математических оснований физики // Вопросы философии. — 2010. — № 7. — С. 67.

[_dae02a400d1e3032-1] Хелемский, 2004.

[_63c98735a1c0f146-2] Rydeheard, Burstall, 1988.

[_6775d5c777cdf25c-3] Голдблатт, 1983.

[_b94476fe0b854d21-4] Родин, 2010.

[_620169fcff6260c0-5] Иванов.

[_2d3961fa53bff25d-6] Category theory in Haskell.

[JoyOfCats-7] J. Adámek, H. Herrlich, G. E. Strecker Abstract and concrete categories: The joy of cats Архивная копия от 25 марта 2010 на Wayback Machine, — New York: John Wiley and Sons, — 1990.

[1]

[2]

[3]

[4]

[5]

[6]

[7]