Базис

Ба́зис (др.-греч. βάσις «основа») — упорядоченный (конечный или бесконечный) набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора. Векторы базиса называются базисными векторами.

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

• Базис Га́меля (англ. Hamel basis), в определении которого рассматриваются только конечные линейные комбинации; применяется в основном в абстрактной алгебре.
• Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды; применяется в основном в функциональном анализе, в частности, для гильбертова пространства.

В конечномерных пространствах оба определения базиса совпадают.

Происхождение термина

У Евклида и других древнегреческих математиков слово «базис» (βάσις, в значении основание) обозначало горизонтальное основание плоской или пространственной фигуры. Современный математический смысл этому термину придал Дедекинд в статье 1885 года.

Базис на плоскости и в трёхмерном пространстве

Базис на плоскости. Базисные векторы изображены голубым и оранжевым цветом, зелёный вектор может быть представлен в виде суммы базисных векторов, умноженных на некоторые коэффициенты (зелёный = −2 голубой + 1 оранжевый), называемой линейной комбинацией и, таким образом, линейно зависим от них, как и любой другой вектор этого пространства (плоскости), каждый из которых тоже может быть представлен в виде линейной комбинации голубого и оранжевого с какими-то коэффициентами.

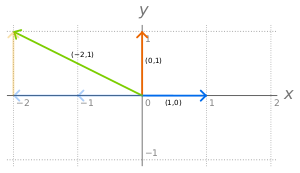
Любой декартовой системе координат на плоскости или в трёхмерном пространстве (также и в пространстве другой размерности) может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).

Часто удобно выбрать длину (норму) каждого из базисных векторов единичной, такой базис называется нормированным.

Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным.

В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).

Обозначения

Обозначение векторов базиса может быть в принципе произвольным. Часто используют какую-нибудь букву с индексом (числовым или совпадающим с названием координатной оси), например:

[math]\displaystyle{ \vec e_1, \vec e_2 }[/math]

или

[math]\displaystyle{ \vec e_x, \vec e_y }[/math]

— типичные обозначения базиса двумерного пространства (плоскости),

Декартовы координаты в трёхмерном пространстве (левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Базисом, соответствующим такой системе координат, является тройка векторов, каждый из которых направлен вдоль какой-то из осей (три базисных вектора изображаются исходящими из общего начала).

[math]\displaystyle{ \vec e_1, \vec e_2, \vec e_3 }[/math]

или

[math]\displaystyle{ \vec e_x, \vec e_y, \vec e_z }[/math]

— трёхмерного пространства. Для трёхмерного пространства часто по традиции используется и обозначение

[math]\displaystyle{ \vec i, \vec j, \vec k. }[/math]

Представление какого-то конкретного (любого) вектора [math]\displaystyle{ \vec a }[/math] пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например

[math]\displaystyle{ \vec a = a_x\vec e_x + a_y\vec e_y + a_z\vec e_z }[/math]

или

[math]\displaystyle{ \vec a = a_1\vec e_1 + a_2\vec e_2 + a_3\vec e_3 }[/math]

или, употребляя знак суммы [math]\displaystyle{ \Sigma }[/math]:

[math]\displaystyle{ \vec a = \sum_{i=1}^3 a_i\vec e_i }[/math]

называется разложением этого вектора по этому базису.

Числовые коэффициенты [math]\displaystyle{ (a_x,a_y,a_z) }[/math] называются коэффициентами разложения, а их набор в целом — представлением (или представителем) вектора [math]\displaystyle{ \vec a }[/math] в базисе [math]\displaystyle{ \vec e_x, \vec e_y, \vec e_z. }[/math] (Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор).

Виды базисов

Базис Гамеля

Базис Га́меля — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации (полнота базиса), и такое представление для любого вектора единственно.

Критерием единственности решения задачи разложения вектора по полной системе векторов является линейная независимость векторов, входящих в полную систему. Линейная независимость означает, что всякая линейная комбинация векторов системы, в которой хотя бы один коэффициент ненулевой, имеет ненулевую сумму. То есть это эквивалентно единственности разложения нулевого вектора.

В случае линейных пространств, когда всякий ненулевой коэффициент обратим, линейная независимость эквивалентна невозможности выразить какой-либо вектор полной системы линейной комбинацией остальных векторов. (В более общей ситуации — модулей над кольцами — эти два свойства неэквивалентны). Невозможность выразить никакой вектор базиса через остальные означает минимальность базиса как полной системы векторов — при удалении любого из них теряется полнота.

В вопросе о существовании базисов основной является следующая лемма (доказательство этой леммы в общем случае неконструктивно и использует аксиому выбора):

Лемма. Пусть [math]\displaystyle{ S_1 }[/math] — полная, а [math]\displaystyle{ S_2 }[/math] — линейно независимая система векторов. Тогда система [math]\displaystyle{ S_1 }[/math] содержит набор векторов, дополняющий [math]\displaystyle{ S_2 }[/math] до базиса пространства [math]\displaystyle{ V }[/math].

Доказательство

Доказательство строится на применении леммы Цорна. Рассмотрим [math]\displaystyle{ S=S_1\cup S_2 }[/math]. Пусть [math]\displaystyle{ L }[/math] — множество всех линейно независимых подмножеств [math]\displaystyle{ S }[/math]. Это множество частично упорядочено по отношению включения.

Докажем, что объединение любой цепи линейно независимых множеств остаётся линейно независимым. Действительно, возьмём вектора [math]\displaystyle{ a_1,\ldots,a_n }[/math] из объединения и возьмём множества из цепи, которым эти вектора принадлежат: [math]\displaystyle{ a_1\in A_1,\ldots,a_n\in A_n }[/math]. Так как эти множества — элементы цепи, их объединение даст максимальное из них, которое линейно независимо, а значит и вектора [math]\displaystyle{ a_1,\ldots,a_n }[/math], лежащие в этом множестве, также линейно независимы.

Объединение множеств цепи линейно независимо, а значит, содержится в множестве [math]\displaystyle{ L }[/math]. Применим к нему усиленную формулировку леммы Цорна, которая утверждает, что для каждого элемента из [math]\displaystyle{ L }[/math] есть максимальный элемент больший или равный ему. [math]\displaystyle{ S_2\in L }[/math], а значит, есть такой максимальный элемент [math]\displaystyle{ B\in L }[/math], что [math]\displaystyle{ S_2\subset B }[/math]. Легко видеть, что [math]\displaystyle{ B }[/math] есть базис. Действительно, не будь [math]\displaystyle{ B }[/math] полной системой векторов, был бы вектор [math]\displaystyle{ a\in S_1 }[/math], непредставимый как линейная комбинация векторов из [math]\displaystyle{ B }[/math]. Тогда [math]\displaystyle{ B\cup\{a\} }[/math] — линейно независимая система, а значит, [math]\displaystyle{ B\cup\{a\}\in L }[/math], что противоречит тому, что [math]\displaystyle{ B }[/math] —— максимальный элемент [math]\displaystyle{ L }[/math].

Следствием этой леммы являются утверждения:

1. Каждое линейное пространство обладает базисом.
2. Базис пространства можно выделить из любой полной системы векторов.
3. Всякую линейно независимую систему можно дополнить до базиса пространства V.

Любые два базиса в линейном пространстве равномощны, так что мощность базиса — величина, независящая от выбора базисных векторов. Она называется размерностью пространства (обозначается [math]\displaystyle{ \dim V }[/math]). Если линейное пространство имеет конечный базис, его размерность конечна и оно называется конечномерным, в противном случае его размерность бесконечна, и пространство называется бесконечномерным.

Выбранный базис линейного пространства позволяет ввести координатное представление векторов, чем подготавливается использование аналитических методов.

Линейное отображение из одного линейного пространства в другое однозначно определено, если задано на векторах какого-нибудь базиса. Комбинация этого факта с возможностью координатного представления векторов предопределяет применение матриц для изучения линейных отображений векторных пространств (в первую очередь — конечномерных). При этом многие факты из теории матриц получают наглядное представление и приобретают весьма содержательный смысл, когда они выражены на языке линейных пространств. И выбор базиса при этом служит хоть и вспомогательным, но в то же время ключевым средством.

Примеры

• Векторы [math]\displaystyle{ e_1, e_2,\dots,e_n }[/math] пространства [math]\displaystyle{ \R^n }[/math] образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0: [math]\displaystyle{ \det\{e_1, e_2,\dots,e_n\} \neq 0 }[/math].
• В пространстве всех многочленов над полем один из базисов составляют степенные функции: [math]\displaystyle{ 1, x, x^2,\dots,x^n,\dots }[/math].
• Понятие базиса используется в бесконечномерном случае, например вещественные числа образуют линейное пространство над рациональными числами и оно имеет континуальный базис Гамеля и, соответственно, континуальную размерность.

Базис Гамеля и разрывная линейная функция

Базис Гамеля может быть использован для построения разрывной вещественной функции, удовлетворяющей условию [math]\displaystyle{ f(x+y)=f(x)+f(y) }[/math]. Пусть [math]\displaystyle{ \{r_\alpha\} }[/math] — базис Гамеля множества действительных чисел [math]\displaystyle{ \mathbb{R} }[/math] над полем рациональных чисел [math]\displaystyle{ \mathbb{Q} }[/math]. Тогда для каждого [math]\displaystyle{ x = k_{\alpha_1} r_{\alpha_1} + \cdots + k_{\alpha_n} r_{\alpha_n} }[/math] ([math]\displaystyle{ k_i \in \mathbb{Q} }[/math]) положим [math]\displaystyle{ f(x) = k_{\alpha_1} f_{\alpha_1} + \cdots + k_{\alpha_n} f_{\alpha_n} }[/math], где [math]\displaystyle{ f_{\alpha_n} = f(r_{\alpha_n}) }[/math] произвольные вещественные числа, например, рациональные (в этом случае функция [math]\displaystyle{ f(x) }[/math] принимает лишь рациональные значения и тем самым гарантированно не является линейной функцией [math]\displaystyle{ f(x) = (c \cdot x) }[/math]). Такая функция [math]\displaystyle{ f(x) }[/math] аддитивна, то есть удовлетворяет функциональному уравнению Коши [math]\displaystyle{ f(x+y)=f(x)+f(y) }[/math]. Однако в общем случае, когда [math]\displaystyle{ f_{\alpha_n} \neq c \cdot r_{\alpha_n} }[/math], она отличается от линейной функции [math]\displaystyle{ f(x) = c \cdot x }[/math] и в силу этого является разрывной в любой точке, а также не сохраняет знак, не ограничена ни сверху, ни снизу, не монотонна, не интегрируема и не измерима на любом сколь угодно малом интервале, заполняя своими значениями на этом интервале всюдо плотно числовую ось [math]\displaystyle{ \left( -\infty, +\infty \right) }[/math].

Базис Шаудера

Система векторов [math]\displaystyle{ \{e_n\} }[/math] топологического векторного пространства [math]\displaystyle{ L }[/math] называется базисом Шаудера (в честь Шаудера), если каждый элемент [math]\displaystyle{ f \in L }[/math] разлагается в единственный, сходящийся к [math]\displaystyle{ f }[/math] ряд по [math]\displaystyle{ \{e_n\} }[/math]:

[math]\displaystyle{ f= \sum_{i=1}^{\infty} f_i e_i , }[/math]

где [math]\displaystyle{ f_i }[/math] — числа, называемые коэффициентами разложения вектора [math]\displaystyle{ f }[/math] по базису [math]\displaystyle{ \{e_n\} }[/math].

Чтобы подчеркнуть отличие определения базиса Гамеля для общих линейных пространств (допускаются только конечные суммы) от базиса Шаудера для топологических векторных пространств (допускается разложение в сходящийся ряд), для первого часто используют термин линейный базис, оставляя термин базис для разложений в ряды. Мощность линейного базиса называют также линейной размерностью. В конечномерных пространствах эти определения совпадают из-за конечности базиса. В бесконечномерных пространствах эти определения существенно различаются и линейная размерность может быть строго больше мощности базиса Шаудера.

Например, никакое бесконечномерное Гильбертово пространство не имеет счетного линейного базиса, хотя может иметь счетные базисы Шаудера с разложением в ряд, в том числе, ортонормированные базисы. Все ортонормированные базисы гильбертовых пространств являются базисами Шаудера, например, множество функций [math]\displaystyle{ \{1,\frac{1}{\sqrt{2}}\sin(2\pi nx), \frac{1}{\sqrt{2}} \cos(2\pi nx)\mid n=1,2,\dots\} }[/math] является базисом Шаудера в пространстве [math]\displaystyle{ L^2[0,1] }[/math]. В более общих банаховых пространствах понятие ортонормированного базиса неприменимо, но часто удаётся построить базисы Шаудера, не использующие ортогональности.

Пример: базис Шаудера для пространства непрерывных функций C[a, b]

[math]\displaystyle{ C[a,b] }[/math] — банахово пространство с нормой [math]\displaystyle{ \|f\| = \max_{x \in [a,b]}|f(x)| }[/math]. Для разложений в ряды Фурье и обобщенные ряды Фурье по ортонормированным системам функций легко доказывается сходимость в гильбертовом пространстве [math]\displaystyle{ L^2[a,b] }[/math], но не в [math]\displaystyle{ C[a,b] }[/math]. Шаудер сконструировал базис Шаудера [math]\displaystyle{ \{e_n\} }[/math] для [math]\displaystyle{ C[a,b] }[/math]. Пусть [math]\displaystyle{ \{x_0, x_1,\dots,x_n,\dots\} }[/math] — плотное счетное множество точек на [math]\displaystyle{ [a,b] }[/math], [math]\displaystyle{ x_0=a }[/math], [math]\displaystyle{ x_1=b }[/math], остальные точки могут быть, например, всеми рациональными точками отрезка [math]\displaystyle{ [a,b] }[/math], упорядоченными произвольным образом. Положим: [math]\displaystyle{ e_0=1 }[/math], [math]\displaystyle{ e_1=(x-a)/(b-a) }[/math] — линейная функция. Определим кусочно-линейную функцию [math]\displaystyle{ e_n(x) }[/math] так, чтобы [math]\displaystyle{ e_n(x_i)=0 }[/math] при [math]\displaystyle{ i=0,1,\dots,n-1 }[/math] и [math]\displaystyle{ e_n(x_n)=1 }[/math]. Точки [math]\displaystyle{ x_0, x_1, x_2,\dots,x_{n-1} }[/math] разбивают [math]\displaystyle{ [a,b] }[/math] на [math]\displaystyle{ n-1 }[/math] отрезок. Точка [math]\displaystyle{ x_n }[/math] лежит строго внутри одного из них. Пусть это [math]\displaystyle{ I_n=[x_j,x_k] }[/math] для каких-то [math]\displaystyle{ j, k \in \{0,\dots,n-1\} }[/math] (порядок нумерации чисел [math]\displaystyle{ x_0, x_1, x_2,\dots }[/math] не соответствует их величине).

Разложение непрерывной функции по базису Шаудера. Показано построение [math]\displaystyle{ L_{5}(x) }[/math]. Красным цветом на графике выделен участок, на котором [math]\displaystyle{ L_{5} }[/math] отличается от [math]\displaystyle{ L_{4} }[/math] (синяя ломаная).

Положим:

[math]\displaystyle{ e_n(x)=0 }[/math] вне отрезка [math]\displaystyle{ I_n=[x_j,x_k], }[/math]

[math]\displaystyle{ e_n(x)=\frac{x-x_j}{x_n-x_j} }[/math] при [math]\displaystyle{ x \in [x_j,x_n], }[/math]

[math]\displaystyle{ e_n(x)=\frac{x_k-x}{x_k-x_n} }[/math] при [math]\displaystyle{ x \in [x_n,x_k]. }[/math]

Полученная система кусочно-линейных «шапочек» и есть искомый базис Шаудера. Коэффициенты разложения произвольной функции [math]\displaystyle{ f(x) \in C[a,b] }[/math] по этому базису выражаются по явным рекуррентным формулам через последовательность значений [math]\displaystyle{ f(x_i) }[/math]. Частичная сумма первых [math]\displaystyle{ n+1 }[/math] членов ряда

[math]\displaystyle{ L_n(x)= \sum_{i=0}^{n} f_i e_i(x) , }[/math]

является в данном случае кусочно-линейной аппроксимацией [math]\displaystyle{ f(x) }[/math] с узлами в точках [math]\displaystyle{ x_0, x_1, x_2,\dots,x_{n} }[/math]; формула для коэффициентов [math]\displaystyle{ f_n =f(x_n)-L_{n-1}(x_n); \; \; f_0=f(a) }[/math] (см. Рис.)

Проблема базиса

Базисы Шаудера построены для большинства известных примеров банаховых пространств, однако проблема Банаха — Шаудера о существовании базиса Шаудера в каждом сепарабельном банаховом пространстве не поддавалась решению более 50 лет и лишь в 1972 году была решена отрицательно: существуют сепарабельные банаховы пространства без базиса Шаудера (контрпримеры Энфло, Шанковского, Дэви и Фигеля).

Применение в кристаллографии

В векторной алгебре с помощью векторного произведения и смешанного произведения определяется понятие взаимного базиса к базису в трёхмерном евклидовом пространстве и используется для доказательства некоторых утверждений, связанных со смешанным произведением и углами между векторами. В кристаллографии взаимный базис называется кристаллографическим определением базиса, на основе которого определяется обратная решётка.

См. также

• Репер — близкое понятие.
• Ортогональный базис — специальный класс базисов (базисов Шаудера) для пространств со скалярным произведением (Гильбертово пространство).
• Базис Грёбнера
• Базис Рисса
• Конечномерное пространство
• Флаг (математика)

Литература

• Кутателадзе С. С., Основы функционального анализа. — 4 изд., испр. — Новосибирск: Изд-во Ин-та Математики СО РАН, 2001. — XII+354 c.