Непрерывная функция

Эта статья — о непрерывной числовой функции. О непрерывных отображениях в различных разделах математики см. непрерывное отображение.

Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения. Вариацию этого понятия для функций комплексной переменной см. в статье Комплексный анализ.

Определение

Пусть [math]\displaystyle{ D\subset\R }[/math] и [math]\displaystyle{ f: D\to\R }[/math]. Существует несколько эквивалентных определений непрерывности функции в точке [math]\displaystyle{ x_0\in D }[/math].

• Определение через предел: функция [math]\displaystyle{ f }[/math] непрерывна в точке [math]\displaystyle{ x_0 }[/math], предельной для множества [math]\displaystyle{ D }[/math], если [math]\displaystyle{ f }[/math] имеет предел в точке [math]\displaystyle{ x_0 }[/math], и этот предел совпадает со значением функции [math]\displaystyle{ f(x_0) }[/math]:

  [math]\displaystyle{ \lim_{x\to x_0} f(x) = f(x_0) }[/math]

• Определение, использующее ε-δ-формализм: функция [math]\displaystyle{ f }[/math] непрерывна в точке [math]\displaystyle{ x_0\in D }[/math], если для любого [math]\displaystyle{ \varepsilon\gt 0 }[/math] существует [math]\displaystyle{ \delta\gt 0 }[/math] такое, что для любого [math]\displaystyle{ x\in D }[/math],

  [math]\displaystyle{ |x-x_0|\lt \delta \Rightarrow |f(x)-f(x_0)|\lt \varepsilon. }[/math]

Комментарий: По сравнению с определением предела функции по Коши в определении непрерывности нет требования, обязывающего все значения аргумента [math]\displaystyle{ x }[/math] удовлетворять условию [math]\displaystyle{ 0 \lt \left\vert x - a \right\vert }[/math], то есть быть отличными от а.

• Определение, использующее o-символику: функция [math]\displaystyle{ f }[/math] непрерывна в точке [math]\displaystyle{ x_0 }[/math], если

  [math]\displaystyle{ f(x_0+\delta) = f(x_0) + o(1) }[/math], при [math]\displaystyle{ \delta \to 0 }[/math].

• Определение через колебания: функция непрерывна в точке, если её колебание в данной точке равно нулю.

Функция [math]\displaystyle{ f }[/math] непрерывна на множестве [math]\displaystyle{ E }[/math], если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция [math]\displaystyle{ f }[/math] класса [math]\displaystyle{ C^0 }[/math] и пишут: [math]\displaystyle{ f\in C^0(E) }[/math] или, подробнее, [math]\displaystyle{ f\in C^0(E, \mathbb{R}) }[/math].

Точки разрыва

Запрос «Точка разрыва» перенаправляется сюда; см. также другие значения.

Если условие, входящее в определение непрерывности функции, в некоторой точке нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если [math]\displaystyle{ A }[/math] — значение функции [math]\displaystyle{ f }[/math] в точке [math]\displaystyle{ a }[/math], то предел такой функции (если он существует) не совпадает с [math]\displaystyle{ A }[/math]. На языке окрестностей условие разрывности функции [math]\displaystyle{ f }[/math] в точке [math]\displaystyle{ a }[/math] получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки [math]\displaystyle{ A }[/math] области значений функции [math]\displaystyle{ f }[/math], что как бы мы близко не подходили к точке [math]\displaystyle{ a }[/math] области определения функции [math]\displaystyle{ f }[/math], всегда найдутся такие точки, чьи образы будут за пределами окрестности точки [math]\displaystyle{ A }[/math].

Классификация точек разрыва в R¹

Классификация разрывов функций [math]\displaystyle{ f: X \to Y }[/math] зависит от того, как устроены множества X и Y. Здесь приведена классификация для простейшего случая — [math]\displaystyle{ f: \mathbb{R} \to \mathbb{R} }[/math]. Таким же образом классифицируют и особые точки (точки, где функция не определена). Стоит заметить, что классификация в [math]\displaystyle{ \mathbb{R} }[/math] различается от автора к автору.

Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:

• если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. К точкам разрыва первого рода относят устранимые разрывы и скачки.
• если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. К точкам разрыва второго рода относят полюса и точки существенного разрыва.

• 

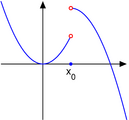
  Устранимый разрыв

• 

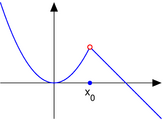
  Разрыв типа «скачок»

• 

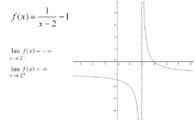
  Особая точка типа «полюс». Если доопределить функцию для x=2 — получится разрыв «полюс».

• 

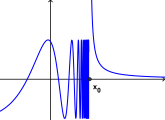
  Точка существенного разрыва

Устранимая точка разрыва

Если предел функции существует и конечен, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:

[math]\displaystyle{ \lim\limits_{x\to a} f(x) \neq f(a) }[/math],

то точка [math]\displaystyle{ a }[/math] называется точкой устранимого разрыва функции [math]\displaystyle{ f }[/math] (в комплексном анализе — устранимая особая точка).

Если «поправить» функцию [math]\displaystyle{ f }[/math] в точке устранимого разрыва и положить [math]\displaystyle{ f(a) = \lim\limits_{x\to a} f(x) }[/math], то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.

Точка разрыва «скачок»

Разрыв «скачок» возникает, если

[math]\displaystyle{ \lim\limits_{x\to a-0} f(x) \neq \lim\limits_{x\to a+0} f(x) }[/math].

Точка разрыва «полюс»

Разрыв «полюс» возникает, если один из односторонних пределов бесконечен.

[math]\displaystyle{ \lim\limits_{x\to a-0} f(x) = \pm \infty }[/math] или [math]\displaystyle{ \lim\limits_{x\to a+0} f(x) = \pm \infty }[/math].

Точка существенного разрыва

В точке существенного разрыва хотя бы один из односторонних пределов вообще отсутствует.

Классификация изолированных особых точек в Rⁿ, n>1

Для функций [math]\displaystyle{ f: \mathbb{R}^n \to \mathbb{R}^n }[/math] и [math]\displaystyle{ f: \mathbb{C} \to \mathbb{C} }[/math] нет нужды работать с точками разрыва, зато часто приходится работать с особыми точками (точками, где функция не определена). Классификация изолированных особых точек (то есть таких, где в какой-то окрестности нет других особых точек) сходная.

• Если [math]\displaystyle{ \exists \lim\limits_{x\to a} f(x) }[/math], то это устранимая особая точка (аналогично функции действительного аргумента).
• Полюс определяется как [math]\displaystyle{ \lim\limits_{x\to a} f(x) = \infty }[/math]. В многомерных пространствах, если модуль числа растёт, считается, что [math]\displaystyle{ f(x) \to \infty }[/math], каким путём бы он ни рос.
• Если предел вообще не существует, это существенная особая точка.

Понятие «скачок» отсутствует. То, что в [math]\displaystyle{ \mathbb{R} }[/math] считается скачком, в пространствах бóльших размерностей — существенная особая точка.

Свойства

Локальные

• Функция, непрерывная в точке [math]\displaystyle{ a }[/math], является ограниченной в некоторой окрестности этой точки.
• Если функция [math]\displaystyle{ f }[/math] непрерывна в точке [math]\displaystyle{ a }[/math] и [math]\displaystyle{ f(a)\gt 0 }[/math] (или [math]\displaystyle{ f(a)\lt 0 }[/math]), то [math]\displaystyle{ f(x)\gt 0 }[/math] (или [math]\displaystyle{ f(x)\lt 0 }[/math]) для всех [math]\displaystyle{ x }[/math], достаточно близких к [math]\displaystyle{ a }[/math].
• Если функции [math]\displaystyle{ f }[/math] и [math]\displaystyle{ g }[/math] непрерывны в точке [math]\displaystyle{ a }[/math], то функции [math]\displaystyle{ f+g }[/math] и [math]\displaystyle{ f \cdot g }[/math] тоже непрерывны в точке [math]\displaystyle{ a }[/math].
• Если функции [math]\displaystyle{ f }[/math] и [math]\displaystyle{ g }[/math] непрерывны в точке [math]\displaystyle{ a }[/math] и при этом [math]\displaystyle{ g(a)\neq 0 }[/math], то функция [math]\displaystyle{ f/g }[/math] тоже непрерывна в точке [math]\displaystyle{ a }[/math].
• Если функция [math]\displaystyle{ f }[/math] непрерывна в точке [math]\displaystyle{ a }[/math] и функция [math]\displaystyle{ g }[/math] непрерывна в точке [math]\displaystyle{ b=f(a) }[/math], то их композиция [math]\displaystyle{ h=g\circ f }[/math] непрерывна в точке [math]\displaystyle{ a }[/math].

Глобальные

• Теорема о равномерной непрерывности: функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
• Теорема Вейерштрасса о функции на компакте: функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
• Областью значений функции [math]\displaystyle{ f }[/math], непрерывной на отрезке [math]\displaystyle{ [a,b] }[/math], является отрезок [math]\displaystyle{ [\min f, \ \max f], }[/math] где минимум и максимум берутся по отрезку [math]\displaystyle{ [a,b] }[/math].
• Если функция [math]\displaystyle{ f }[/math] непрерывна на отрезке [math]\displaystyle{ [a,b] }[/math] и [math]\displaystyle{ f(a)\cdot f(b)\lt 0, }[/math] то существует точка [math]\displaystyle{ \xi \in (a,b), }[/math] в которой [math]\displaystyle{ f(\xi)=0 }[/math].
• Теорема о промежуточном значении: если функция [math]\displaystyle{ f }[/math] непрерывна на отрезке [math]\displaystyle{ [a,b] }[/math] и число [math]\displaystyle{ \varphi }[/math] удовлетворяет неравенству [math]\displaystyle{ f(a)\lt \varphi \lt f(b) }[/math] или неравенству [math]\displaystyle{ f(a)\gt \varphi \gt f(b), }[/math] то существует точка [math]\displaystyle{ \xi \in (a,b), }[/math] в которой [math]\displaystyle{ f(\xi)=\varphi }[/math].
• Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
• Монотонная функция на отрезке [math]\displaystyle{ [a,b] }[/math] непрерывна в том и только в том случае, когда область её значений является отрезком с концами [math]\displaystyle{ f(a) }[/math] и [math]\displaystyle{ f(b) }[/math].
• Если функции [math]\displaystyle{ f }[/math] и [math]\displaystyle{ g }[/math] непрерывны на отрезке [math]\displaystyle{ [a,b] }[/math], причем [math]\displaystyle{ f(a)\lt g(a) }[/math] и [math]\displaystyle{ f(b) \gt g(b), }[/math] то существует точка [math]\displaystyle{ \xi \in (a,b), }[/math] в которой [math]\displaystyle{ f(\xi)=g(\xi). }[/math] Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.

Примеры

Элементарные функции

Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.

Функция с устранимым разрывом

Функция [math]\displaystyle{ f\colon\mathbb{R} \to \mathbb{R}, }[/math] задаваемая формулой

[math]\displaystyle{ f(x) = \begin{cases} \frac{\sin x}{x}, & x \neq 0 \\ 0, & x = 0 \end{cases} }[/math]

непрерывна в любой точке [math]\displaystyle{ x \neq 0. }[/math] Точка [math]\displaystyle{ x=0 }[/math] является точкой устранимого разрыва, ибо предел функции

[math]\displaystyle{ \lim\limits_{x \to 0} f(x) = \lim\limits_{x \to 0} \frac{\sin x}{x} = 1 \neq f(0). }[/math]

Функция знака

Функция

[math]\displaystyle{ f(x) = \sgn x = \begin{cases} -1, & x \lt 0 \\ 0, & x = 0 \\ 1, & x \gt 0 \end{cases},\quad x\in \R }[/math]

называется функцией знака.

Эта функция непрерывна в каждой точке [math]\displaystyle{ x \neq 0 }[/math].

Точка [math]\displaystyle{ x=0 }[/math] является точкой разрыва первого рода, причём

[math]\displaystyle{ \lim\limits_{x \to 0-}f(x) = -1 \neq 1 = \lim\limits_{x \to 0+}f(x) }[/math],

в то время как в самой точке функция обращается в нуль.

Функция Хевисайда

Функция Хевисайда, определяемая как

[math]\displaystyle{ f(x) = \begin{cases} 1,& x \geqslant 0\\ 0, & x \lt 0 \end{cases},\quad x\in \mathbb{R} }[/math]

является всюду непрерывной, кроме точки [math]\displaystyle{ x=0 }[/math], где функция терпит разрыв первого рода. Тем не менее, в точке [math]\displaystyle{ x=0 }[/math] существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.

Аналогично, ступенчатая функция, определяемая как

[math]\displaystyle{ f(x) = \begin{cases} 1,& x \gt 0\\ 0, & x \leqslant 0 \end{cases},\quad x\in \mathbb{R} }[/math]

является примером непрерывной слева функции на всей области определения.

Функция Дирихле

Основная статья: Функция Дирихле

Функция

[math]\displaystyle{ f(x) = \begin{cases} 1,& x \in \mathbb{Q}\\ 0, & x \in \mathbb{R}\setminus\mathbb{Q} \end{cases} }[/math]

называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция разрывна в каждой точке, поскольку в сколь угодно малой окрестности любой точки имеются как рациональные, так и иррациональные числа.

Функция Римана

Основная статья: Функция Римана (ТФДП)

Функция

[math]\displaystyle{ f(x) = \begin{cases} \frac{1}{n},& x=\frac{m}{n}\in \mathbb{Q},\ \text{НОД}(m,n) = 1 \\ 0, & x \in \mathbb{R}\setminus\mathbb{Q} \end{cases} }[/math]

называется функцией Римана или «функцией Тома».

Эта функция непрерывна на множестве иррациональных чисел ([math]\displaystyle{ \mathbb{R}\setminus\mathbb{Q} }[/math]), поскольку предел функции в каждой иррациональной точке равен нулю (если последовательность [math]\displaystyle{ x_k = m_k/n_k \to x \notin \mathbb{Q} }[/math], то с необходимостью [math]\displaystyle{ n_k \to \infty }[/math]). Во всех же рациональных точках она разрывна.

Вариации и обобщения

Равномерная непрерывность

Основная статья: Равномерная непрерывность

Функция [math]\displaystyle{ f }[/math] называется равномерно непрерывной на [math]\displaystyle{ E }[/math], если для любого [math]\displaystyle{ \varepsilon\gt 0 }[/math] существует [math]\displaystyle{ \delta\gt 0 }[/math] такое, что для любых двух точек [math]\displaystyle{ x_1 }[/math] и [math]\displaystyle{ x_2 }[/math] таких, что [math]\displaystyle{ |x_1-x_2|\lt \delta }[/math], выполняется [math]\displaystyle{ |f(x_1)-f(x_2)|\lt \varepsilon }[/math].

Каждая равномерно непрерывная на множестве [math]\displaystyle{ E }[/math] функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.

Полунепрерывность

Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:

• функция [math]\displaystyle{ f }[/math] называется полунепрерывной снизу в точке [math]\displaystyle{ a }[/math], если для любого [math]\displaystyle{ \varepsilon\gt 0 }[/math] существует такая окрестность [math]\displaystyle{ U_E(a) }[/math], что [math]\displaystyle{ f(x)\gt f(a)-\varepsilon }[/math] для всякого [math]\displaystyle{ x\in U_E(a) }[/math];
• функция [math]\displaystyle{ f }[/math] называется полунепрерывной сверху в точке [math]\displaystyle{ a }[/math], если для любого [math]\displaystyle{ \varepsilon\gt 0 }[/math] существует такая окрестность [math]\displaystyle{ U_E(a) }[/math], что [math]\displaystyle{ f(x)\lt f(a)+\varepsilon }[/math] для всякого [math]\displaystyle{ x\in U_E(a) }[/math].

Между непрерывностью и полунепрерывностью имеется следующая связь:

• если взять функцию [math]\displaystyle{ f }[/math], непрерывную в точке [math]\displaystyle{ a }[/math], и уменьшить значение [math]\displaystyle{ f(a) }[/math] (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке [math]\displaystyle{ a }[/math];
• если взять функцию [math]\displaystyle{ f }[/math], непрерывную в точке [math]\displaystyle{ a }[/math], и увеличить значение [math]\displaystyle{ f(a) }[/math] (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке [math]\displaystyle{ a }[/math].

В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:

• если [math]\displaystyle{ f(a)=-\infty }[/math], то будем считать такую функцию полунепрерывной снизу в точке [math]\displaystyle{ a }[/math];
• если [math]\displaystyle{ f(a)=+\infty }[/math], то будем считать такую функцию полунепрерывной сверху в точке [math]\displaystyle{ a }[/math].

Односторонняя непрерывность

Функция [math]\displaystyle{ f }[/math] называется непрерывной слева (справа) в точке [math]\displaystyle{ x_0 }[/math] её области определения, если для одностороннего предела выполняется равенство: [math]\displaystyle{ f(x_0)=\lim\limits_{x\to x_0-} f(x) }[/math] [math]\displaystyle{ (f(x_0)=\lim\limits_{x\to x_0+} f(x)). }[/math]

Непрерывность почти всюду

На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция [math]\displaystyle{ f }[/math] такова, что она непрерывна всюду на [math]\displaystyle{ E }[/math], кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.

В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).

Литература

• Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.