Монотонная функция

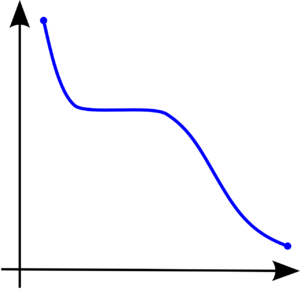

Моното́нная фу́нкция — функция одной переменной, определённая на некотором подмножестве действительных чисел, которая либо везде (на области своего определения) не убывает, либо везде не возрастает. Более точно, это функция [math]\displaystyle{ f }[/math], приращение которой [math]\displaystyle{ \Delta f = f(x')-f(x) }[/math] при [math]\displaystyle{ \Delta x = (x'- x) \gt 0 }[/math] не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное[1]. Если в дополнение приращение [math]\displaystyle{ \Delta f }[/math] не равно нулю, то функция называется стро́го моното́нной.
Функция называется возраста́ющей, если большему значению аргумента соответствует не меньшее (по другой терминологии — большее) значение функции. Функция называется убыва́ющей, если большему значению аргумента соответствует не большее (по другой терминологии — меньшее) значение функции.
Определения
Пусть дана функция [math]\displaystyle{ f:M \subset \R \to \R. }[/math] Тогда
- функция [math]\displaystyle{ f }[/math] называется возраста́ющей на [math]\displaystyle{ M }[/math], если
- [math]\displaystyle{ \forall x,y\in M,\; x \gt y \Rightarrow f(x) \ge f(y) }[/math].
- функция [math]\displaystyle{ f }[/math] называется стро́го возраста́ющей на [math]\displaystyle{ M }[/math], если
- [math]\displaystyle{ \forall x,y\in M,\; x \gt y \Rightarrow f(x) \gt f(y) }[/math].
- функция [math]\displaystyle{ f }[/math] называется убыва́ющей на [math]\displaystyle{ M }[/math], если
- [math]\displaystyle{ \forall x,y\in M,\; x \gt y \Rightarrow f(x) \le f(y) }[/math].
- функция [math]\displaystyle{ f }[/math] называется стро́го убыва́ющей на [math]\displaystyle{ M }[/math], если
- [math]\displaystyle{ \forall x,y\in M,\; x \gt y \Rightarrow f(x) \lt f(y) }[/math].
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Другая терминология
Иногда под терминами возрастающая (убывающая) функция подразумевается строго возрастающая (убывающая) функция. Тогда про нестрого возрастающую (убывающую) функцию говорят, неубывающая (невозрастающая)[2]:
- Функция [math]\displaystyle{ f(x) }[/math] называется возрастающей на некотором интервале, если для любых двух точек [math]\displaystyle{ x_1 }[/math] и [math]\displaystyle{ x_2 }[/math] этого интервала, таких что [math]\displaystyle{ x_1\lt x_2 }[/math], справедливо [math]\displaystyle{ f(x_1)\lt f(x_2) }[/math]. Другими словами, большему значению аргумента соответствует большее значение функции.
- Функция [math]\displaystyle{ f(x) }[/math] называется убывающей на некотором интервале, если для любых двух точек [math]\displaystyle{ x_1 }[/math] и [math]\displaystyle{ x_2 }[/math] этого интервала, таких что [math]\displaystyle{ x_1\lt x_2 }[/math], справедливо [math]\displaystyle{ f(x_1)\gt f(x_2) }[/math]. Другими словами, большему значению аргумента соответствует меньшее значение функции.
- Функция [math]\displaystyle{ f(x) }[/math] называется неубывающей на некотором интервале, если для любых двух точек [math]\displaystyle{ x_1 }[/math] и [math]\displaystyle{ x_2 }[/math] этого интервала, таких что [math]\displaystyle{ x_1\lt x_2 }[/math], справедливо [math]\displaystyle{ f(x_1) \le f(x_2) }[/math].
- Функция [math]\displaystyle{ f(x) }[/math] называется невозрастающей на некотором интервале, если для любых двух точек [math]\displaystyle{ x_1 }[/math] и [math]\displaystyle{ x_2 }[/math] этого интервала, таких что [math]\displaystyle{ x_1\lt x_2 }[/math], справедливо [math]\displaystyle{ f(x_1) \ge f(x_2) }[/math].
- Возрастающие и убывающие функции называются строго монотонными, неубывающие и невозрастающие функции — монотонными.
Свойства монотонных функций
- Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
- Монотонная функция, [math]\displaystyle{ f:[a,b] \to \R, }[/math] определённая на замкнутом интервале, ограничена. В частности, она интегрируема по Лебегу.
- Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
- Монотонная функция [math]\displaystyle{ f:(a,b) \to \R }[/math] дифференцируема почти всюду относительно меры Лебега.
Условия монотонности функции
- (Критерий монотонности функции, имеющей производную на интервале) Пусть функция [math]\displaystyle{ f \in C \bigl( (a,b) \bigr) }[/math] непрерывна на [math]\displaystyle{ (a,b), }[/math] и имеет в каждой точке [math]\displaystyle{ x\in (a,b) }[/math] производную [math]\displaystyle{ f'(x). }[/math] Тогда
- [math]\displaystyle{ f }[/math] не убывает на [math]\displaystyle{ (a,b) }[/math] тогда и только тогда, когда [math]\displaystyle{ \forall x \in (a,b)\; f'(x) \ge 0; }[/math]
- [math]\displaystyle{ f }[/math] не возрастает на [math]\displaystyle{ (a,b) }[/math] тогда и только тогда, когда [math]\displaystyle{ \forall x \in (a,b)\; f'(x) \le 0. }[/math]
- (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция [math]\displaystyle{ f \in C \bigl( (a,b) \bigr) }[/math] непрерывна на [math]\displaystyle{ (a,b), }[/math] и имеет в каждой точке [math]\displaystyle{ x\in (a,b) }[/math] производную [math]\displaystyle{ f'(x). }[/math] Тогда
- если [math]\displaystyle{ \forall x \in (a,b)\; f'(x) \gt 0, }[/math] то [math]\displaystyle{ f }[/math] строго возрастает на [math]\displaystyle{ (a,b); }[/math]
- если [math]\displaystyle{ \forall x \in (a,b)\; f'(x) \lt 0, }[/math] то [math]\displaystyle{ f }[/math] строго убывает на [math]\displaystyle{ (a,b). }[/math]
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале [math]\displaystyle{ (a,b). }[/math] Точнее имеет место
- (Критерий строгой монотонности функции, имеющей производную на интервале) Пусть [math]\displaystyle{ f\in C\bigl( (a,b) \bigr), }[/math] и всюду на интервале определена производная [math]\displaystyle{ f'(x). }[/math] Тогда [math]\displaystyle{ f }[/math] строго возрастает на интервале [math]\displaystyle{ (a,b) }[/math] тогда и только тогда, когда выполнены следующие два условия:
- [math]\displaystyle{ \forall x \in (a,b) \; f'(x) \ge 0; }[/math]
- [math]\displaystyle{ \forall (c,d) \subset (a,b)\; \exists x\in (c,d)\; f'(x) \gt 0. }[/math]
Аналогично, [math]\displaystyle{ f }[/math] строго убывает на интервале [math]\displaystyle{ (a,b) }[/math] тогда и только тогда, когда выполнены следующие два условия:
- [math]\displaystyle{ \forall x \in (a,b) \; f'(x) \le 0; }[/math]
- [math]\displaystyle{ \forall (c,d) \subset (a,b)\; \exists x\in (c,d)\; f'(x) \lt 0. }[/math]
Примеры
- Функция [math]\displaystyle{ f(x)=x^3 }[/math] строго возрастает на всей числовой прямой, несмотря на то, что точка [math]\displaystyle{ x=0 }[/math] является стационарной, т.е. в этой точке [math]\displaystyle{ f'(x)=0 }[/math].
- Функция [math]\displaystyle{ f(x)= \sin x }[/math] является строго возрастающей не только на открытом интервале [math]\displaystyle{ (- \pi /2; \pi /2) }[/math], но и на замкнутом интервале [math]\displaystyle{ [- \pi /2; \pi /2] }[/math].
- Экспонента [math]\displaystyle{ f(x) = e^x }[/math] строго возрастает на всей числовой прямой.
- Константа [math]\displaystyle{ f(x) \equiv a,\; a\in \mathbb{R} }[/math] одновременно не возрастает и не убывает на всей числовой прямой.
- Канторова лестница — пример непрерывной монотонной функции, которая не является константой, но при этом имеет производную равную нулю в почти всех точках.
- Функция Минковского — пример сингулярной строго возрастающей функции.
Вариации и обобщения
- Отображение [math]\displaystyle{ f\colon X\to Y }[/math] между топологическими пространствами называется монотонным если каждая точка [math]\displaystyle{ y\in Y }[/math] имеет связный прообраз [math]\displaystyle{ f^{-1}(y) }[/math].[3]
Примечания
- ↑ Монотонная функция / Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 4. Непрерывность функции // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 146. — 672 с. — ISBN 5-482-00445-7.
- ↑ Collins, P. J. (1971). Concordant mappings and the concordant-dissonant factorization of an arbitrary continuous function. Proceedings of the American Mathematical Society, 27(3), 587-591.