Смешанное произведение
Сме́шанное произведе́ние [math]\displaystyle{ (\mathbf{a}, \mathbf{b}, \mathbf{c}) }[/math] векторов [math]\displaystyle{ \mathbf{a}, \mathbf{b}, \mathbf{c} }[/math] — скалярное произведение вектора [math]\displaystyle{ \mathbf{a} }[/math] на векторное произведение векторов [math]\displaystyle{ \mathbf{b} }[/math] и [math]\displaystyle{ \mathbf{c} }[/math]:
- [math]\displaystyle{ (\mathbf{a}, \mathbf{b}, \mathbf c) = \mathbf{a}\cdot\left(\mathbf{b}\times\mathbf c\right) }[/math].
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами [math]\displaystyle{ \mathbf a, \mathbf b, \mathbf c }[/math].
Свойства
- Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
- [math]\displaystyle{ (\mathbf a,\mathbf b,\mathbf c)=(\mathbf b,\mathbf c,\mathbf a)=(\mathbf c,\mathbf a,\mathbf b)=-(\mathbf b,\mathbf a,\mathbf c)=-(\mathbf c,\mathbf b,\mathbf a)=-(\mathbf a,\mathbf c,\mathbf b); }[/math]
- т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
- [math]\displaystyle{ \lang \mathbf a, [\mathbf b, \mathbf c]\rang = \lang [\mathbf a, \mathbf b], \mathbf c\rang }[/math]
- Смешанное произведение [math]\displaystyle{ ( \mathbf{a}, \mathbf{b}, \mathbf{c} ) }[/math] в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов [math]\displaystyle{ \mathbf{a}, \mathbf{b} }[/math] и [math]\displaystyle{ \mathbf{c} }[/math]:
- [math]\displaystyle{ ( \mathbf{a}, \mathbf{b}, \mathbf{c} ) = \begin{vmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \end{vmatrix}. }[/math]
- Смешанное произведение [math]\displaystyle{ ( \mathbf{a}, \mathbf{b}, \mathbf{c} ) }[/math] в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов [math]\displaystyle{ \mathbf{a}, \mathbf{b} }[/math] и [math]\displaystyle{ \mathbf{c} }[/math], взятому со знаком «минус»:
- [math]\displaystyle{ ( \mathbf{a}, \mathbf{b}, \mathbf{c} ) = - \begin{vmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \end{vmatrix}. }[/math]
- В частности,
- Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю.
- Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
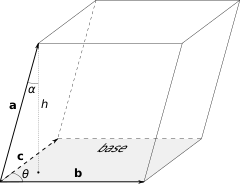
- Геометрический смысл — Смешанное произведение [math]\displaystyle{ ( \mathbf{a}, \mathbf{b}, \mathbf{c} ) }[/math] по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами [math]\displaystyle{ \mathbf{a}, \mathbf{b} }[/math] и [math]\displaystyle{ \mathbf{c} }[/math]; знак зависит от того, является ли эта тройка векторов правой или левой.
- Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими[1]:215.
- Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
- [math]\displaystyle{ (\mathbf a,\mathbf b,\mathbf c) = \sum_{i,j,k} \varepsilon_{ijk}a^i b^j c^k }[/math]
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
Обобщение
В [math]\displaystyle{ n }[/math]-мерном пространстве естественным обобщением смешанного произведения, имеющего смысл ориентированного объема, является определитель матрицы [math]\displaystyle{ n \times n }[/math], составленной из строк или столбцов, заполненных координатами векторов. Смысл этой величины — ориентированный [math]\displaystyle{ n }[/math]-мерный объем (подразумевается стандартный базис и тривиальная метрика).
В произвольном базисе произвольной размерности смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивиты соответствующей размерности:
- [math]\displaystyle{ (\mathbf a,\mathbf b,\mathbf c, \ldots) = \sum_{i,j,k,\ldots} \varepsilon_{ijk\ldots}a^i b^j c^k \ldots }[/math]
В двумерном пространстве таковым служит псевдоскалярное произведение.
См. также
- Двойное векторное произведение
- Векторное произведение
- Скалярное произведение
- Псевдоскалярное произведение
Примечания
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.