Векторное пространство

Ве́кторное простра́нство (лине́йное пространство) — математическая структура, представляющая собой набор элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр^[1]. Эти операции подчинены восьми аксиомам^[⇨]. Скаляры могут быть элементами вещественного, комплексного или любого другого поля чисел. Частным случаем подобного пространства является обычное трёхмерное евклидово пространство, векторы которого используются, к примеру, для представления физических сил. При этом вектор как элемент векторного пространства не обязательно должен быть задан в виде направленного отрезка. Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы^[2].

Векторные пространства являются предметом изучения линейной алгебры. Одна из главных характеристик векторного пространства — его размерность.^[⇨] Размерность представляет собой максимальное число линейно независимых элементов пространства, то есть, прибегая к грубой геометрической интерпретации, число направлений, которые невозможно выразить друг через друга посредством только операций сложения и умножения на скаляр. Векторное пространство можно наделить дополнительными структурами, например, нормой или скалярным произведением. Подобные пространства естественным образом появляются в математическом анализе, преимущественно в виде бесконечномерных функциональных пространств^[англ.], где в качестве векторов выступают функции. Многие проблемы анализа требуют выяснить, сходится ли последовательность векторов к данному вектору. Рассмотрение таких вопросов возможно в векторных пространствах с дополнительной структурой, в большинстве случаев — подходящей топологией, что позволяет определить понятия близости и непрерывности. Такие топологические векторные пространства, в частности, банаховы и гильбертовы, допускают более глубокое изучение.

Первые труды, предвосхитившие введение понятия векторного пространства, относятся к XVII веку. Именно тогда своё развитие получили аналитическая геометрия, учения о матрицах, системах линейных уравнений, евклидовых векторах.

Определение

Линейное, или векторное, пространство [math]\displaystyle{ V(F) }[/math] над полем [math]\displaystyle{ F }[/math] — это упорядоченная четвёрка [math]\displaystyle{ (V, F, +, \cdot) }[/math], где

[math]\displaystyle{ V }[/math] — непустое множество элементов произвольной природы, которые называются векторами.
[math]\displaystyle{ F }[/math] — поле, элементы которого называются скалярами.
Определена операция сложения векторов [math]\displaystyle{ V \times V \to V }[/math], сопоставляющая каждой паре элементов [math]\displaystyle{ \mathbf{x}, \mathbf{y} }[/math] множества [math]\displaystyle{ V }[/math] единственный элемент множества [math]\displaystyle{ V }[/math], называемый их суммой и обозначаемый [math]\displaystyle{ \mathbf{x} + \mathbf{y} }[/math].
Определена операция умножения векторов на скаляры [math]\displaystyle{ F \times V \to V }[/math], сопоставляющая каждому элементу [math]\displaystyle{ \lambda }[/math] поля [math]\displaystyle{ F }[/math] и каждому элементу [math]\displaystyle{ \mathbf{x} }[/math] множества [math]\displaystyle{ V }[/math] единственный элемент множества [math]\displaystyle{ V }[/math], обозначаемый [math]\displaystyle{ \lambda \cdot \mathbf{x} }[/math] или [math]\displaystyle{ \lambda \mathbf{x} }[/math].

Заданные операции должны удовлетворять следующим аксиомам — аксиомам линейного (векторного) пространства:

[math]\displaystyle{ \mathbf{x} + \mathbf{y} = \mathbf{y} + \mathbf{x} }[/math] для любых [math]\displaystyle{ \mathbf{x}, \mathbf{y} \in V }[/math] (коммутативность сложения);
[math]\displaystyle{ \mathbf{x} + (\mathbf{y} + \mathbf{z}) = (\mathbf{x} + \mathbf{y}) + \mathbf{z} }[/math] для любых [math]\displaystyle{ \mathbf{x}, \mathbf{y}, \mathbf{z} \in V }[/math] (ассоциативность сложения);
существует такой элемент [math]\displaystyle{ \mathbf{0} \in V }[/math], что [math]\displaystyle{ \mathbf{x} + \mathbf{0} = \mathbf{0} + \mathbf{x} = \mathbf{x} }[/math] для любого [math]\displaystyle{ \mathbf{x} \in V }[/math] (существование нейтрального элемента относительно сложения), называемый нулевым вектором, или просто нулём, пространства [math]\displaystyle{ V }[/math];
для любого [math]\displaystyle{ \mathbf{x} \in V }[/math] существует такой элемент [math]\displaystyle{ -\mathbf{x} \in V }[/math], что [math]\displaystyle{ \mathbf{x} + (-\mathbf{x}) = \mathbf{0} }[/math], называемый вектором, противоположным вектору [math]\displaystyle{ \mathbf{x} }[/math];
[math]\displaystyle{ \alpha(\beta\mathbf{x}) = (\alpha\beta)\mathbf{x} }[/math] (ассоциативность умножения на скаляр);
[math]\displaystyle{ 1 \cdot \mathbf{x} = \mathbf{x} }[/math] (унитарность: умножение на нейтральный (по умножению) элемент поля [math]\displaystyle{ F }[/math] сохраняет вектор).
[math]\displaystyle{ (\alpha + \beta)\mathbf{x} = \alpha \mathbf{x} + \beta \mathbf{x} }[/math] (дистрибутивность умножения вектора на скаляр относительно сложения скаляров);
[math]\displaystyle{ \alpha(\mathbf{x} + \mathbf{y}) = \alpha \mathbf{x} + \alpha \mathbf{y} }[/math] (дистрибутивность умножения вектора на скаляр относительно сложения векторов).

Таким образом, операция сложения задаёт на множестве [math]\displaystyle{ V }[/math] структуру (аддитивной) абелевой группы.

Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами (например, множество пар действительных чисел [math]\displaystyle{ \mathbb{R}^2 }[/math] может быть двумерным векторным пространством над полем действительных чисел либо одномерным — над полем комплексных чисел).

Простейшие свойства

Векторное пространство является абелевой группой по сложению.
Нейтральный элемент [math]\displaystyle{ \mathbf{0} \in V }[/math] является единственным, что вытекает из групповых свойств.
[math]\displaystyle{ 0\cdot\mathbf{x} = \mathbf{0} }[/math] для любого [math]\displaystyle{ \mathbf{x} \in V }[/math].
Для любого [math]\displaystyle{ \mathbf{x} \in V }[/math] противоположный элемент [math]\displaystyle{ -\mathbf{x} \in V }[/math] является единственным, что вытекает из групповых свойств.
[math]\displaystyle{ 1\cdot\mathbf{x} = \mathbf{x} }[/math] для любого [math]\displaystyle{ \mathbf{x} \in V }[/math].
[math]\displaystyle{ (-\alpha)\cdot\mathbf{x} = \alpha\cdot(-\mathbf{x}) = -(\alpha\mathbf{x}) }[/math] для любых [math]\displaystyle{ \alpha \in F }[/math] и [math]\displaystyle{ \mathbf{x} \in V }[/math].
[math]\displaystyle{ \alpha\cdot \mathbf{0} = \mathbf{0} }[/math] для любого [math]\displaystyle{ \alpha \in F }[/math].

Связанные определения и свойства

Линейная оболочка

Линейная оболочка (англ. Linear span) [math]\displaystyle{ \mathcal V(X) }[/math] подмножества [math]\displaystyle{ X }[/math] линейного пространства [math]\displaystyle{ V }[/math] — пересечение всех подпространств [math]\displaystyle{ V }[/math], содержащих [math]\displaystyle{ X }[/math].

Определение: Возьмем векторное пространство [math]\displaystyle{ (\mathcal{V}, \mathcal{F}) }[/math] и множество векторов [math]\displaystyle{ S := \{ \boldsymbol{x}_1, \boldsymbol{x}_2, \dots, \boldsymbol{x}_n \} \in \mathcal{V} }[/math]. Линейной оболочкой [math]\displaystyle{ S }[/math], то есть span(S), является множество всех векторов, являющихся линейной комбинацией векторов [math]\displaystyle{ S }[/math]:

[math]\displaystyle{ \text{Span}(S) := \left\{ \sum_{i=1}^n c_i\boldsymbol{x}_i \mid c_1, \dots, c_n \in \mathcal{F} \right\} }[/math]

Подпространство

Линейное подпространство это тоже, что и линейная оболочка без принятие во внимание конкретных векторов, являющихся базисом линейной оболочки.

Алгебраическое определение: Линейное подпространство, или векторное подпространство, ― непустое подмножество [math]\displaystyle{ K }[/math] линейного пространства [math]\displaystyle{ V }[/math] (или [math]\displaystyle{ R^n }[/math]) такое, что [math]\displaystyle{ K }[/math] само является линейным пространством по отношению к определённым в [math]\displaystyle{ V }[/math] (или [math]\displaystyle{ R^n }[/math]) действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как [math]\displaystyle{ \mathrm{Lat}(V) }[/math]. Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

оно было непустым: нулевой вектор также принадлежит [math]\displaystyle{ K }[/math].
оно было замкнуто относительно операции умножения на скаляр: для всякого вектора [math]\displaystyle{ \mathbf{x}\in K }[/math] вектор [math]\displaystyle{ \alpha\mathbf{x} }[/math] также принадлежал [math]\displaystyle{ K }[/math] при любом [math]\displaystyle{ \alpha\in F }[/math];
оно было замкнуто относительно операции сложения: для всяких векторов [math]\displaystyle{ \mathbf{x}, \mathbf{y} \in K }[/math] вектор [math]\displaystyle{ \mathbf{x}+\mathbf{y} }[/math] также принадлежал [math]\displaystyle{ K }[/math].

Примеры

Множество [math]\displaystyle{ R^n }[/math] является подпространством самого себя: оно содержит нуль и замкнуто относительно умножения на скаляр и сложения.
Множество [math]\displaystyle{ \{0\} }[/math], содержащее только нуль, является подпространством [math]\displaystyle{ R^n }[/math], посокольку, во-первых, содержит нуль - соответствие первому утверждению; во-вторых, умножение любого скаляра на нуль дает нуль, следовательно множество замкнуто относительно умножения на скаляр - соответствие второму утверждению; в-третьих, сложение нулей дает нуль, следовательно множество замкнуто относительно сложения - соответствие третьему утверждению.
Прямая, проходящая через начало координат, является подпространством, поскольку выполняются все три утверждения: включает в себя ноль, замкнуто относительно умножения на скаляр и сложения.

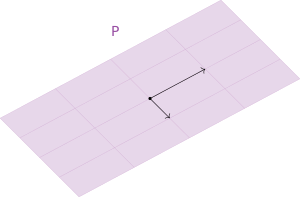
Плоскость, проходящая через начало координат, является подпространством.

Объединение прямой и пространства в [math]\displaystyle{ R³ }[/math] не является подпространством (См. рисунок). Оно содержат ноль и замкнуто относительно умножения на скаляр, но не замкнуто относительно сложения. Как видно на рисунке, вектор суммы (красным цветом) векторов на прямой (черным цветом) и на плоскости (черным цветом) не находится, ни на прямой, ни на плоскости. То есть условие замкнутости множества относительно сложения не выполнено.

Линейные комбинации

Формальное выражение вида

[math]\displaystyle{ \alpha_1\mathbf{x}_1 + \alpha_2\mathbf{x}_2 + \ldots + \alpha_n\mathbf{x}_n }[/math]

называется^[3] линейной комбинацией элементов [math]\displaystyle{ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n \in V }[/math] с коэффициентами [math]\displaystyle{ \alpha_1, \alpha_2, \ldots, \alpha_n \in F }[/math].

В действительности данное определение (и приводимые ниже) приложимо не только к комбинациям векторов, но и к комбинациям любых других объектов, для которых подобные суммы вообще имеют смысл (например, к комбинациям точек аффинного пространства).

Линейная комбинация называется:

нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.
барицентрической, если сумма её коэффициентов равна 1^[4],
выпуклой, если сумма её коэффициентов равна 1 и все коэффициенты неотрицательны,
сбалансированной, если сумма её коэффициентов равна 0.

Базис и размерность

Векторы [math]\displaystyle{ \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n }[/math] называются^[5] линейно зависимыми, если существует их нетривиальная линейная комбинация, значение которой равно нулю; то есть

[math]\displaystyle{ \alpha_1\mathbf{x}_1 + \alpha_2\mathbf{x}_2 + \ldots + \alpha_n\mathbf{x}_n = \mathbf{0} }[/math]

при некоторых ненулевых коэффициентах [math]\displaystyle{ \alpha_1, \alpha_2, \ldots, \alpha_n \in F }[/math] (то есть если хотя бы один из [math]\displaystyle{ \alpha_1, \alpha_2, \ldots, \alpha_n }[/math] не равен нулю).

В противном случае эти векторы называются линейно независимыми.

Данное определение допускает следующее обобщение: бесконечное множество векторов из [math]\displaystyle{ V }[/math] называется линейно зависимым, если линейно зависимо некоторое конечное его подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо.

Можно показать^[6], что число элементов (мощность) максимального линейно независимого множества элементов векторного пространства не зависит от выбора этого множества. Данное число называется рангом, или размерностью, пространства, а само это множество — базисом (базисом Га́меля, или линейным базисом). Элементы базиса именуют базисными векторами. Размерность пространства чаще всего обозначается символом [math]\displaystyle{ {\rm dim} }[/math].

Таким образом, размерность векторного пространства является либо неотрицательным целым числом (в частности, равным нулю, если пространство состоит из одного лишь нулевого вектора), либо бесконечностью (точнее, мощностью бесконечного множества). В первом случае векторное пространство называется конечномерным, а во втором — бесконечномерным (например, бесконечномерным является пространство непрерывных функций). Традиционно изучение конечномерных векторных пространств и их отображений относится к линейной алгебре, а изучение бесконечномерных векторных пространств — к функциональному анализу. Во втором случае существенную роль играет вопрос о разложимости данного элемента по заданной бесконечной системе функций, то есть о сходимости соответствующих бесконечных сумм, для чего бесконечномерное векторное пространство рассматривается вместе с дополнительной структурой, позволяющей определять сходимость, например, с метрикой или топологией.

Свойства базиса:

Любые [math]\displaystyle{ n }[/math] линейно независимых элементов [math]\displaystyle{ n }[/math]-мерного пространства образуют базис этого пространства.

Любой вектор [math]\displaystyle{ \mathbf{x} \in V }[/math] можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:
[math]\displaystyle{ \mathbf{x} = \alpha_1\mathbf{x}_1 + \alpha_2\mathbf{x}_2 + \ldots + \alpha_n\mathbf{x}_n }[/math].

Изоморфизм

Два линейных пространства [math]\displaystyle{ V'(F) }[/math] и [math]\displaystyle{ V''(F) }[/math] называются изоморфными, если между векторами [math]\displaystyle{ x' \in V' }[/math] и [math]\displaystyle{ x'' \in V'' }[/math] можно установить взаимно однозначное соответствие таким образом, что выполняются условия:

если вектору [math]\displaystyle{ \mathbf{x}' \in V' }[/math] соответствует вектор [math]\displaystyle{ \mathbf{x}'' \in V'' }[/math], а вектору [math]\displaystyle{ \mathbf{y}' \in V' }[/math] соответствует вектор [math]\displaystyle{ \mathbf{y}'' \in V'' }[/math], то вектору [math]\displaystyle{ \mathbf{x}' + \mathbf{y}' \in V' }[/math] соответствует вектор [math]\displaystyle{ \mathbf{x}'' + \mathbf{y}'' \in V'' }[/math]
если вектору [math]\displaystyle{ \mathbf{x}' \in V' }[/math] соответствует вектор [math]\displaystyle{ \mathbf{x}'' \in V'' }[/math], и [math]\displaystyle{ \lambda }[/math] - элемент поля [math]\displaystyle{ F }[/math], то вектору [math]\displaystyle{ \lambda \mathbf{x}' \in V' }[/math] соответствует вектор [math]\displaystyle{ \lambda \mathbf{x}'' \in V'' }[/math]^[7]

Примеры

Нулевое пространство, единственным элементом которого является ноль.
Пространство всех функций [math]\displaystyle{ X\to F }[/math] с конечным носителем образует векторное пространство размерности, равной мощности [math]\displaystyle{ X }[/math].
Поле действительных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.
Любое поле является одномерным пространством над собой.
Пространства матриц и тензоров образуют линейное пространство.

Дополнительные структуры

См. также

Примечания

↑ Не следует путать понятия «умножение на скаляр» и «скалярное произведение».
↑ Ильин, Позняк, 2010, с. 45.
↑ Кострикин, Манин, 1986, с. 8.
↑ Кострикин, Манин, 1986, с. 198.
↑ Кострикин, Манин, 1986, с. 16.
↑ Кострикин, Манин, 1986, с. 14.
↑ Шилов Г. Е. Введение в теорию линейных пространств. — М., Л., Гостехтеориздат, 1952. — с. 70

Литература

Гельфанд И. М. Лекции по линейной алгебре. — 5-е. — М.: Добросвет, МЦНМО, 1998. — 319 с. — ISBN 5-7913-0015-8.
Гельфанд И. М. Лекции по линейной алгебре. 5-е изд. — М.: Добросвет, МЦНМО, 1998. — 320 с. — ISBN 5-7913-0016-6.
Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. 2-е изд. — М.: Наука, 1986. — 304 с.
Кострикин А. И. Введение в алгебру. Ч. 2: Линейная алгебра. — 3-е. — М.: Наука., 2004. — 368 с. — (Университетский учебник).
Мальцев А. И. Основы линейной алгебры. — 3-е. — М.: Наука, 1970. — 400 с.

Постников М. М. Линейная алгебра (Лекции по геометрии. Семестр II). — 2-е. — М.: Наука, 1986. — 400 с.
Стренг Г. Линейная алгебра и её применения = Linear Algebra and Its Applications. — М.: Мир, 1980. — 454 с.
Ильин В. А., Позняк Э. Г. Линейная алгебра. 6-е изд. — М.: Физматлит, 2010. — 280 с. — ISBN 978-5-9221-0481-4.
Халмош П. Конечномерные векторные пространства = Finite-Dimensional Vector Spaces. — М.: Физматгиз, 1963. — 263 с.
Фаддеев Д. К. Лекции по алгебре. — 5-е. — СПб.: Лань, 2007. — 416 с.
Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — 1-е. — М.: Физматлит, 2009. — 511 с.
Шрейер О., Шпернер Г. Введение в линейную алгебру в геометрическом изложении = Einfuhrung in die analytische Geometrie und Algebra / Ольшанский Г. (перевод с немецкого). — М.—Л.: ОНТИ, 1934. — 210 с.

[1] Не следует путать понятия «умножение на скаляр» и «скалярное произведение».

[_f0e3fa2a83881c49-2] Ильин, Позняк, 2010, с. 45.

[_2fd5354e095ac89c-3] Кострикин, Манин, 1986, с. 8.

[_a7b013809090145a-4] Кострикин, Манин, 1986, с. 198.

[_a2122899e542d519-5] Кострикин, Манин, 1986, с. 16.

[_a2122899e542d51b-6] Кострикин, Манин, 1986, с. 14.

[7] Шилов Г. Е. Введение в теорию линейных пространств. — М., Л., Гостехтеориздат, 1952. — с. 70

[1]

[2]

[3]

[4]

[5]

[6]

[7]