Умножение матриц
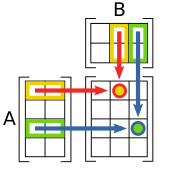
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц. Элементы новой матрицы получаются из элементов старых матриц в соответствии с правилами, проиллюстрированными ниже.
Матрицы [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] могут быть перемножены, если они совместимы в том смысле, что число столбцов матрицы [math]\displaystyle{ A }[/math] равно числу строк [math]\displaystyle{ B }[/math].
Матрицы обладают многими алгебраическими свойствами умножения, присущими обычным числам, за исключением коммутативности.
Для квадратных матриц, помимо умножения, может быть введена операция возведения матрицы в степень и обратная матрица.
Тогда как матрицы используются для описания, в частности, преобразований математических пространств (поворот, отражение, растяжение и другие), произведение матриц будет описывать композицию преобразований.
Определение
Пусть даны две прямоугольные матрицы [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] размерности [math]\displaystyle{ l \times m }[/math] и [math]\displaystyle{ m \times n }[/math] соответственно:
- [math]\displaystyle{ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{l1} & a_{l2} & \cdots & a_{lm} \end{bmatrix},\;\;\; B = \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \end{bmatrix}. }[/math]
Тогда матрица [math]\displaystyle{ C }[/math] размерностью [math]\displaystyle{ l \times n }[/math]:
- [math]\displaystyle{ C = \begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{l1} & c_{l2} & \cdots & c_{ln} \end{bmatrix}, }[/math]
в которой:
- [math]\displaystyle{ c_{ij} = \sum_{r=1}^m a_{ir}b_{rj} \;\;\; \left(i=1, 2, \ldots l;\; j=1, 2, \ldots n \right). }[/math]
называется их произведением.
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что матрицы согласованы. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Таким образом, из существования произведения [math]\displaystyle{ AB }[/math] вовсе не следует существование произведения [math]\displaystyle{ BA. }[/math]
Иллюстрация
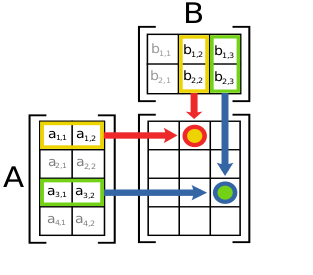
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений вектор-строк матрицы A и вектор-столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой вектор-строки матрицы A и j-го вектор-столбца матрицы B.
Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.
Значения на пересечениях, отмеченных кружочками, будут:
[math]\displaystyle{ \begin{align} {\color{Red}x_{1,2}} &= (a_{1,1}, a_{1,2})\cdot(b_{1,2}, b_{2,2}) \\ &= a_{1,1}b_{1,2} + a_{1,2}b_{2,2} \\ {\color{Blue}x_{3,3}} &= (a_{3,1}, a_{3,2})\cdot(b_{1,3}, b_{2,3}) \\ &= a_{3,1}b_{1,3} + a_{3,2}b_{2,3} \end{align} }[/math]
В общем случае, произведение матриц не является коммутативной операцией. К примеру:
- [math]\displaystyle{ \overset{3\times 4 \text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \color{Blue} 1 & \color{Blue} 2 & \color{Blue} 3 & \color{Blue} 4 \\ \end{bmatrix}} \overset{4\times 5\text{ matrix}}{\begin{bmatrix} \cdot & \cdot & \cdot & \color{Red}a & \cdot \\ \cdot & \cdot & \cdot & \color{Red}b & \cdot \\ \cdot & \cdot & \cdot & \color{Red}c & \cdot \\ \cdot & \cdot & \cdot & \color{Red}d & \cdot \\ \end{bmatrix}} = \overset{3\times 5\text{ matrix}}{ \begin{bmatrix} \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & x_{3,4} & \cdot \\ \end{bmatrix}} }[/math]
Элемент [math]\displaystyle{ x_{3,4} }[/math] произведения матриц, приведённых выше, вычисляется следующим образом
- [math]\displaystyle{ x_{3,4} = ({\color{Blue}1}, {\color{Blue}2}, {\color{Blue}3}, {\color{Blue}4})\cdot ({\color{Red}a}, {\color{Red}b}, {\color{Red}c}, {\color{Red}d}) = {\color{Blue} 1}\cdot{\color{Red} a} +{\color{Blue} 2}\cdot{\color{Red} b} +{\color{Blue} 3}\cdot{\color{Red} c} +{\color{Blue} 4}\cdot{\color{Red} d} }[/math]
Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент [math]\displaystyle{ x_{{\color{Blue}i}{\color{Red}j}} }[/math] на пересечении строки [math]\displaystyle{ i }[/math] и столбца [math]\displaystyle{ j }[/math] результирующей матрицы является скалярным произведением [math]\displaystyle{ i }[/math]-й строки первой матрицы и [math]\displaystyle{ j }[/math]-го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Обсуждение
Увидеть причины описанного правила матричного умножения легче всего, рассмотрев умножение вектора на матрицу.
Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A даёт выражение компонент вектора v' = Av:
- [math]\displaystyle{ v'_i = \sum\limits_j A_{ij} v_j }[/math]
То есть линейный оператор оказывается представлен матрицей, векторы — векторами-столбцами, а действие оператора на вектор — матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц — вектор-столбец — имеет размер [math]\displaystyle{ n\times 1 }[/math]).
(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только [math]\displaystyle{ v'_i }[/math] в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом [math]\displaystyle{ A_{ij} }[/math] — элементы матрицы перехода к новому базису).
Рассмотрев последовательное действие на вектор двух операторов: сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), дважды применив нашу формулу, получим:
- [math]\displaystyle{ v''_i = \sum\limits_j B_{ij}\sum\limits_k A_{jk} v_k = \sum\limits_j \sum\limits_k B_{ij} A_{jk} v_k = \sum\limits_k \sum\limits_j (B_{ij} A_{jk}) v_k, }[/math]
откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по правилу произведения соответствующих матриц:
- [math]\displaystyle{ (BA)_{ik} = \sum\limits_j B_{ij} A_{jk}. }[/math]
Определённое таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (даёт простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).
Свойства
Сочетательное свойство, ассоциативность:
- [math]\displaystyle{ \mathbf{A} ( \mathbf{B C} ) = ( \mathbf{A B} ) \mathbf{C}; }[/math]
- [math]\displaystyle{ \alpha (\mathbf{AB}) = (\alpha\mathbf{A}) \mathbf{B} = \mathbf{A}(\alpha\mathbf{B}). }[/math]
Распределительное свойство, дистрибутивность относительно сложения:
- [math]\displaystyle{ \mathbf{A} ( \mathbf{B} + \mathbf{C} ) = \mathbf{A B} + \mathbf{AC}; }[/math]
- [math]\displaystyle{ ( \mathbf{A} + \mathbf{B} ) \mathbf{C} = \mathbf{A C} + \mathbf{B C}. }[/math].
Произведение матрицы на единичную матрицу [math]\displaystyle{ \mathbf{E} }[/math] подходящего порядка равно самой матрице:
- [math]\displaystyle{ \mathbf{EA} = \mathbf{A}; }[/math]
- [math]\displaystyle{ \mathbf{AE} = \mathbf{A}. }[/math]
Произведение матрицы на нулевую матрицу [math]\displaystyle{ \mathbf{0} }[/math] подходящей размерности равно нулевой матрице:
- [math]\displaystyle{ \mathbf{0A} = \mathbf{0}; }[/math]
- [math]\displaystyle{ \mathbf{A0} = \mathbf{0}. }[/math]
Если [math]\displaystyle{ \mathbf{A} }[/math] и [math]\displaystyle{ \mathbf{B} }[/math] — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
Умножение матриц в общем случае некоммутативно:
- [math]\displaystyle{ \mathbf{AB} \ne \mathbf{BA}. }[/math]
Если [math]\displaystyle{ \mathbf{AB} = \mathbf{BA} }[/math], то матрицы [math]\displaystyle{ \mathbf{A} }[/math] и [math]\displaystyle{ \mathbf{B} }[/math] называются коммутирующими между собой.
Простейшие примеры коммутирующих матриц:
- любая квадратная матрица — с самой собой: [math]\displaystyle{ \mathbf{AA} = \mathbf{AA} = \mathbf{A^2} }[/math] (возведение матрицы в квадрат);
- любая квадратная матрица — с единичной матрицей того же порядка: [math]\displaystyle{ \mathbf{AE} = \mathbf{EA} = \mathbf{A} }[/math];
- любая квадратная матрица — с нулевой матрицей того же порядка: [math]\displaystyle{ \mathbf{A0} = \mathbf{0A} = \mathbf{0} }[/math];
- любая невырожденная квадратная матрица — со своей обратной матрицей: [math]\displaystyle{ \mathbf{AA^{-1}} = \mathbf{A^{-1}A} = \mathbf{E} }[/math].
Определитель и след произведения не зависят от порядка умножения матриц:
- [math]\displaystyle{ \det(\mathbf{AB}) = \det(\mathbf{BA}) = \det \mathbf{A} \cdot \det\mathbf{B}; }[/math]
- [math]\displaystyle{ \mbox{tr}(\mathbf{AB}) = \mbox{tr}(\mathbf{BA}). }[/math]
Обратная матрица
Квадратная матрица [math]\displaystyle{ A }[/math] называется неособенной (невырожденной), если она имеет единственную обратную матрицу [math]\displaystyle{ A^{-1} }[/math] такую, что выполняется условие:
- [math]\displaystyle{ AA^{-1} = A^{-1}A = E. }[/math]
В противном случае матрица [math]\displaystyle{ A }[/math] называется особенной (вырожденной).
Матрица [math]\displaystyle{ A = \left [ a_{ik} \right] }[/math] порядка [math]\displaystyle{ n }[/math] является невырожденной в том и только в том случае, если [math]\displaystyle{ \det A = \det \left [ a_{ik} \right ] \ne 0; }[/math] в этом случае [math]\displaystyle{ A^{-1} }[/math] есть квадратная матрица того же порядка [math]\displaystyle{ n: }[/math]
- [math]\displaystyle{ A^{-1} = \left [ a_{ik} \right ]^{-1} = \left [ \frac{A_{ki}}{\det A} \right ], }[/math]
где [math]\displaystyle{ A_{ik} }[/math] — алгебраическое дополнение элемента [math]\displaystyle{ a_{ik} }[/math] в определителе [math]\displaystyle{ \det \left [ a_{ik} \right ]. }[/math]
Алгоритмы быстрого перемножения матриц
Сложность вычисления произведения матриц по определению составляет [math]\displaystyle{ \ O(n^3) }[/math], однако существуют более эффективные алгоритмы[1], применяющиеся для больших матриц. Вопрос о предельной скорости умножения больших матриц, также как и вопрос о построении наиболее быстрых и устойчивых практических алгоритмов умножения больших матриц остаётся одной из нерешённых проблем линейной алгебры.
- Алгоритм Штрассена (1969)
- Первый алгоритм быстрого умножения больших матриц был разработан Фолькером ШтрассеномШаблон:Source-ref в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки 2Х2. Штрассен доказал, что матрицы 2Х2 можно некоммутативно перемножить с помощью семи умножений, поэтому на каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате асимптотическая сложность этого алгоритма составляет [math]\displaystyle{ O( n^{\log_{2}7}) \approx O(n^{2.81}) }[/math]. Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, слабая численная устойчивость и больший объём используемой памяти. Разработан ряд алгоритмов на основе метода Штрассена, которые улучшают численную устойчивость, скорость по константе и другие его характеристики. Тем не менее, в силу простоты алгоритм Штрассена остаётся одним из практических алгоритмов умножения больших матриц. Штрассен также выдвинул следующую гипотезу Штрассена: для сколь угодно малого [math]\displaystyle{ \varepsilon \gt 0 }[/math] существует алгоритм, при достаточно больших натуральных n гарантирующий перемножение двух матриц размера [math]\displaystyle{ n \times n }[/math] за [math]\displaystyle{ O(n^{2+\varepsilon}) }[/math] операций.
- Дальнейшие улучшения показателя степени ω для скорости матричного умножения
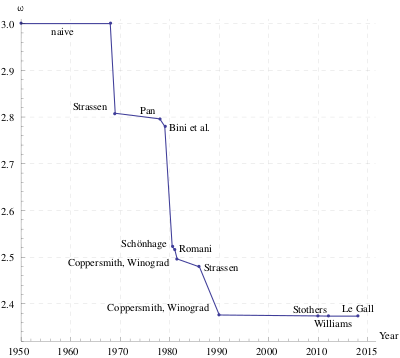
- В дальнейшем оценки скорости умножения больших матриц многократно улучшались. Однако эти алгоритмы носили теоретический, в основном приближённый характер. В силу неустойчивости алгоритмов приближённого умножения в настоящее время они не используются на практике.
- Алгоритм Пана (1978)
- В 1978 Пан[2] предложил свой метод умножения матриц, сложность которого составила Θ(n2.78041).
- Алгоритм Бини (1979)
- В 1979 группа итальянских учёных во главе с Бини[3] разработала алгоритм умножения матриц с использованием тензоров. Его сложность составляет Θ(n2.7799).
- Алгоритмы Шёнхаге (1981)
- В 1981 Шёнхаге[4] представил метод, работающий со скоростью Θ(n2.695). Оценка получена с помощью подхода, названного частичным матричным умножением. Позже ему удалось получить оценку Θ(n2.6087).
- Затем Шёнхаге на базе метода прямых сумм получил оценку сложности Θ(n2.548). Романи сумел понизить оценку до Θ(n2.5166), а Пан — до Θ(n2.5161).
- В 1990 Копперсмит и Виноград[5] опубликовали алгоритм, который в модификации Вильямс Василевской[6] 2011 года умножает матрицы со скоростью O(n2.3727). Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день модификации алгоритма Копперсмита-Винограда являются наиболее асимптотически быстрыми. Но тот факт, что полученные улучшения ничтожны, позволяет говорить о существовании «барьера Копперсмита-Винограда» в асимптотических оценках скорости алгоритмов. Алгоритм Копперсмита-Винограда эффективен только на матрицах астрономического размера и на практике применяться не может.
- Связь с теорией групп (2003)
- В 2003 Кох и др. рассмотрели в своих работах[7] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали, что гипотеза Штрассена справедлива (т.е. минимальная сложность ограничена [math]\displaystyle{ O(n^{2+\epsilon}) }[/math] для любого [math]\displaystyle{ \epsilon }[/math]) , если выполняется одна из гипотез теории групп[8].
Степени матриц
Квадратные матрицы можно многократно умножать сами на себя так же, как обычные числа, так как у них одинаковое число строк и столбцов. Такое последовательное умножение можно назвать возведением матрицы в степень — это будет частный случай обычного умножения нескольких матриц. У прямоугольных матриц число строк и столбцов разное, поэтому их никогда нельзя возводить в степень. Матрица A размерности n × n, возведённая в степень, определяется формулой
- [math]\displaystyle{ \mathbf{A}^k = \underbrace{\mathbf{A}\mathbf{A}\cdots\mathbf{A}}_{k} }[/math]
и обладает следующими свойствами (λ — некоторый скаляр):
Нулевая степень:
- [math]\displaystyle{ \mathbf{A}^0 = \mathbf{E} }[/math]
где E - единичная матрица. Это аналог того факта, что нулевая степень любого числа равна единице.
Умножение на скаляр:
- [math]\displaystyle{ ( \lambda \mathbf{A} )^k = \lambda^k\mathbf{A}^k }[/math]
Определитель:
- [math]\displaystyle{ \det(\mathbf{A}^k) = \det(\mathbf{A})^k }[/math]
Наиболее простой способ вычисления степени матрицы — это умножать k раз матрицу A на результат предыдущего умножения, начиная с единичной матрицы, как это часто делают для скаляров. Для диагонализируемых матриц существует лучший метод, основанный на использовании спектрального разложения матрицы A. Ещё один метод, основанный на теореме Гамильтона — Кэли, строит более эффективное выражение для Ak, в котором в требуемую степень возводится скаляр, а не вся матрица.
Особый случай составляют диагональные матрицы. Так как произведение диагональных матриц сводится к умножению соответствующих диагональных элементов, то k-ая степень диагональной матрицы A состоит из элементов, возведённых в требуемую степень:
- [math]\displaystyle{ \mathbf{A}^k = \begin{pmatrix} a_{11} & 0 & \cdots & 0 \\ 0 & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \end{pmatrix}^k = \begin{pmatrix} a_{11}^k & 0 & \cdots & 0 \\ 0 & a_{22}^k & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn}^k \end{pmatrix}. }[/math]
Таким образом, возвести диагональную матрицу в степень несложно. При возведении произвольной матрицы (не обязательно диагональной) в степень часто полезным оказывается использовать сначала свойства диагонализируемых матриц.
Используя умножение матриц и возведение матриц в степень, можно определить другие операции над матрицами. Например, матричная экспонента может быть определена через степенной ряд, матричный логарифм — как обратная к матричной экспоненте функция и так далее.
См. также
Литература
- Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 392—394.
Примечания
- ↑ Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983 — 1985 гг.: Пер. с англ. — М.: Мир, 1988 — В.Б. Алекссев. Сложность умножения матриц. Обзор.
- ↑ Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations. — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
- ↑ Bini D., Capovani M., Lotti G., Romani F. — [math]\displaystyle{ O( n^{2.7799} ) }[/math] complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
- ↑ Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251-280, 1990.
- ↑ Williams, Virginia (2011), Multiplying matices in O(n2.3727 time Архивная копия от 26 октября 2014 на Wayback Machine
- ↑ Group-theoretic Algorithms for Matrix Multiplication. Дата обращения: 26 сентября 2009. Архивировано 6 августа 2011 года.
- ↑ Toward an Optimal Algorithm for Matrix Multiplication (недоступная ссылка). Дата обращения: 26 сентября 2009. Архивировано 31 марта 2010 года.