Поворот

Поворот фигуры в плоскости относительно точки O против часовой стрелки на угол α

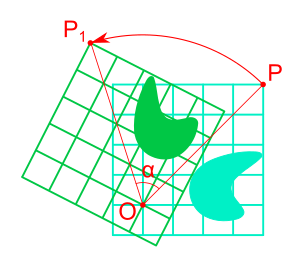
Поворо́т (враще́ние) — движение плоскости или пространства, при котором по крайней мере одна точка остаётся неподвижной.

Связанные определения

• Неподвижная точка при повороте плоскости называется центром вращения.
• Неподвижная прямая при повороте трёхмерного пространства называется осью вращения.

Собственное и несобственное вращения

Определения

• Вращение называется собственным, если оно сохраняет ориентацию пространства.

• Возможно ещё одно определение собственного вращения для плоскости: собственное вращение плоскости — это движение, при котором все лучи, исходящие из данной точки, поворачиваются на один и тот же угол в одном и том же направлении (по или против часовой стрелки).

• Вращение называется несобственным, если оно не является собственным.

Часто под термином вращение подразумевается только собственное вращение.

Свойства

• Несобственное вращение является композицией некоторого собственного вращения и зеркального отражения (на плоскости — осевой симметрии, в пространстве нечётной размерности — центральной).

• Для любой ограниченной области пространства его собственное вращение относительно любой точки можно сделать таким, чтобы все точки области сместились не более, чем на некоторое заранее фиксированное расстояние, однако для несобственного вращения данное утверждение перестаёт быть верным.

Поворот в двумерном пространстве

В аналитической геометрии на плоскости собственное вращение в прямоугольных декартовых координатах выражается формулами:

[math]\displaystyle{ x'=x\cos\varphi-y\sin\varphi, }[/math]

[math]\displaystyle{ y'=x\sin\varphi+y\cos\varphi, }[/math]

где [math]\displaystyle{ \varphi }[/math] — угол поворота, а центр вращения выбран в начале координат.
При тех же условиях несобственное вращение плоскости выражается формулой

[math]\displaystyle{ x'=x\cos\varphi+y\sin\varphi, }[/math]

[math]\displaystyle{ y'=x\sin\varphi-y\cos\varphi. }[/math]

В планиметрии поворот около точки [центра] [math]\displaystyle{ O }[/math] на угол поворота [math]\displaystyle{ \alpha }[/math] обозначается также [math]\displaystyle{ R^{\alpha}_{O} }[/math], где [math]\displaystyle{ \alpha \in ( -\pi; \pi ]. }[/math]
Поворот на угол [math]\displaystyle{ \beta' = \alpha + 2 \pi \cdot n , }[/math] где [math]\displaystyle{ n \in \Z }[/math] и [math]\displaystyle{ \alpha \in ( -\pi; \pi ] }[/math] отождествляется с поворотом [math]\displaystyle{ R^{\alpha}_{O} }[/math] (угол поворота на полный угол [math]\displaystyle{ 2 \pi ~ (360^\circ) }[/math] зачастую также называется оборотом).
Если углы поворотов [math]\displaystyle{ \alpha, \beta }[/math] и их сумма [math]\displaystyle{ \alpha + \beta }[/math] заключены в пределах от [math]\displaystyle{ - \pi }[/math] до [math]\displaystyle{ \pi , }[/math] то при последовательном выполнении (композиции) поворотов их углы складываются (см. также #Композиция поворотов на плоскости (комплексный вид)):

[math]\displaystyle{ R^{\beta}_{O} \circ R^{\alpha}_{O} = R^{\alpha+\beta}_{O} , }[/math]

причём композиция двух поворотов обладает свойством коммутативности:

[math]\displaystyle{ R^{\beta}_{O} \circ R^{\alpha}_{O} = R^{\alpha}_{O} \circ R^{\beta}_{O}. }[/math]

См. также Изометрия (математика)

Матричный вид

При использовании матричного подхода точку [math]\displaystyle{ (x, y) }[/math] записывают в виде вектора, затем умножают на матрицу:

[math]\displaystyle{ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} }[/math].

[math]\displaystyle{ (x ', y') }[/math] координаты точки, полученные вращением точки [math]\displaystyle{ (x , y) }[/math].

Векторы [math]\displaystyle{ \begin{bmatrix} x \\ y \end{bmatrix} }[/math] и [math]\displaystyle{ \begin{bmatrix} x' \\ y' \end{bmatrix} }[/math] имеют одинаковую размерность.

Комплексный вид

Вращение плоскости можно представить с помощью комплексных чисел. Множество всех этих чисел геометрически представляет собой двумерную комплексную плоскость. Точка [math]\displaystyle{ (x, y) }[/math] на плоскости представлена комплексным числом [math]\displaystyle{ z = x + iy }[/math].

Вращение точки на угол [math]\displaystyle{ \theta }[/math] можно осуществить умножением [math]\displaystyle{ e ^ {i \theta} }[/math], используя формулу Эйлера

[math]\displaystyle{ \begin{align} e^{i \theta} z &= (\cos \theta + i \sin \theta) (x + i y) \\ &= (x \cos \theta + i y \cos \theta + i x \sin \theta - y \sin \theta) \\ &= (x \cos \theta - y \sin \theta) + i (x \sin \theta + y \cos \theta) \\ &= x' + i y' , \end{align} }[/math]

что дает такой же результат,

[math]\displaystyle{ \begin{align} x'&=x\cos\theta-y\sin\theta\\ y'&=x\sin\theta+y\cos\theta. \end{align} }[/math]

Композиция поворотов на плоскости (комплексный вид)

Пусть совершается вначале поворот вокруг точки [math]\displaystyle{ a }[/math] на угол [math]\displaystyle{ \alpha }[/math], затем поворот вокруг точки [math]\displaystyle{ b }[/math] на угол [math]\displaystyle{ \beta }[/math]. И пусть точки [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] представлены в виде комплексных чисел вида [math]\displaystyle{ x + i y }[/math]. Положительным считается поворот против часовой стрелки. Такая композиция поворотов эквивалентна повороту на угол [math]\displaystyle{ \gamma~= \alpha + \beta }[/math] вокруг точки [math]\displaystyle{ c }[/math], которая вычисляется по формуле [math]\displaystyle{ c = a + (b-a) e^{i {\alpha'}}\frac {\sin \alpha'}{\sin \gamma'} }[/math],

где [math]\displaystyle{ \alpha' = \frac \alpha 2 }[/math], а [math]\displaystyle{ \gamma' = \frac \gamma 2 }[/math]

Если [math]\displaystyle{ \alpha + \beta = 0 }[/math], то композиция поворотов эквивалентна параллельному сдвигу плоскости на вектор [math]\displaystyle{ r = (b - a)(e^{i \alpha} - 1) }[/math]

Свойства

• Если репер привязан к центру вращения, то оно реализуется ортогональной матрицей.
  • Вращения трёхмерного евклидова пространства (с фиксированным центром) образуют группу O(3) (собственные — группу SO(3)).
  • Вращения двумерного пространства (плоскости) образуют соответственно группы O(2) и SO(2) (изоморфную U(1)).

См. также

• Вращательное движение — процесс непрерывного поворота в механике.
• Группа вращений
• Матрица поворота
• Ортогональная группа
• Ортогональное преобразование
• Специальная ортогональная группа
• Угловая скорость